A wavelet is a kind of mathematical function used to divide a given function or continuous-time signal into different frequency components and study each component with a resolution that matches its scale. A wavelet transform is the representation of a function by wavelets. The wavelets are scaled and translated copies (known as "daughter wavelets") of a finite-length or fast-decaying oscillating waveform (known as the "mother wavelet"). Wavelet transforms have advantages over traditional Fourier transforms for representing functions that have discontinuities and sharp peaks, and for accurately deconstructing and reconstructing finite, non-periodic and/or non-stationary signals.

     In formal terms, this representation is a wavelet series representation of a square-integrable function with respect to either a complete, orthonormal set of basis functions, or an overcomplete set of Frame of a vector space (also known as a Riesz basis), for the Hilbert space of square integrable functions.

     Wavelet transforms are classified into discrete wavelet transforms (DWTs) and continuous wavelet transforms (CWTs). Note that both DWT and CWT are of continuous-time (analog) transforms. They can be used to represent continuous-time (analog) signals. CWTs operate over every possible scale and translation whereas DWTs use a specific subset of scale and translation values or representation grid. The word wavelet is due to Morlet and Grossmann in the early 1980s. They used the French word ondelette, meaning "small wave". Soon it was transferred to English by translating "onde" into "wave", giving "wavelet".

      Wavelet theory is applicable to several subjects. All wavelet transforms may be considered forms of time-frequency representation for continuous-time (analog) signals and so are related to harmonic analysis. Almost all practically useful discrete wavelet transforms use discrete-time filterbanks. These filter banks are called the wavelet and scaling coefficients in wavelets nomenclature. These filterbanks may contain either finite impulse response (FIR) or infinite impulse response (IIR) filters. The wavelets forming a CWT are subject to the uncertainty principle of Fourier analysis respective sampling theory: Given a signal with some event in it, one cannot assign simultaneously an exact time and frequency resp. scale to that event. The product of the uncertainties of time and frequency resp. scale has a lower bound. Thus, in the scaleogram of a continuous wavelet transform of this signal, such an event marks an entire region in the time-scale plane, instead of just one point. This is related to Heisenberg's uncertainty principle of quantum physics and has a similar derivation. Also, discrete wavelet bases may be considered in the context of other forms of the uncertainty principle.

      In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. The first DWT was invented by the Hungarian mathematician Alfr?d Haar. For an input represented by a list of 2n numbers, the Haar wavelet transform may be considered to simply pair up input values, storing the difference and passing the sum. This process is repeated recursively, pairing up the sums to provide the next scale: finally resulting in 2n ? 1 differences and one final sum. This simple DWT illustrates the desirable properties of wavelets in general. First, it can be performed in O(n) operations; second, it captures not only a notion of the frequency content of the input, by examining it at different scales, but also temporal content, i.e. the times at which these frequencies occur. Combined, these two properties make the Fast wavelet transform (FWT), an alternative to the conventional Fast Fourier Transform (FFT).

     The most commonly used set of discrete wavelet transforms was formulated by the Belgian mathematician Ingrid Daubechies in 1988. This formulation is based on the use of recurrence relations to generate progressively finer discrete samplings of an implicit mother wavelet function; each resolution is twice that of the previous scale. In her seminal paper, Daubechies derives a family of wavelets, the first of which is the Haar wavelet. Interest in this field has exploded since then, and many variations of Daubechies' original wavelets were developed.

     Other forms of discrete wavelet transform include the non- or undecimated wavelet transform (where downsampling is omitted), the Newland transform (where an orthonormal basis of wavelets is formed from appropriately constructed top-hat filters in frequency space). Wavelet packet transforms are also related to the discrete wavelet transform. Complex wavelet transform is another form. The discrete wavelet transform has a huge number of applications in science, engineering, mathematics and computer science. Most notably, it is used for signal coding, to represent a discrete signal in a more redundant form, often as a preconditioning for data compression. The discrete wavelet transform has a huge number of applications in science, engineering, mathematics and computer science. Most notably, it is used for signal coding, to represent a discrete signal in a more redundant form, often as a preconditioning for data compression.

      A continuous wavelet transform is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization. In mathematics, the continuous wavelet transform of a continuous, square-integrable function x(t) is expressed by the following integraliscarding every other sample. This constitutes one level of decomposition and can mathematically be expressed as follows. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization. In mathematics, the continuous wavelet transform of a continuous, square-integrable function x(t) is expressed by the following integral

     where ?(t) is a continuous function in both the time domain and the frequency domain called the mother wavelet, b is the translation factor and a is the scale factor. The main purpose of the mother wavelet is to provide a source function to generate the daughter wavelets which are simply the translated and scaled versions of the mother wavelet. To recover the original signal x(t), inverse continuous wavelet transform can be exploited.

     Some example mother wavelets are:

     f(t)is the dual function of ps(t). And the dual function should satisfy

     It should also be noted that the criterion of admissibility implies that Ps (0) = 0, so that the integral of wavelet should be zero. Wavelet-parent (mother wavelet) relates to the wavelet-descendant (daughter wavelet) follows:

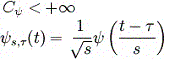
     One of the most popular applications of wavelet transform is image compression. The advantage of using wavelet-based coding in image compression is that it provides significant improvements in picture quality at higher compression ratios over conventional techniques. Since wavelet transform has the ability to decompose complex information and patterns into elementary forms, it is commonly used in acoustics processing and pattern recognition. Moreover, wavelet transforms can be applied to the following scientific research areas: edge and corner detection, partial differential equation solving, transient detection, filter design, Electrocardiogram (ECG) analysis, texture analysis and business information analysis.