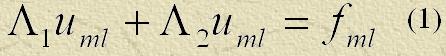
У цей час однієї зі складних завдань у світі вважається рішення ресурсномістких завдань. Якщо виникає необхідність у рішенні складної обчислювальної проблеми, наприклад, рішення системи з 1000 рівнянь, проведенні пов'язаних з нею розрахунків, порівнянь і сортувань, то ні кластери балансування навантаження, ні кластери високої доступності тут не допоможуть. Для рішення подібних ресурсномістких завдань застосовується окремий тип кластерів, що називають обчислювальним або академічним.
Обчислювальні кластери (High Performance Computing Cluster) забезпечують підвищення продуктивності цільових додатків, якщо функції цих додатків — ресурсномісткі обчислення. Ріст продуктивності прямо пов'язаний з розподілом одного обчислювального процесу по всіх доступних вузлах кластера.
Свою версію кластера в 2005 році випустила компанія Microsoft. Цей продукт одержав назву Microsoft Windows Compute Cluster Server 2003 (WCCS 2003).Технологічно Microsoft Windows Compute Cluster Server 2003 [8] базується на стандартній версії Microsoft Windows Server 2003. У поставку продукту входять: модифікована версія Windows Server 2003 x64 Standard Edition і пакет, називаний Compute Cluster Pack.
Модифікована версія Windows Server 2003 дозволяє істотно знизити вартість кінцевого вузла, оскільки обмежує можливість роботи тільки в ролі вузла обчислювального кластера. Компоненти, що входять в Compute Cluster Pack [8], - це набір сервисов, утиліт і протоколів. Цей набір являє собою роль «обчислювальний кластер» для установки на базову операційну систему. Для спеціально розроблених обчислювальних завдань користувачі можуть застосовувати стандартну поставку WCCS 2003.
Убудованим засобом програмування на кластері є MS MPI. Message Passing Interface (MPI) - один зі стандартів розробки додатків HPC.
У завдання MPI входить створення набору процесів й їхніх сесій, забезпечення передачі даних і сигналів між ними для поділу коду додатка на потоки відповідно до наявних обчислювальних ресурсів з метою досягнення максимальної продуктивності.
Дослідження паралельного багатосіткового методу Федоренко на обчислювальному кластері Microsoft Windows Compute Cluster Server 2003 актуально, тому що такі дослідження ще не проводилися.
Метою роботи є розробка й реалізація програмної системи, що дозволяє одержати рішення диференціальних рівнянь у частинних похідних багатосіткових методом на обчислювальному кластері.
Головними завданнями досліджень є:
Предметом досліджень є технології паралельного рішення рівнянь у частинних похідних на обчислювальному кластері Microsoft Windows Compute Cluster Server 2003 із застосуванням багатосіткових методів.
Дані дослідження виконуються вперше в зазначених умовах.
Використання програмної системи дозволить оцінити швидкодія й точність рішення диференціальних рівнянь паралельним методом на обчислювальному кластері. Програмна система може бути використана для паралельного рішення диференціальних рівнянь у частинних похідних багатосітковим методом.
За результатами виконаних досліджень автором зроблений доповідь, на міжнародній науково-технічній конференції "Інформатика й комп'ютерні технології" 12-15 травня 2009 відбулася в м. Донецьку в стінах Донецького Національного Технічного Університету
Диференціальні рівняння в частинних похідних являють собою широко застосовуваний математичний апарат при розробці моделей у самих різних галузях науки й техніки.
Як відомо, явне рішення цих рівнянь в аналітичному виді виявляється можливим тільки в приватних простих випадках. Тому основна можливість аналізу математичних моделей, побудованих на основі диференціальних рівнянь, забезпечуються за допомогою наближених чисельних методів рішення. Обсяг виконуваних при цьому обчислень є значним. Тому необхідним є використання високопродуктивних обчислювальних систем для даної області обчислювальної математики. У цей час проблематика чисельного рішення диференціальних рівнянь у частинних похідних є предметом інтенсивних досліджень.
Одним з найбільш ефективних підходів до рішення диференціальних рівнянь у частинних похідних є багатосітковий підхід. Головною особливістю є те, що рішення виробляється спочатку на грубій(великої) сітці, а потім переноситься на більше дрібну сітку. Початкове рішення для сітки Nx, де N - кількість вузлів, будується за допомогою апроксимуючої сітки (N/2)x(N/2), одержуваної збереженням кожного другого вузла вихідної сітки Nx. Більше груба сітка (N/2)х(N/2), у свою чергу, апроксимується сіткою (N/4)х(N/4) і так далі. Потім у приватній області погрішність представляється як сума синусоїд з різними частотами. Тоді робота, виконувана на конкретній сітці, зменшує половину частотних компонентів погрішності, для яких зменшення не було досягнуто на більше грубих сітках. Тому робота, вироблена для усереднення рішення в кожному вузлі сітки, робить наближене рішення, що еквівалентно придушенню високочастотних компонентів погрішності.
Наближений алгоритм рішення розглянемо на сітковому рівнянні Пуассона:
Розглянемо сіткове рівняння Пуассона на п'ятиточковому шаблоні різницевої схеми "хрест"[10]:
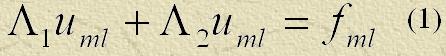
і, крім того, рівняння
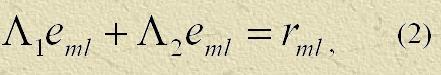
де
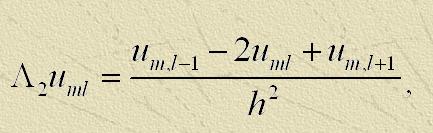
h – крок по координатах,
u – шукане рішення,
u' – наближене рішення (1),
r — нев'язання,
e — погрішність рішення.
Якщо відомо наближене рішення першого завдання, те, вирішуючи другу, можна знайти рішення вихідної системи по формулі,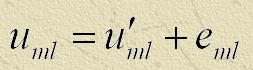 
,
але рішення завдання (2) по складності точно таке ж, як і рішення вихідного завдання.
Якщо застосовувати ітераційний метод до першого рівняння, зробивши кілька ітерацій, то наближене рішення завдання буде відомо, а нев'язання стане плавно мінливою функцією. Нев'язання буде добре представлятися на більше грубій сітці, тоді розмірність допоміжної системи другого рівняння понизяться.
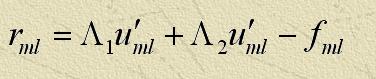
Приблизно так само буде й у загальному випадку. Здавалося б, конвеєрну обробку можна з успіхом замінити звичайним паралелізмом, для чого продублювати основний пристрій стільки разів, скільки щаблів конвеєра передбачається виділити. Однак вартість і складність системи, що вийшла, буде непорівнянна з вартістю й складністю конвеєрного варіанта, а продуктивність буде майже такий же.
Приклад реалізації багато сіткового методу на трьох сітках наведений на анімаційному малюнку 1.
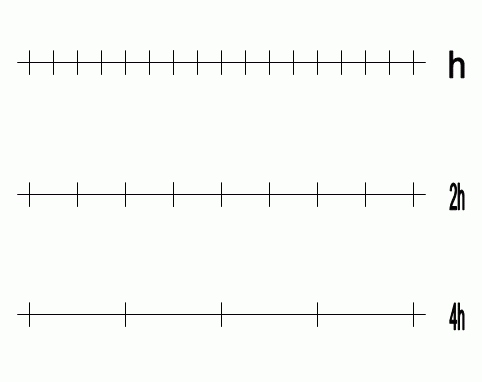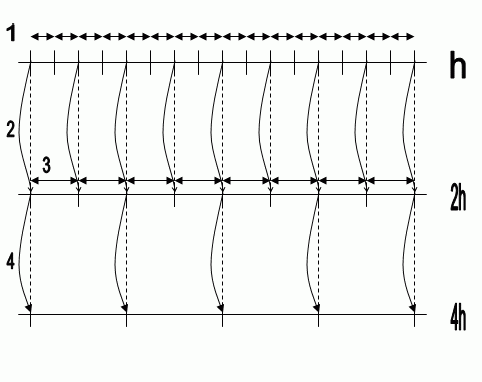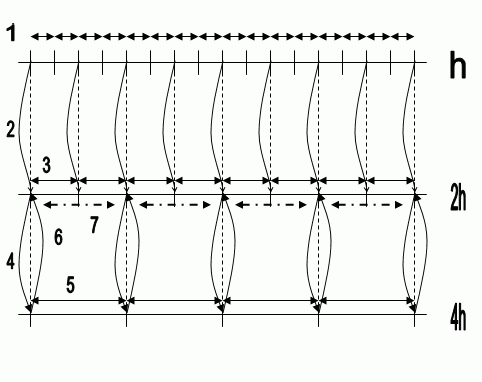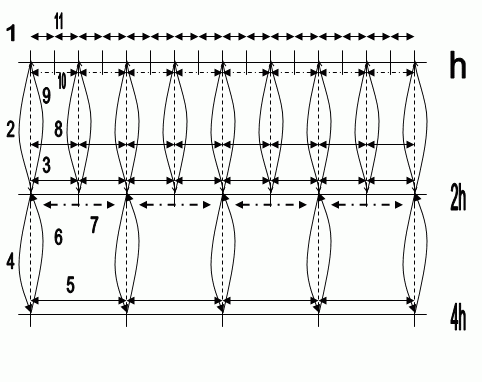
Позначення наведеного на анімованному малюнку приклада:
h – крок сітки(відстань між двома сусідніми вузлами).
- рішення отриманих рівнянь.
- інтерполяція отриманих значень на більше дрібну сітку.
- перенос, отриманих при рішенні, значень на більшу (дрібну) сітку.
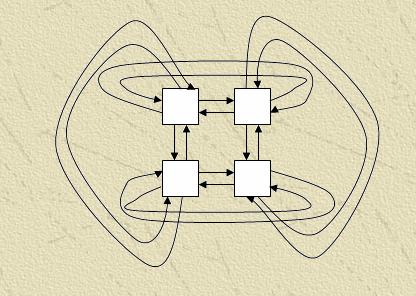
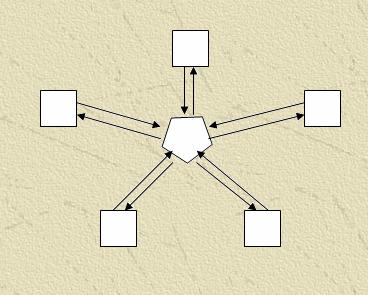
Для реалізації багатосіткових методів на обчислювальному кластері можна використати трохи типових топологий зв'язків:
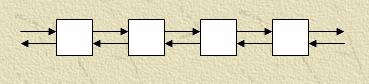
Модифікація - Кільце - з'єднані між собою кінцеві процесори.
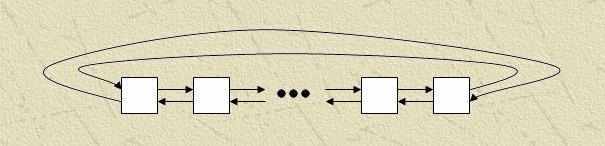
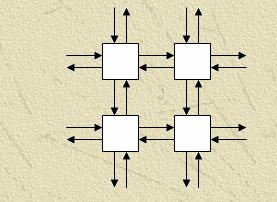
Модифікація - Замкнуті решітка – з'єднані між собою кінцеві процесори.
Для зручної реалізації програмної системи рішення багатосітковим методів необхідно використати об'єктно-ориєнтованний підхід. У даній програмній системі основними об'єктами будуть сіткові рівні, тобто кожна сітка - окремий об'єкт. Таке подання робить легенею реалізацію зв'язків у межах однієї сітки. А перехід від грубої сітки до більше докладного (або навпаки) буде можливий за рахунок того, що всі об'єкти є спадкоємцями одного класу, що містить повний опис об'єктів. Система містить кілька взаємозалежних підсистем. Підсистеми наведені на малюнку 7.
Підсистема уведення інформації - призначена для уведення інформації, необхідної для рішення.
Необхідно ввести:
Підсистема обробки даних:
Формуються структури, у яких будуть зберігається вихідні, проміжні й результуючі дані.
Підсистема паралельних обчислень:
Дана підсистема відповідає безпосередньо за реалізацію паралельного багатосіткового методу для рішення диференціальних рівнянь.
Підсистема балансування обчислювального навантаження припускає рівномірне навантаження обчислювальних вузлів. З появою нових завдань підсистема балансування повинна ухвалити рішення щодо тім, де (на якому обчислювальному вузлі) варто виконувати обчислення, пов'язані із цим новим завданням. Крім того, балансування припускає перенос частини обчислень із найбільш завантажених обчислювальних вузлів на менш завантажені вузли.
Підсистема виводу результатів - відповідає за зручне для вивчення подання отриманих результатів.
Необхідно вивести:
Така структура забезпечує керування даними, отриманими на кожній ітерації в процесі рішення завдання.
Використання програмної системи дозволить оцінити ефективність і точність паралельного рішення завдань у частинних похідних багатосітковим методом. Надалі при виконанні магістерської дисертації буде розроблена програмна система для рішення диференціальних рівнянь у частинних похідних. Реалізація паралельного багатосіткового методу дозволить провести експерименти розрахунку рівнянь у частинних похідних, що дозволить оцінити ефективність і точність вироблених обчислень.