
Щеглов Максим Игоревич
Факультет: Вычислительной техники и информатики
Специальность: Программное обеспечение автоматизированных систем
Тема магистерской диссертации: "Анализ и оценка эффективности параллельных многошаговых блочных методов решения ОДУ на кластере"
Научный руководитель: Фельдман Лев Петрович профессор, д.т.н.
Реферат
- Введение
- Актуальность темы
- Цель и задачи разработки и исследования
- Предмет разработки и исследования
- Практическое значение полученных результатов
- Параллельные многошаговые блочные методы численного решения задачи Коши для ОДУ
- Описание параллельных многошаговых блочных методов численного решения задачи Коши для ОДУ
- Погрешность аппроксимации блочных методов
- Оценка эффективности параллельных многошаговых блочных методов численного решения задачи Коши для ОДУ
- Выводы
- Список использованной литературы
Анализ и оценка эффективности параллельных многошаговых блочных методов решения ОДУ на кластере
Введение
Одним из самых важных направлений развития вычислительных технологий является распараллеливание вычислений. В последние годы максимальная производительность существующих параллельных вычислительных систем существенно выросла. Радикально изменилась технологическая база и архитектура. Но главным препятствием к внедрению практически всех параллельных архитектур является отсутствие параллельных алгоритмов. Приходится искать совершенно новые методы для решения различных задач, которые ориентированы на эффективное использование в многопроцессорных системах, или модернизировать существующие алгоритмы. Поскольку уже в ближайшем будущем перспективы развития суперЭВМ будут определяться успехами не столько электроники, сколько вычислительной математики.Речь, в первую очередь, идет об обычных дифференциальных уравнений и системах дифференциальных уравнений, которые являются основой современных научных и инженерных задач. Многие численные методы решения приходится пересматривать, а от некоторых полностью отказываться. В то же время, целый ряд вопросов, которые были несущественны или вообще не возникали при проведении последовательных вычислений, приобрели исключительную важность для эффективного и правильного использования вычислительных систем.
Опыт эксплуатации современных высокопроизводительных компьютерных систем показал, что эффективность их применения существенно зависит от согласования структуры параллельных вычислительных систем с классом решаемых задач и используемых численных методов. Эти обстоятельства послужили основой для адаптации известных и поиска новых методов решения систем обыкновенных дифференциальных уравнений на параллельных системах с MIMD архитектурой. Отсюда следует, что распараллеливание существующих и разработка новых параллельных алгоритмов является актуальной задачей.
В свою очередь при помощи дифференциальных уравнений и систем дифференциальных уравнений можно описать большое количество физических, механических, биологических, экономических и.т.п. явлений. Полученные модели, как правило, представляют собой дифференциальные уравнения, решение которых на однопроцессорных компьютерах за приемлемое время невозможно. Именно это привело к созданию параллельных методов решения задачи Коши.
Актуальность темы
При помощи дифференциальных уравнений и систем дифференциальных уравнений можно описать большое количество физических, механических, биологических, экономических и.т.п. явлений. Полученные модели, как правило, представляют собой дифференциальные уравнения, решение которых на однопроцессорных компьютерах за приемлемое время невозможно. Отсюда следует, что разработка параллельных методов решения задачи Коши является актуальной задачей.Цель и задачи разработки и исследования
Цель работы: анализ решения задачи Коши многошаговым параллельным блочным методом на вычислительном кластере, разработка и реализация программной системы, позволяющей получить решение данной задачи.Задачи: изучение многошаговых параллельных блочных методов решения задачи Коши, решение задачи Коши данными методами на вычислительном кластере с использованием Microsoft Visual Studio 2005 и технологии Message Passing Interface (MPI).
Предмет разработки и исследования
Предметом исследований являются параллельные блочные методы решения задачи Коши на вычислительном кластере Microsoft Windows Compute Cluster Server 2003.Практическое значение полученных результатов
Полученные результаты дадут возможность оценить эффективность параллельных блочных методов решения задачи Коши на вычислительном кластере. Разработанная программная система может быть использована для решения задачи Коши многошаговым параллельным блочным методом.Параллельные многошаговые блочные методы численного решения задачи Коши для ОДУ
В данной главе рассматриваются основы распараллеливания многошаговых алгоритмов решения задачи Коши для ОДУ. Выведем формулы и найдем приближенное решение задачи Коши для дифференциального уравнения первого порядка:y'=f(x,y)
(1.1)
y(x0)=y0
(1.2)
- i =0,1,…,k - номер точки для каждого блока;
- tn,i - точка n –го блока с номером i;
- точка tn,0 - начало блока n, а tn,k – конец блока;
- tn,k = tn+1,0 .;
- начальная точка в блок не включается.
Описание параллельных многошаговых блочных методов численного решения задачи Коши для ОДУ
В случае многошагового блочного метода начальный блок будет содержать точки сетки, в которых начальные значения приближенного решения необходимы для продолжения расчетов.Схема разбиения на блоки для m-шагового k-точечного метода представлена на рисунке 1.1.

Рисунок 1.1 – Схема разбиения на блоки для m-шагового k-точечного метода
(Анимация состоит из 4 кадров, 78Кб с задержкой в 1 с между кадрами; задержка до повторного воспроизведения составляет 2с; количество циклов воспроизведения - 7)
В общем случае уравнение многошаговых разностных методов для блока из k точек при использовании вычисленных значений приближенного решения в m предшествующих блоку узлах, с учетом введенных выше об обозначений можно записать в виде:
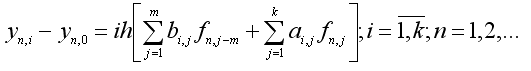
(1.3)
Определить коэффициенты ai,j и bi,j можно аппроксимируя подынтегральную функцию одного переменного f(x,y(x)) алгебраическим интерполяционным многочленом Лагранжа Lk(t), который в узлах xn,j-m принимает значения f(xn,j-m,y(xn,j-m)), j=1,2,...,m+k. Далее необходимо проинтегрировать его в пределах (tn, tn+iτ), i=1,k
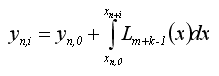
(1.4)
В итоге будут получены искомые формулы.
Для вычисления приближенных значений решения задачи Коши коллокационным многошаговым блочным методом необходимо решить нелинейную систему уравнений (1.3). Можно для этого использовать следующий итерационный процесс:
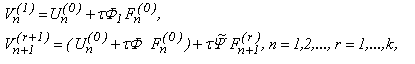
(1.5)
Закрепим каждый процессорный элемент за точкой n-го блока, которая вычисляется. Тогда каждый из k процессоров сначала будет вычислять значения начального вектора по методу Адамса-Башфорта.
Далее каждый процессор будет находить соответствующий вектора со значениями правых частей fn,j=f(tn+jτ,un,j)) . После чего будет осуществляться обмен между процессорными элементами для выполнения дальнейших вычислений и потом по заданным формулам, будут находиться значение вектора приближенного решения. Если количество процессоров будет меньше, чем размерность блока, то некоторые процессорные элементы будут последовательно вычислять значения нескольких точек блока, что в итоге увеличит общее время вычислений.
При решении системы дифференциальных уравнений возможны два варианта распределения процессоров:
- для каждого уравнения выделяется P1=P/k процессоров, где P- общее число процессоров, а k- число уравнений в системе. P1 процессоров участвуют в параллельном вычислении значений блока: m/P1 значений точек блока вычисляются на каждом из процессоров
- для каждого блока выделяется P1=P/m процессоров, где P- общее число процессоров, а m- число точек в блоке. k/P1 уравнений системы вычисляются на каждом из процессоров
- вектор начальных приближений искомой функции Ui,j;
- вектор значений ОДУ для сеточных функций в узлах предыдущего блока Fi,j;
- вектор значений элементов ψ i,j , который является i–ым столбцом матрицы Ψ;
- вектор значений элементов φ i,j , который является i–ым столбцом матрицы Φ;
- вектор значений элементов F i,j , который является i–ой строкой матрицы F.
Погрешность аппроксимации блочных методов
Коэффициенты ai,j и bi,j выбираются таким образом, чтобы разностное уравнение (1.3) аппроксимировало дифференциальное уравнение с достаточно гладкой правой частью с некоторым порядком s. Это означает, что невязка ρ , которая получается после подстановки точного решения y(x) дифференциального уравнения в разностное уравнение (1.3).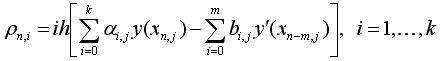
(1.6)
Величина
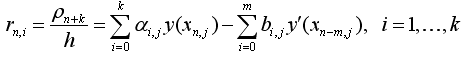
(1.7)
Называется погрешностью аппроксимации дифференциального уравнения разностным уравнением (1.3).
Если воспользоваться формулой Тейлора для y(xn+i) и y'(xn+i) , то погрешность аппроксимации будет иметь вид:
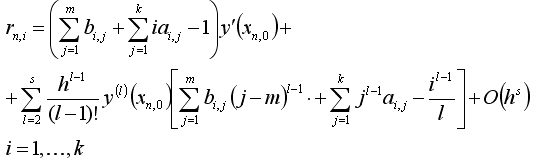
(1.8)
Из (1.8) видно, что для того, чтобы величина rn,i имела порядок O(h5) необходимо выполнение условий
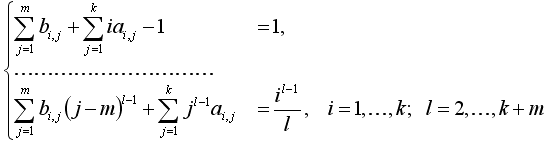
(1.9)
Оценка эффективности параллельных многошаговых блочных методов численного решения задачи Коши для ОДУ
Критериями оценки параллельных алгоритмов, как правило, выступают две величины:- ускорение Sp
- эффективность Ep
- T1- время выполнения последовательного алгоритма;
- Tp – время выполнения параллельного алгоритма, распараллеленного на k процессоров;
- Tf – время вычисления значения функции f(t,x);
- Tсл – время выполнения операции сложения;
- Tум – время выполнения операции умножения;
- Tоб – время передачи числа соседнему процессору.
Sp(n)=T1(n)/Tp(n)
(1.10)
Эффективность (efficiency) использования параллельным алгоритмом процессоров при решении задачи определяется соотношением
Ep(n)=T1(n)/(pTp(n))=Sp(n)/p
(1.11)
Для оценки ускорения m-шагового k-точечного блочного метода сравним время его выполнения на мультипроцессорной системе со временем выполнения алгоритма m-шагового метода Адамса-Башфорта на однопроцессорной ЭВМ. Метод Адамса-Башфорта можно рассматривать как многошаговый одноточечный блочный метод. Последовательное k-кратное применение формул Адамса-Башфорта позволяет вычислить приближенное решение в тех же k узлах блока, в которых параллельно за k итераций может быть вычислено решение m-шаговым k-точечным блочным методом. В этом случае время вычисления будет приблизительно одинаково. Точность приближенного решения, полученного m-шаговым k-точечным блочным методом, имеет порядок O(τm+k), а точность приближенного решения, полученного по m шаговой формуле Адамса-Башфорта, имеет порядок O(τm+1).
Для того, чтобы получить решения с одинаковой точностью для метода Адамса-Башфорта необходимо, чтобы шаги сетки для метода Адамса-Башфорта и m-шагового k-точечного блочного метода удовлетворяли условию
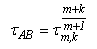
Например: для решения задачи 4-шаговым 4-точечным блочным методом выбран шаг τm,k =0.01, то для обеспечения той же точности решения методом Адамса-Башфорта необходимо взять шаг τA,B =0.0063.
Время выполнения последовательного алгоритма во всех k узлах:
T1=k2*tf+(k+1)*(tум.+tсл.)
(1.12)
Время параллельного вычисления приближенных значений решения на линейке из процессоров:
Tk=(k+1)*tf+(3k2+2k+1)*tсл.+(3k2+3k+1)*tум.+k(2k+1)об.
(1.13)
Следует отметить, что на динамические характеристики параллелизма влияют латентность и время передачи одного слова. Полученная зависимость коєффициента эффективности от латентности является обратнопропорциональной (при уменьшении величины латентности увеличивается эффективнность алгоритма решения задачи) и приведена на рисунке 1.2.
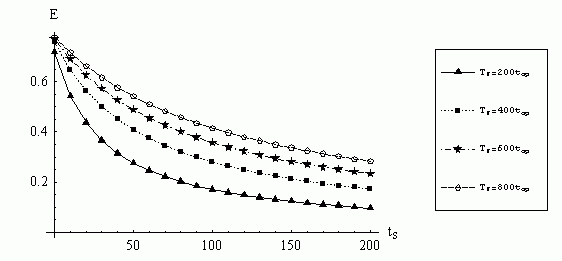
Рисунок 1.2 – Зависимость коэффициентов эффективности параллельного многошагового блочного метода от величины латентности, ts
С ростом величины латентности время, затрачиваемое на обмен данными между процессами увеличивается, а эффективность параллельных вычислений уменьшается. При расчете ускорения и эффективности многошагового блочного метода наибольшее влияние на показатели оказывает время вычислений правой части уравнений, т.к. времена выполнения арифметических операций и обмена значительно меньше времени вычисления правой части. Зависимость коэффициентов ускорения и эффективности от времени вычисления правой части уравнения Tf и числа точек блока k приведены на рисунках 1.3, 1.4 .
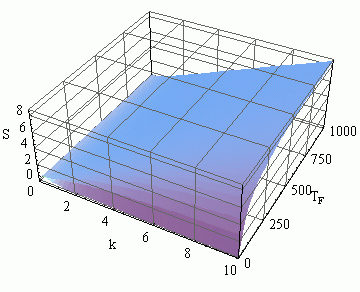
Рисунок 1.3 – Зависимость коэффициента ускорения параллельного многошагового блочного метода от времени вычисления правой части, Tf и числа точек блока k
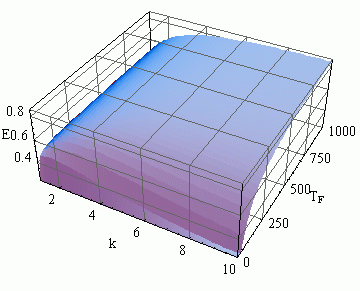
Рисунок 1.4 – Зависимость коэффициента эффективности параллельного многошагового блочного метода от времени вычисления правой части, Tf и числа точек блока k
Ускорение k-точечного многошагового параллельного алгоритма можно считать приближенно равным
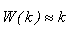
и эффективность будет равна
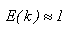
При этом характеристики параллелизма в системах с кольцевой структурой оказываются хуже, чем в системах с топологией гиперкуб и тор, что свидетельствует про сильное влияние время обмена данными между процессорами в параллельных вычислительных системах. Между временем вычисления правой части и эффективностью существует прямая зависимость: при увеличении трудоемкости вычислений правых частей, эффективность рассмотренных методов увеличивается. Также следует отметить, что в связи с тем, что число точек блока связано с числом используемых процессоров, при увеличении числа точек в блоке возростает коэффициент ускорения S и уменьшается коэффициент эффективности E [4].
Выводы
В данном разделе были рассмотрены многошаговые блочные методы решения задачи Коши для обыкновенных дифференциальных уравнений, показана погрешность аппроксимации данных методов, приведены оценки эффективности данных методов.В дальнейшем при выполнении магистерской диссертации будет разработана программная система для решения задачи Коши многошаговым параллельным блочным методом. Использование разрабатываемой программной системы позволит оценить показатели эффективности и точность параллельного решения задачи Коши исследуемым методом.
Список использованной литературы
- Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. - Н.Новгород, ННГУ, 2001
- Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990. – 512с.
- Фельдман Л.П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами // Научные труды ДонНТУ. Серия: Информатика, моделирование и вычислительные методы, (ИКВТ-2000), выпуск 15: Донецк: ДонНТУ, 2000, с. 34-39.
- Дмитриева О.А. Модели отображения многошаговых алгоритмов на параллельные вычислительные системы с топологией гиперкуб//Науковi працi Донецького державного технiчного унiверситету. Серiя: Проблеми моделювання та автоматизації проектування динамічних систем, випуск 46: – Донецк:, 2002. с. 154-161.
- Фельдман Л.П., Дмитриева О.А. Разработка и обоснование параллельных блочных методов решения обыкновенных дифференциальных уравнений на SIMD-структурах. //Научн. тр. Донецкого государственного технического университета. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 29. – Севастополь: «Вебер», 2001. – с. 70-79.
- Kazufumi OZAWA, Susumu YAMADA “Parallel block methods for solving nonstiff equations with stepsize control“,Graduate school of information science, Tohoku University, 2006
- Воеводин В.В., "Вычислительная математика и структура алгоритмов.".-М.: Изд-во МГУ, 2006.-112 с.
- van der Houwen P.J., “Parallel Step-by-Step Methods”, CWI Amsterdam, 1991
- Самарский А.А., Гулин А.В. Численные методы.- М.: Гл. ред. физ.-мат. лит., 1989.– 432 с.
- Воеводин В.В. Математические основы параллельных вычислений. - М.: Изд-во МГУ, 1991. - 345 с.
http://window.edu.ru/window_catalog/pdf2txt?p_id=6579
http://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/60205/1/0944-2.pdf
http://www.parallel.ru/info/parallel/voevodin/
http://ftp.cwi.nl/CWIreports/1991/NM-R9116.pdf