Traditional surface texture analysis involves filtering surface profiles into different wavelength bands commonly referred to as roughness, waviness and form. The primary motivation in filtering surface profiles is to map each band to the manufacturing process that generated the part and the intended functional performance of the component. Current trends in manufacturing are towards tighter tolerances and higher performance standards that require close monitoring of the process. Thus, there is a need for finer bandwidths for process mapping and functional correlation. Wavelets are becoming increasingly popular tools for filtering profiles in an efficient manner into multiple bands. While they have broadly been demonstrated as having superior performance and capabilities than traditional filtering, fundamental issues such as choice of wavelet bases have remained unad-dressed. The major contribution of this paper is to present the differences between wavelets in terms of the transmission characteristics of the associated filter banks, which is essential for surface analysis. This paper also reviews fundamental mathematics of wavelet theory necessary for applying wavelets to surface texture analysis. Wavelets from two basic categories — orthogonal wavelet bases and biorthogonal wavelet bases are studied. The filter banks corresponding to the wavelets are compared and multiresolution analysis on surface profiles is performed to highlight the applicability of this technique.
       Atypical engineering surface consists of a range of spatial fre-quencies. The high frequency or short wavelength components are referred to as roughness, the medium frequencies as waviness and low frequency components as form. Historically, it has been accepted that different aspects of the manufacturing process generate different wavelength regimes and these affect the function of the part differently. By separating surface profile into various bands, it is possible to map the frequency spectrum of each band to the manufacturing process that generated it or to the specific functional aspects of the part. Thus, filtering of surface profiles serves as a useful tool for process control and functional correlation. Recent advances in filtering of surface profiles are reviewed by Raja . A major issue with current approach to filtering and parameterization is the lumping of a large bandwidth into a single entity such as roughness, waviness or form. The current state of art in filtering of surface texture is limited to obtaining parameters that are averaged over a large wavelength regime, such as roughness. The Gaussian filter probably the most widely used filter in surface metrology today, is incapable of separating a profile into fine bandwidths because of its transmission characteristics. As current manufacturing trends are towards higher performance, increased warranty periods and tighter tolerances, there is a need for close monitoring of the process. Thus, filtering of profiles to obtain finer bandwidths that better reflect the variations in the process or the intended function of the component is required. One recent development in this regard is the use of wavelets for surface texture analysis. The wavelet is an attractive tool in surface texture analysis because it can decompose a surface (2D profile or 3D surface) into multi-scale representation in a very efficient way. While wavelets have broadly been demonstrated as having superior performance and capabilities than traditional filtering, fundamental issues such as choice of wavelet bases have remained un-addressed. The major contribution of this paper is to present the differences between wavelets in terms of transmission characteristics of their associated filter banks, which is essential for surface analysis.

      It is well known from Fourier theory that a signal can be represented as the sum of a series of sines and cosines. However, the sines and cosines that comprise the bases of Fourier analysis are nonlocal functions that have only frequency resolution and no time resolution. This means that although Fourier transform might be able to determine all the frequencies present in a signal, it is unable to show when or where they are present. The Heisenberg uncertainty principle states that multiplication of the temporal variance and the frequency variance of a basis function with unit norm will always be greater than half. Therefore, a tradeoff exists between temporal (spatial in surface analysis) localization and frequency localization of a basis. Localization implies a basis function has non-zero value in a finite domain. For instance, a sinusoidal signal has infinite support (no localization) in time domain and zero-length support (one definite frequency) in frequency domain. In contrast, an impulse signal has zero-length support (one definite time) in time domain and infinite support (no localization) in frequency domain. Wavelets overcome the shortcoming of sinusoids and impulses by having localization in both time (spatial) and frequency domain to obtain resolution in both domains.

      In wavelet analysis, a signal is transformed to a series using a family of wavelet bases. Largescale bases represent low frequency components and small-scale bases represent high frequency com-ponents. The end result is a collection of time-frequency represen-tations of the signal with different resolutions, and is commonly referred to as the multiresolution representation. Multiresolution analysis was made practical by the discoveries of Mallat and Meyer who showed the equivalence between pyramid algorithm used in discrete two-channel filter banks and dyadic wavelet transform (discrete wavelet transform with dyadic-scaling). Whilethe pyramid algorithm enables fast implementation of multireso-lution analysis, the wavelet theory provides strong mathematical ground for it.

      This section briefly addresses the necessary mathematics for wavelet analysis. Mallat and Strang provide a comprehensive review of wavelet theory and filter banks. A condensed summary is presented here as an introduction to readers unfamiliar with the subject. The goal of wavelet analysis is to decompose a given signal over a family of wavelets, which is generated from a mother wavelet by dilation and translation. A mother wavelet is a square-integrable function ψ(x) with a zero average, e.g.

(1)

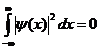(2)

      A family of wavelets is obtained by scaling ψ(x) by S and translating it by t, the factor s^1/2 is for energy normalization across different scales:

(3)

      The wavelet transform of function f(x) at position t and scale s is

(4)

      with

(5)

      The Fourier transform of

(6)

      Because

      the wavelet works as a band-pass filter. The scale s reflects the tradeoff between spatial resolution and frequency resolution. As the scale increases, the spatial resolution decreases and frequency resolution increases in accordance with Heisenberg’s uncertainty principle. The signal can be reconstructed by inverse wavelet transform as follows:

(7)

      where C_ψ is calculated by

(8)

      While Wf(t,s) is usually only calculated at small scales s<s₀ as high frequency details, to reconstruct f(x) a complement of information at large scales s>s₀ is necessary as low frequency approximation. This is obtained by introducing a scaling function ф that is an aggregation of wavelets at scales larger than s₀=1. The modulus of its Fourier transform is defined by

(9)

      From eq. (9)

(10)

      So the scaling function can be interpreted as the impulse response of a low-pass filter. Denoting

      and

      Then the low frequency approximation of f at the scale s is

(11)

      Therefore eq. (7) can be rewritten as

(12)

      The function can be transformed as the sum of the approximation at a certain scale and the details at smaller scales. The transform described above is the continuous wavelet transform (CWT), which serves as mathematical basis for all practical wavelet applications. Details of CWT are explained in Daubechies and Mallat.