Параллельный алгоритм построения дискретной марковской модели неоднородного кластера

Автор: Кучереносова О.В.

Источник: Наукові праці Донецького національного технічного університету. – Донецьк, ДонНТУ, 2010.

Общая постановка проблемы

В настоящее время существует большое количество задач, требующих применения мощных вычислительных систем, среди которых задачи моделирования работы систем массового обслуживания и управления, распределённых систем, сложные вычислительные задачи и др. Для решения таких задач всё шире используются кластеры, которые становятся общедоступными и относительно недорогими аппаратными платформами для высокопроизводительных вычислений. Кластер представляет собой множество компьютеров (узлов), соединенных между собой высокоскоростными каналами связи, а специальное программное обеспечение позволяет организовать параллельную работу узлов.

Однако эффективность применения кластерных систем в настоящее время наталкивается на целый ряд нерешённых проблем, касающихся как их программного обеспечения (языков, технологий и инструментальных сред параллельного программирования), так и собственно организации параллельных вычислений и эффективности их выполнения. Объединение большого количества компьютеров в единый вычислительный комплекс породило такие задачи, как сбалансированность нагрузки, выявление узких мест в вычислительной системе, обеспечение заданного времени ответа при работе большого количества пользователей, выбор оборудования при максимальной производительности при ограниченной заданной стоимости и т.д.

В связи с большим количеством создаваемых параллельных вычислительных систем и, во многих случаях, неэффективным их использованием, работы в этом направлении требуют дальнейшего развития и не утрачивают своей актуальности.

Постановка задач исследования

В настоящее время значительный вклад в решение проблем создания новых многопроцессорных архитектурных реализаций и оценки их эффективности. Вносят дискретные марковские модели, которые по сравнению с непрерывными более точно отражают работу вычислительных систем. Подобные задачи обладают большой размерностью и не могут быть эффективно реализованы на однопроцессорных ЭВМ. Решением этой проблемы является распараллеливание алгоритма построения дискретных марковских моделей на несколько вычислительных модулей.

Решение задачи и результаты исследований

В модели с разделяемыми дисками каждый узел в кластере имеет свою собственную память, все узлы совместно используют дисковую подсистему [2]. Такие узлы связаны высокоскоростным соединением для того, чтобы передавать регулярные контрольные сообщения. При отсутствии таких сообщений определяются неисправности в вычислительной системе. Узлы в кластере обращаются к дисковой подсистеме по системной шине.

Одна из разновидностей кластера с совместным использованием дискового пространства представлена его упрощенной моделью на рис. 1.

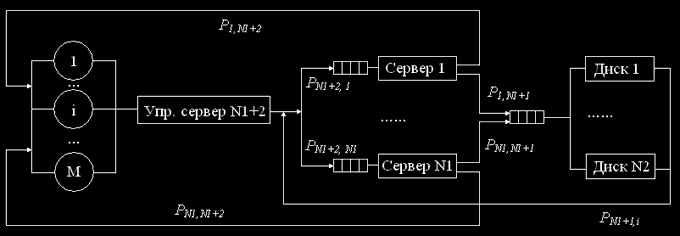
Рис.1. Структурная схема марковской модели неоднородного кластера с совместным использованием дискового пространства

Входной узел (управляющий сервер) распределяет между серверами приложений (выполняющими неодинаковые приложения) задачи. Количество серверов – приложений – N1. Каждый из них может обратиться к данным, расположенным на дисках, количество которых N2. Ввиду ограниченных вычислительных возможностей будем считать, что количество задач, обрабатываемое такой вычислительной системой не более М.

Построим дискретную марковскую модель. Так как дисковые накопители однородны, представим их многоканальным устройством.

Требования, поступающие на обслуживание на каждый из серверов, поступают в соответствующую ограниченную очередь (не более М), из которой на обслуживание выбираются по правилу «первый пришел – первый обслужился»[1].

Задачи, обрабатываемые на таком кластере, неоднородные имеют следующие характеристики:

• P_N1+2,i – вероятность запроса к i-му серверу, i=1..N1,
• P_i,N1+1 – вероятность запроса i-го сервера к одному из N2 дисков, i=1..N1,
• P_{i, N1+2} – вероятность завершения обслуживания задачи i-м сервером, i=1..N1,
• P_N1+1,i – вероятность завершения обслуживания задачи одним из N2 дисков и поступление на i-й сервер, i=1..N1,
• P_N1+2,0 – вероятность завершения обслуживания задачи,
• P_0,N1+2 – вероятность появления новой задачи.

Для вычислительных ресурсов примем, что длительности времен обслуживания заявок на входном узле, сервере приложений или дисковом массиве, соответственно, имеют геометрическое распределение со средним, равным T_i, (i=1..N1+2). Тогда

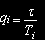– вероятность завершения обслуживания задачи на входном узле, сервере приложений или дисковом массиве, соответственно, (i=1..N1+2),

r_i – вероятность продолжения обслуживания задачи на входном узле, сервере приложений или дисковом массиве, соответственно, (i=1..N1+2), r_i=1-q_i.

За состояние системы примем размещение М заявок по N узлам 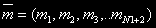, где m_i – количество задач в i-ом узле. Необходимо определить все возможные состояния. Обозначим множество состояний через 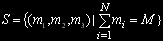. Число состояний системы для одного и того же количества задач j= 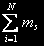равно числу размещений j задач по N узлам и определяется по формуле 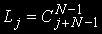, общее количество состояний вычисляется так:

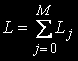
Вектор 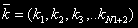определяет количество устройств в каждом узле ВС.

Матрица переходных вероятностей P={P_ij} имеет размерность LxL. Для ее построения используются:

• вектор определяющий число загруженных устройств в s-ом узле обработки программ;
• вектор , каждая компонента которого представляет изменение числа задач в s-ом узле;
• множество J номеров узлов обработки, в которых < 0;
• , отражающая разность количества обрабатываемых задач в состоянии и состоянии ;
• N-мерный вектор , индикатор распределения задач, обслуженных серверным узлом по остальным узлам системы;
• N-мерный вектор 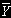, индикатор распределения задач, обслуженных узлами системы;
• вектор ,определяющий распределение по каналам минимального числа (i=1..N) программ, обслуженных процессорным узлом;
• вектор , в котором компонента _i (i=1..N), равна максимально возможному числу программ, которые дополнительно, сверх могут быть обслужены серверным узлом, а _s, аналогично, равна максимально возможному числу программ, которые дополнительно сверх обязательно поступивших в s-й узел обработки, могут еще поступить в него.

Для определения вектора стационарных вероятностей состояний 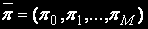необходимо решить систему линейных алгебраических уравнений (СЛАУ),

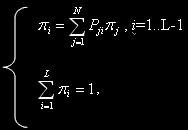
соответствующую рассмотренной модели кластера, где
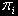– вероятность застать систему в i-м состоянии.

Стационарные вероятности дают возможность определить средние значения временных характеристик обслуживания и занятости устройств вычислительной системы, а именно: среднее число занятых устройств в s-м узле, загрузка устройств, среднее число задач в s-м узле, среднее числo задач, находящихся в очереди к s-му узлу, среднее время пребывания в s-м узле, среднее время ожидания в s-м узле, среднее время пребывания в вычислительной системе, среднее время ожидания в вычислительной системе.

Распараллелим алгоритм построения дискретной марковской модели.

Алгоритм состоит условно из двух частей: вычислений матрицы переходных вероятностей и вектора стационарных вероятностей.

Вычисление элемента матрицы переходных вероятностей не зависит от соседних элементов, следовательно, в основе параллельной реализации этой части параллельного алгоритма можно использовать принцип распараллеливания по данным [3].

В качестве базовой подзадачи можно взять расчет строки, столбца или блока матрицы переходных вероятностей. Это позволит сбалансировать загрузку вычислительных модулей кластера. Каждый процесс определяет, какие строки (столбцы, блоки) матрицы переходных вероятностей он должен вычислить и отправить управляющему процессу. Схема параллельного алгоритма приведена на рисунке 2.

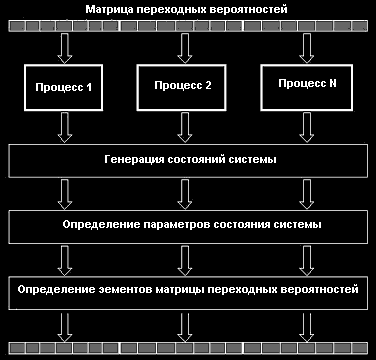
Рис.2. Параллельный алгоритм построения матрицы переходных вероятностей

Расчет стационарных вероятностей можно реализовать с использованием итерационного алгоритма, в котором в качестве базового используется алгоритм умножения матрицы на вектор. Схема алгоритма расчета вектора стационарных вероятностей представлена на рис.3. Для распараллеливания задачи умножения матриц можно использовать ленточную (по строкам, по столбцам) или блочную схему разделения данных.

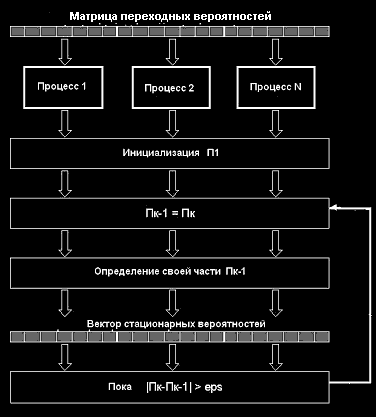
Рис.3. Параллельный алгоритм расчета вектора стационарных вероятностей

Выводы

В работе предложен параллельный алгоритм построения дискретной марковской модели неоднородного кластера, который дает возможность оценить эффективность работы неоднородной параллельной вычислительной системы с совместным использованием дискового пространства.

Результаты моделирования могут быть использованы для повышения эффективности работы, для синтеза, анализа, реконфигурации кластерных систем подобного типа.

В дальнейшем этот алгоритм можно исследовать на параллельных структурах различной топологии.

Список литературы

1. Михайлова Т.В. Повышение эффективности кластерных вычислительных систем на основе аналитических моделей. // Автореферат диссертации на соискание ученой степени к.т.н. — Донецк, 2007. — 20 с.
2. Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя.— К.:«ДиаСофт», 1998. — 432 с.
3. Фельдман Л.П., Михайлова Т.В., Ролдугин А.В. Реализация параллельного алгоритма построения марковских моделей. // Наукові праці ДонНТУ. Серія: Інформатика, кібернетика та обчислювальна техніка, випуск 10. — http://www.nbuv.gov.ua/portal/natural/Npdntu/ikot/2009_10/09flppmm.pdf

© Магистр ДонНТУ, Кучереносова Ольга Владимировна, 2010