Решение задач теории игр графическим методом
Евтюшкина А.Б.
Руководитель Дацун Н.Н.
Источник: Матеріали VIII міжвузівської студентскої наукової конференції «Студентська молодь та наука: цінності, досягнення, перспективи», 19 травня 2006 р., Том 1. – Донецьк, ДІПП, 2006. – 96 c., с.34-36.
Задачами о принятии решений в условиях неопределенности занимается теория игр статических решений.
К задачам теории игр относятся задачи, связанные с конфликтными ситуациями, в которых сталкиваются две (или более) враждующие стороны, преследующие различные цели, причем результат любого мероприятия каждой из сторон зависти от того, какой образ действия (стратегию) выберет противник.
В парной игре у каждого противника есть определенный набор стратегий. Назовем их условно для первого игрока: А1, А2,…Аm; для второго игрока: В1, В2,…Вn (m, n количество стратегий игроков – игра m × n).
В результате выбора игроками любой пары стратегий А(i) и B(j) однозначно определяется исход игры – выигрыш a(i,j) игрока А (положительный или отрицательный) и проигрыш -a(i,j) игрока В. Значения a(i,j) известны для любой пары стратегий А(i), B(j). На основе этих данных можно построить платежную матрицу (матрицу игры), элементами которой являются выигрыши. Строки таблицы соответствуют стратегиям игрока A, столбцы – стратегиям игрока В.
| B1 | B2 | ... | Bn | |
| A1 | a11 | a12 | ... | a1n |
| A2 | a21 | a22 | ... | a2n |
| ... | ... | ... | ... | ... |
| Am | am1 | am2 | ... | amn |
Стратегия или совокупность стратегий, которые принесут игроку максимальный выигрыш (минимальный проигрыш), называется оптимальной стратегией.
Цель теории игр – определение оптимальной стратегии каждого игрока.
Если у каждого игрока оптимальная стратегия единственная, то она называется чистой, и это свидетельствует о наличии в игре седловой точки. Такие игры решаются методом «минимакса».
Смешанная оптимальная стратегия состоит в том, что игроку нужно применить не одну какую-то стратегию, а несколько перемежая их случайным образом.
Существует несколько методов для решения игры в смешанных стратегиях, один из них – графический метод. Этот метод позволяет определить смешанные оптимальные стратегии для каждого игрока, если один из них имеет ровно две стратегии:
SA = (p1,p2), SB = (q1,q2),
где р1, р2, q1, q2 – вероятность применения стратегий.
Исходными данными являются количество стратегий игроков (не менее двух стратегий), их названия, а также сама платежная матрица (m × n).
Для автоматизации построения модели конфликтной ситуации и ее решения необходимо разработать компьютерную программу.
При вводе данных в Visual Basic для названия стратегий можно использовать список, для ввода платежной матрицы используется набор текстовых окон, расположенных на форме в виде двумерной матрицы, с метками, обозначающими стратегии игроков во главе строк и столбцов матрицы. После ввода текстовые окна числовые значения переписываются в двумерный массив А(0..10,0..10). А затем для упрощения построения графика делаем массив положительно определенным: находим минимальный элемент массива и записываем его в переменную, например, min, а затем все элементы массива увеличиваем на абсолютное значение min.
Для начала нужно выбрать пару активных стратегий игроков, которые войдут в оптимальную стратегию. Платежную матрицу нужно упростить до матрицы (2 × n) или (m × 2), для этого ищем заведомо невыгодные стратегии. Для игрока А, если все элементы одной стратегии почленно меньше или равны элементам какой-нибудь другой стратегии (так как игрок А максимизирует выигрыш), то такая стратегия заведомо невыгодна и ее нужно удалить. Для игрока В все элементы заведомо невыгодной стратегии больше или равны элементам другой стратегии (так как игрок В минимизирует проигрыш). Поиск таких стратегий можно организовать программным путем, сравнивая поэлементно все значения строк и столбцов двумерного массива А(10,10). Найденная невыгодная стратегия удаляется из массива. Если матрица не сократилась до нужных размеров, программа предлагает пользователю самому удалить стратегию, нажав на ее метке слева или сверху.
Визуально на форме это можно изобразить таким образом: Строка или столбец текстовых окон зачеркивается линией. Учитывая Z-порядок уровней размещения объектов на форме, линии можно заменить рамками или командными кнопками с измененными размерами (при загрузке формы эти элементы управления делают невидимыми).
Так как в Visual Basic нельзя создать двумерный массив элементов управления, то для соответствия номера строки (столбца) в матрице А(10,10) и на форме в последние колонки матрицы нужно записать номер этой строки (столбца). При сравнении элементов последние колонки не участвуют, а при удалении записей из матрицы сдвигаются вместе со всеми элементами. По этим колонкам определяется номер проявляющейся рамки зачеркивания.
Перед тем как удалять из матрицы стратегии, а также после каждого вычеркивания пользователем, нужно проверить матрицу на наличие седловой точки, так как она свидетельствует о решении игры в чистых стратегиях и данным методом не рассматривается. Если седловая точка есть, то программа предлагает пользователю вернуться к вводу данных.
Теперь переходим к построению графика. Его удобнее всего рисовать в элементе управления PictureBox.
Делаем разметку листа. Вдоль оси У рисуем первую стратегию игрока А, параллельно ей через точку (1;0) – вторую. (рис. 1)
Пусть игрок А применяет стратегии А1, А2, а противник – стратегию В1; она дает на оси I-I точку с координатой у = a(0,1). а на оси II–II – точку с координатой у = a(1,1). Проводим через эти точки прямую B1-B1. По аналогии строим остальные «линии-стратегии»:
Нам нужно далее найти оптимальную стратегию SA (такую, при которой наш минимальный выигрыш обращался бы в максимум). Для этого строим нижнюю границу выигрыша при стратегиях В1, В2,…Вn. Это ломаная линия, образованная самыми нижними отрезками «линий-стратегий» (жирная пунктирная линия). Выбираем на линии нижней границы выигрыша наивысшую точку, в которой выигрыш достигает максимума. На рисунке 1 максимум достигается в точке N. Стратегии, линии которых пересекаются в этой точке, являются активными стратегиями противника.
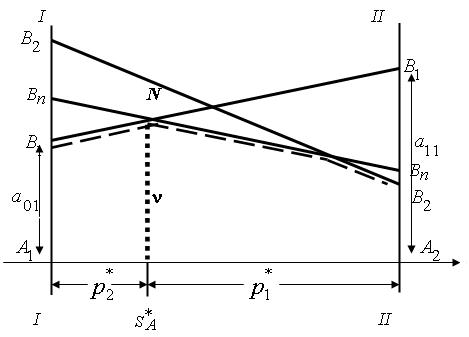
Точка N определяет решение и цену игры: ордината точки N есть цена игры v, ее абсцисса равна р2*, а расстояние до правого конца единичного отрезка равно р1*. Итак, получена оптимальная смешанная стратегия нашего игрока SA* = ( p1*, p2*) и цена игры v , которую нужно скорректировать в связи с положительным определением матрицы игры v = v + min.
Для нахождения нижней границы игры нужно уравнения прямых в отрезках перевести в уравнения прямых в каноническом виде.
а1 = у2 – у1
в1 = х1 – х2
с1 = а1×х1 – в1×у1
Так как х1 = 0, а х2 = 1, то уравнение принимает вид:
у = ( у2 – у1)×х+ у1
Затем нужно найти крайние левые и правые точки:
Левая х = 0, у – min в строке a(0,i)
Правая х = 1, у – min в строке a(1,i)
Далее находим точки пересечения прямых по формулам:
х = (b2 – b1)/(к1 – к2)
у = к1×х+b1
Для первой прямой (В1) ищем самую левую точку пересечения с другой прямой (но правее предыдущей исходной точки). Линию (х1, у1) – (х2, у2) выделяем другим цветом (х1,у1 – точка начала, х2,у2 – точка конца). То же проделываем с прямой, с которой пересеклась первая прямая (если через одну точку проходит больше двух прямых, выбираем ту прямую, у которой при х = 1, у → min). Если точка пересечения не нашлась, рисуем последнюю линию (х1,у1) – (1,у). Параллельно ищем точку пересечения с максимальным у, ордината которой – цена игры, а абсцисса – величина р2.
Аналогично для стратегий игрока В. Только ищем верхнюю границу выигрыша. (рис. 2)
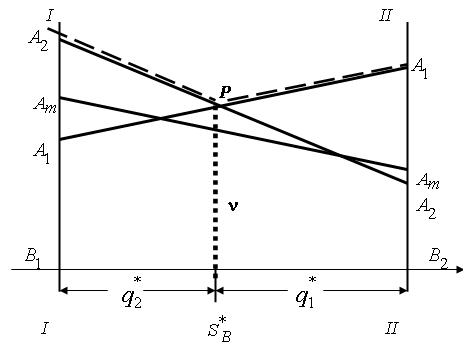
Лицо, принимающее решение, получает результат решения не только в графическом виде, но и в виде рекомендации. Она содержит процентное соотношение использования каждой активной чистой стратегии в смешанной для каждого игрока, а также цену игры (выигрыш/проигрыш) каждого из игроков.
Литература
- Вентцель Е.С. Исследование операций. – М.: Наука, 1972 г., – 552 c.