ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

В настоящее время развитие робототехники находится на высоком уровне. Роботы используются в промышленной индустрии, полностью или частично они заменяют собой человека, осуществляют технические операции различной сложности. Они также широко используются в повседневной жизни, помогая людям. То есть роботы все больше взаимодействуют с людьми. Взаимодействие между человеком и роботом со сложной кинематикой зависит от системы управления роботом. Чтобы создать эту систему, компьютерных и технических знаний недостаточно. Вследствие этого, многие исследователи обращаются к фундаментальным биологическим знаниям.

Одно из свойств биомеханических систем – это податливость под воздействием внешних сил. В этом проекте исследуется система управления податливостью робота-манипулятора Катана. В основании звеньев робота находится система двигатель-редуктор типа Harmonic Drive. Наличие этой системы вызывает появление упругостей в звеньях робота. Широко распространено управление системой Гармоник Драйв с помощью ПИД-регулятора (англ. PID).

1. Актуальность темы

Новизна работы состоит в совершенствовании системы управления податливостью электромеханических роботов за счет применения биологически подобных контроллеров (нелинейных осцилляторов), что позволяет повысить адаптивность системы по отношению к вариации ее параметров и условий работы, что особенно важно для случая взаимодействии робота с человеком. Оценивается надежность робототехнической системы, предлагается улучшение этой системы.

2. Цель и задачи исследования, планируемые результаты

Целью данной работы является усовершенствование системы управления податливостью электромеханических роботов со сложной кинематикой при физическом взаимодействии с человеком и оценка ее надежности.

Основные задачи исследования:

  1. Принципы управления податливостью.
  2. Применение волновых редукторов в робототехнике.
  3. Математическая модель робота с учетом упругостей передач и кинематики звеньев робота.
  4. Математическое моделирование биологически подобных нейронных осцилляторов.
  5. Оценка надежности системы управления робота Катана.
  6. Экспериментальные исследования с роботом.

3. Обзор исследований и разработок

3.1 Обзор международных источников

В звеньях робота Катана установлены двигатели постоянного тока и редукторы типа Harmonic Drive. Редуктор Harmonic Drive состоит из трех частей: волновой генератор, гибкая часть с внешними зубцами и круговая часть с внутренними зубцами [1].

Компоненты редуктора Harmonic Drive. Картинка взята из источника 1

Рисунок 1 – Компоненты редуктора Harmonic Drive

Преимущества редуктора: большой крутящий момент, концентрическая конструкция, легкость, компактность, отсутствие зазора, высокая эффективность, обратная управляемость.

Благодаря своим преимуществам редукторы Гармоник Драйв очень популярны в промышленных манипуляторах. Но они имеют и недостатки: высокая упругость, резонансные вибрации, трение [1]. В манипуляторах с непосредственным приводом выходной вал двигателя соединяется непосредственно с выходом звена, и таким образом, сводятся к минимуму нежелательные эффекты передачи, например, зазор, который сложно смоделировать. Также при прямом приводе манипулятора является возможным довольно хороший контроль момента звена [2].

Необходимо отметить, что трение в редукторе является сложным для компьютерного моделирования.

Еще одним недостатком редуктора Гармоник Драйв является то, что динамическое поведение передачи осложняется при желании управлять механическим импедансом [2].

Существует несколько проблем при управлении податливостью робота.

В последние 15 лет большое количество исследований было сосредоточено на управлении упругостью звеньев робота. Начиная с методов управления, разработанных для жестких частей манипулятора, есть некоторые мощные теоретические результаты, касающиеся управления манипуляторами с упругостями в звеньях. К ним относятся сингулярные возмущения (англ. singular perturbation) и интегральное многообразие (англ. integral manifold), линеаризация с обратной связью (англ. feedback linearization), динамическая линеаризация с обратной связью (dynamic feedback linearization), а также адаптивные методы управления [3].

На самом деле, упругость в механических передачах вызывает ошибки в положении робота по причине деформации под действием силы тяжести. Кроме того, она может стать источником нестабильности в случае взаимодействия между роботом и окружающей средой, или когда обратная связь базируется на измерении только переменных составляющих звена (De Luca & Tomei, 1996) [4].

Предполагается, что упругость сосредоточена в "n" звеньях робота и количество переменных конфигурации Лагранжа в динамике робота является удвоенным по сравнению с жестким роботом, что привело к большому количеству "n" двигателей и "n" звеньев в нелинейных уравнениях второго порядка [4].

Контроль импеданса, как один из частных подходов к проблеме управления податливостью движения, очевидно, может быть рассмотрен как один из основных методов современного управления роботом. Фундаментальной целью контроля импеданса в самом общем смысле является получение желаемого динамического соотношения между внешними силами и движениями робота. Тем временем, в многочисленных робототехнических приложениях это динамическое поведение определяется с точки зрения жесткости и матриц затухания по отношению к некоторым декартовым координатам [5].

Пропорциональный, интегральный и дифференциальный (ПИД) алгоритм остается наиболее популярным подходом в управлении промышленными процессами на протяжении развития теории управления. Это объясняется не только простой структурой, которая является простой для понимания, позволяет настройку вручную, но также при использовании алгоритма дает соответствующие результаты в большом количестве различных областей. Тем не менее, оптимальное определение коэффициентов является сложным, и как следствие, многочисленные концепции управления ПИД-регулированием нашли свое отражение в литературе (Astrom & Hagglund, 1984; Zhuang & Atherton, 1993; Daley & Liu, 1998; Liu, Dixon & Daley, 1998; McCormack & Godfrey, 1998) [6].

Большинство правил ПИД-регулирования были разработаны в последние 50 лет. Это, например, правило Ziegler & Nichols (Ziegler & Nichols, 1942), оптимальное правило симметрии (Kessler, 1958; Voda & Landou, 1995), дополнительное правило Ziegler & Nichols (Mantz & Tacconi, 1989), правило некоторого превышения (Seborg, Edgar) [6].

Традиционно, концепция управления роботом-манипулятором может осуществляться простой настройкой ПД или ПИД регулятора на уровне каждого двигателя в звеньях манипулятора. По сути, ПД контроллер является положением и скоростью обратной связи, которая образована замкнутым контуром с хорошими свойствами, когда она применяется к системе с двойным интегратором [7].

Статья [8] демонстрирует возможность компьютерного моделирования нелинейной мускульной системы. Используется ПИД-регулятор и двигатель постоянного тока. Двигатель и ПИД-регулятор соединены в замкнутый контур. Можно изменять параметры ПИД – Kc, Ti, Td. Многослойный персептрон (искусственная нейронная сеть) используется для регулирования параметров ПИД. Показано, что на выходе звена получено поведение, эквивалентное поведению мускула человека.

В магистерской работе с целью контроля упругих звеньев робота используется модель биологического нейрона Ровата-Сельверстона. Американские ученые Роват и Сильверстон в 1997 г. представили аппроксимирующую модель нейрона, для которого определены две группы токов: «быстрый» и «медленный». Токи определяются дифференциальными уравнениями первого порядка. Быстрый ток уравнением (1), а медленный – уравнением (2) [9]:

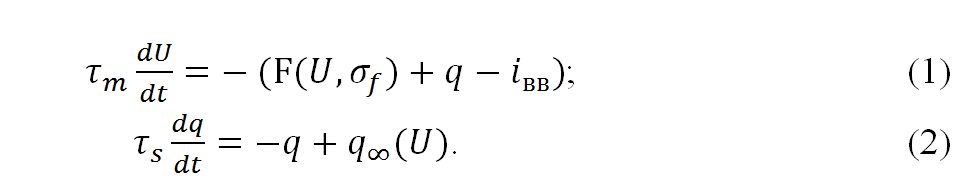
где τm < τs, τm – постоянная времени нейронной мембраны; τs – постоянная времени медленной активации токов; iвв – введенный ток; U – напряжение мембраны; q – медленный ток; U и q – переменные величины;
F(U,σf) – нелинейная вольт-амперная характеристика для быстрого тока, которая определяется выражением:

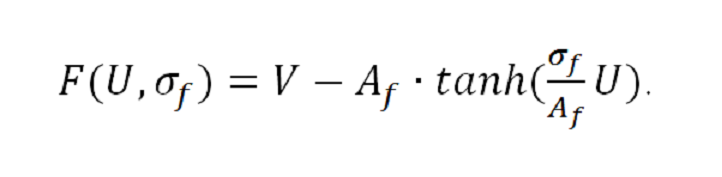
Функция F(U,σf) является фундаментальной частью модели Ровата-Сильверстона, поскольку она, в зависимости от значения коэффициента усиления по току σf , вызывает различное поведение осциллятора [10,11] (затухающее колебательное, потенциальное либо колебательное без затухания). Зависимость F(U,σf) может иметь линейный и нелинейный характер.

3.2 Обзор национальных и локальных источников

Для исследования используется робот-манипулятор Катана с шестью степенями свободы швейцарского производителя Neuronics. Общий вид конфигурации манипулятора Katana приведен на рис. 2. Манипулятор имеет шесть степеней свободы, каждое сочленение манипулятора – вращательное с электрическим приводом постоянного тока, соосно монтируемым с волновым редуктором Harmonic Drive. Двигатели питаются от индивидуально управляемых ШИМ-преобразователей. Система регулирования замкнутая по положению и/или по скорости двигателя. Управление электромеханическими системами отдельных суставов реализовано на базе локального контроллера робота, централизованное управление может осуществляться от компьютера, либо с помощью PLC-контроллера [12].

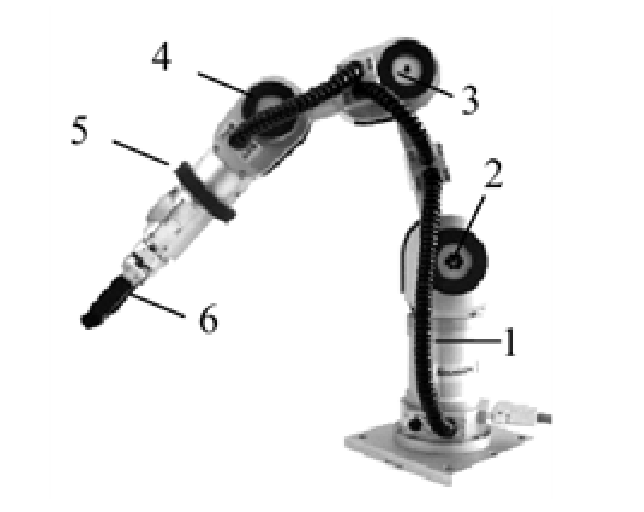
Общий вид конфигурации робота-манипулятора Катана-6М180. Картинка взята из источника 12

Рисунок 2 – Общий вид конфигурации робота-манипулятора Катана-6М180:
1 - 6 - электрические движители робота

Рекомендуемая максимальная загрузка рабочего органа робота составляет 500 г, что, учитывая высокие показатели быстродействия и точности, позволяет использовать робот в качестве интерактивного помощника при взаимодействии с человеком, а также решать ряд практических вопросов автоматизации технологического процесса (микросварка, манипуляция объектами на конвейерной линии) [12].

В статьях [13,14] разработан программно-аппаратный комплекс управления роботом-манипулятором ф. Neuronics AG. Реализован программный интерфейс на базе KNI. Создан ПИ для семейста роботов ф. Neuronics AG в симуляторе Webots и на реальном оборудовании для Katana.

4. Компьютерное моделирование нейрона

Согласно уравнениям (1) и (2) составлена модель в Simulink MATLAB (рис. 2), где для решения быстрого уравнения используем формулу (3). Значения постоянных величин принимаем следующими [9] : Af = 1; σf = 3;
τs = 1; τm = 1/20.

Составлено описание модели осциллятора на скрипт-языке Matlab. Применен метод численного интегрирования с автоматическим выбором шага ode45 [15]:

7 кадров

Анимация: 7 кадров, длительность каждого кадра - 70 мс, 165 Кб

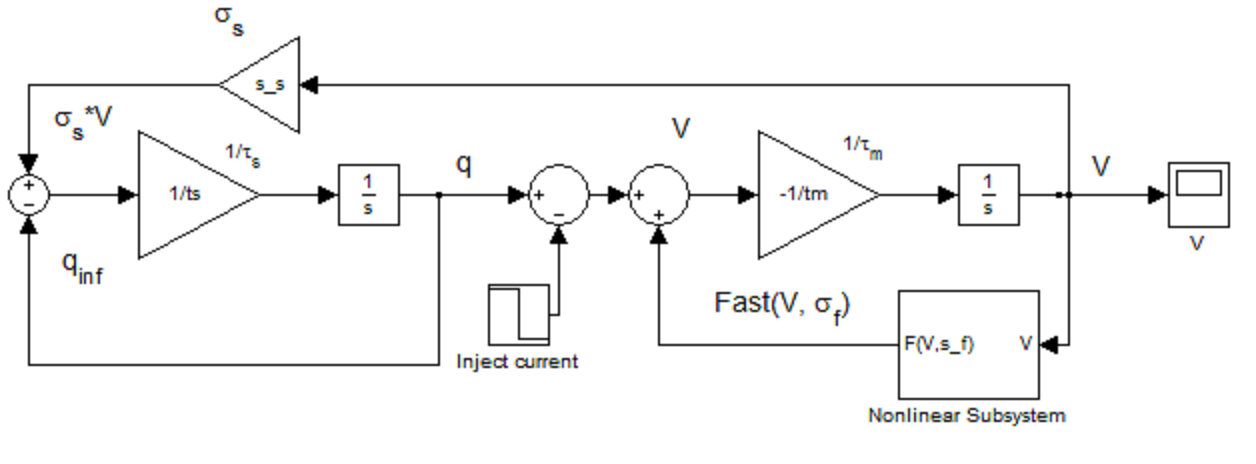
Реализация осциллятора Ровата-Сильверстона в приложении Simulink. Картинка взята из источника 15

Рисунок 3 – Реализация осциллятора Ровата-Сильверстона в приложении Simulink

Анализ результатов моделирования

С учетом вышеприведенных сведений о точности моделирования, нами были получены реакции осциллятора Ровата-Сильверстона на типовые входные воздействия. Была использована модель рис. 3. Результаты приведены на (рис. 4) [15].

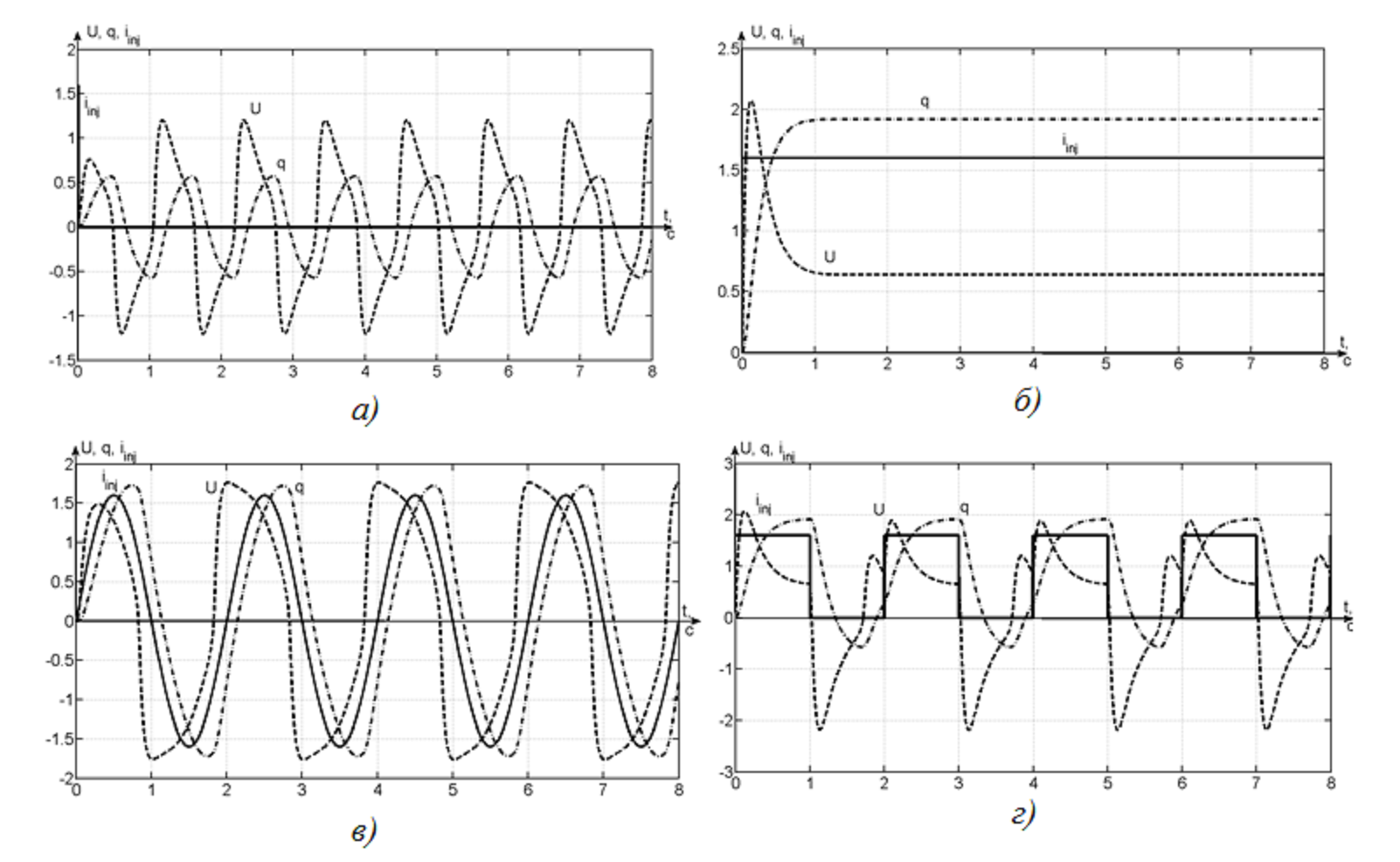
Реакция осциллятора на различные входные воздействия. Картинка взята из источника 15

Рисунок 4 – Реакция осциллятора на различные входные воздействия:
а) импульс; б) скачок; в) синусоиду (T=0,5с); г) меандр (T=0,5с)

В результате моделирования получены колебания различного характера: а) релаксационного ангармонического с частотой 1,11 Гц; б) апериодического при постоянной времени 0,25 с; в) квазигармонического при синусоидальном источнике; г) ангармонического при прямоугольных импульсах источника.

Приведенные колебания характеризуют основные режимы работы осциллятора Ровата-Сильверстона [16], отображают его свойства генерировать как апериодические сигналы, так и периодические. В данном случае синхронизация с периодическим входным воздействием (синусоида, меандр) является не типичной для биологичекских систем, где «зажиганием» нейрона упраляют дискретные импульсы тока (как в случае рис. 4.а).

Рассмотренная простая модель искусственного осциллятора не учитывает отдельные свойства своего биологического двойника – нейрона центрального генератора движений. Например, она не принимает во внимание временные задержки, которые воздействуют на динамику системы. И, что более важно, отдельный осциллятор не учитывает воздействий синхронизирующей функции биологического нейрона, которую ряд исследователей считают решающими. Последнее явление часто применяется для генерации ритмических движений антропоморфных роботов, так как моделирует естественную для человека процедуру взаимодействия с окружающей средой (жестикуляция, периодически повторяющиеся действия и т.д.). Однако, ряд работ свидетельствует, что свойством автосинхронизации обладает связанная пара осцилляторов Ровата-Сильверстона, что и есть наиболее типичный случай в биологических системах. Это будет являться предметом наших будущих исследований.

Выводы

Данная магистерская работа выполняется для усовершенствования и проверки надежности системы управления податливостью электромеханических роботов со сложной кинематикой. Предусматривается применение биологически подобных контроллеров (нелинейных осцилляторов), что позволит повысить адаптивность системы по отношению к вариации ее параметров и условий работы, что особенно важно для случая взаимодействия робота с человеком.

В реферате приводится моделирование биологически-подобного осциллятора Ровата-Сильверстона, изучение которого продолжится в дальнейшем.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2012 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Taghirad H.D., Bélanger P.R. Modeling and parameter identification of Harmonic Drive systems // Journal of Dynamic Systems, Measurements, and Control. – 22 p. [электронный ресурс]. – Режим доступа:
    http://saba.kntu.ac.ir/eecd...

  2. Tischler N. Stiffness control of robot manipulator // Proceedings 2001 ICRA IEEE International Conference on Robotics and Automation Cat No01CH37164 (2001), p. 3042 – 3046 [электронный ресурс]. – Режим доступа: http://masters.donntu.edu...

  3. Schaffer A. A., Hirzinger G. State feedback controller for flexible robots: A globally stable approach implemented on DLR’s light-weight robots // Robotics and Automation, 2007 IEEE International conference, 2007, p. 3824 – 3830 [электронный ресурс]. – Режим доступа: http://www.morpha.de/morpha_page...

  4. Luca A. D., Siciliano B., Zollo L. PD control with on-line gravity compensation for robots with elastic joints //Automatica 41(2005), 1809 – 1819.
  5. Ott C., Schaffer A. A., Kugi A. – A passivity based cartesian impedance controller for flexible joint robots – Part 1: Torque feedback and gravity compensation [электронный ресурс]. – Режим доступа: https://www.google.com...

  6. Liu G.P., Daley S. Optimal-tuning PID control for industrial systems // Control Engineering Practice 9 (2001)
    p. 1185 - 1194 [электронный ресурс]. – Режим доступа: http://www.sciencedirect.com...

  7. Bruno S., Oussama K. – Handbook of Robotics, 2008, LX, p. 7 – 9 [электронный ресурс]. – Режим доступа: http://books.google.com.ua/books...

  8. Serhan H., Nasr C. G., Henaff P. – Muscle emulation with DC motor and neural networks for biped robots // Int J Neural Syst. 2010 Aug; 20(4): 341 – 53.
  9. Rowat P.F., Selverston A.I. Oscillatory mechanisms in pairs of neurons connected with fast inhibitory synapses // Journal of Computational Neuroscience 4. – Kluwer Academic Publishers, 1997. – 25 p. [электронный ресурс]. – Режим доступа: http://crayfish.ucsd...

  10. Кузнецов А.П., Кузнецов С.П., Рыскин Н.М.  Нелинейные колебания. Учеб. пособие для вузов. – М.: Издательство физико-математической литературы, 2002. – 292 с. [электронный ресурс]. – Режим доступа: http://www.sgtnd.narod.ru...

  11. Кириллов С.Ю., Клиньшов В.В. Исследование динамических режимов модели нейрона с последеполяризацией // Труды научной конференции по радиофизике. – ННГУ, 2007. – 86 с. [электронный ресурс]. – Режим доступа: https://www.google.com/url...

  12. Мельник А.А., Хоменко В.Н., Плис П.С., П. Энафф, Борисенко В. Ф. – Кинематическая модель робота с шестью степенями свободы и возможностью учета зазора в суставах. Научные труды ДонНТУ, 10(180) 2011, 113 – 120 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal...

  13. Рябченко В.В., Дацун Н.Н.  Программно-аппаратный комплекс управления роботами-манипуляторами фирмы Neuronics AG // Материалы 4-й международной научно-технической конференции "Моделирование и компьютерная графика – 2011". Донецк, 5-8 октября 2011 г. С. 295 – 299 [электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080...

  14. Рябченко В.В., Дацун Н.Н.  Использование моделирующей среды для создания программного обеспечения программно-аппаратного комплекса управления роботом-манипулятором семейства Katana фирмы Neuronics AG // Наукові праці Донецького національного технічного університету 14 (188), 2011. – 335 – 339 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal...

  15. Snegina E., Pougatch A., Khomenko V., Melnyk A., Henaff P., Borysenko V.  Practical aspects of Rowat-Selverston
    bio-inspired oscillator simulation // Наукові праці Донецького національного технічного університету 11 (186), 2011. – 369 – 373 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal...

  16. Amrollah E., Henaff P.  On the role of sensory feedbacks in Rowat–Selverston CPG to improve robot legged locomotion // Frontiers in Neurosciences. Neurorobotics 4, 113, 2010. – 9 p. [электронный ресурс]. – Режим доступа: http://www.ncbi.nlm.nih.gov...