ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Автоматичне доведення теорем веде свій початок від основоположних робіт Ербрана, який ще в 30-х роках XX ст. запропонував механічну процедуру дедуктивного виводу. У 60-ті роки зусиллями Ньюелла і Саймона був створений загальний вирішувач проблем, що доводить теореми формальної логіки, розробленої Расселом і Уайтхедом [1], які вважали, що для математики достатньо мати формальний висновок теорем з основних аксіом.

Однак результати Черча[2] і Тьюринга[3]про нерозв'язність логіки предикатів першого порядку в якійсь мірі відтіснили роботи Ербрана на задній план. Інтерес до них зріс лише в 60-і роки, коли Гілмор реалізував ербрановську процедуру виведення на комп'ютері. Дійсно, якщо немає процедури для перевірки суперечливості (загальної значимості) формул логіки предикатів першого порядку, то найбільше, що можливо зробити - це перевірити суперечливість (загальна значимість) формули, якщо вона насправді є такою. Гілмору вдалося довести за допомогою процедури Ербрана ряд простих теорем з логіки висловлювань і логіки предикатів першого порядку, але його програма зіткнулася з нерозв'язними труднощами при доказі більш складних теорем логіки предикатів.

Ненабагато ефективнішим був метод Девіса і Патнема[4-7], за допомогою якого були доведені деякі теореми з логіки предикатів першого порядку, не доведені Гілмором. В 1964-1965 рр. незалежно один від одного з'явилися зворотний метод встановлення виводимості Маслова і принцип резолюції Робінсона[8]. У ті ж роки Шаніним[9] та його колегами було розроблено декілька версій алгоритму машинного пошуку природного логічного висновку в обчисленні висловлювань (АЛПОВ). Розробка версій системи АЛПОВ і машинних алгоритмів виводу на основі зворотнього методу і принципу резолюції показала принципову можливість машинних доказів теорем.

1. Актуальність теми

Зараз прийнято вважати, що автоматичні міркування на основі формальної логіки відносяться до слабких (weak) методів доказа теорем, і чисто синтаксичні методи управління пошуком не здатні обробляти величезний простір пошуку при вирішенні задач практичної складності. Тому альтернативою є неформальні методи пошуку, ad hoc стратегії, евристики і міркування здорового глузду, які людина використовує при вирішенні проблем.

Однак методи доведення теорем, засновані на формальній логіці типу логіки предикатів першого порядку, залишаються все ще сильною зброєю при маніпулюванні знанням і їх не можна ігнорувати. Тривалий інтерес до автоматичного доведення теорем полягає в симбіозі людини і машини при вирішенні складних проблем, коли на долю людини залишаються завдання декомпозиції складної проблеми на ряд підпроблем, пошуку потрібних евристик для скорочення простору пошуку, а автоматичному вирішувачу доводиться виконувати формальні маніпуляції зі знаннями на основі методів виводу. Яскравим прикладом використання цього симбіозу є експертні системи, засновані на правилах, що знайшли широке застосування у медицині, геології, управлінні виробництвом, транспортом, тепловими та атомними станціями і т.п.

Звичайно, домінуючий в автоматичному доказі теорем метод резолюції не є панацеєю від усіх бід, які супроводжують процедури доведення теорем, і ми маємо право сподіватися на появу досконаліших процедур дедуктивного виводу.

Магістерська робота присвячена актуальному науковому завданню розробки методу логічного висновку на графі зв'язків, який дозволить скоротити час виконання та кількість ресурсів необхідних для виконання алгоритму.

2. Мета і завдання дослідження

Метою дослідження є аналіз існуючих методів резолюції та розробка власного методу.

Основні завдання дослідження:

  1. Аналіз існуючих методів резолюції та їх евристичних функцій.
  2. Пошук способу зменшення ресурсоємності завдання за допомогою розробки власного зображення графа зв'язків.
  3. Розробка власної евристичної функції, яка дозволяє скоротити до мінімуму розростання графа при виконанні методу резолюції.

Об'єкт дослідження: логічний висновок на графі зв'язків.

Предмет дослідження: евристичні функції методу резолюції.

3. Опис області застосування

Після появи перших сучасних обчислювальних машин машинна технологія стала розвиватися з фантастичною швидкістю. Сьогодні ми бачимо, що машини використовуються не тільки для вирішення важких обчислювальних проблем таких, як виконання швидкого перетворення Фур'є або звернення матриць, високого порядку. Від них вимагають виконання і таких завдань, які були б названі інтелектуальними, якби їх робили люди. Прикладами таких задач є програмування, створення систем, що відповідають на питання, і доказ теорем. Штучний інтелект - це область обчислювальної математики, яка займається такими задачами.

Є багато завдань, які зручно перетворити у завдання доведення теорем. Перелічимо деякі з них.

  1. У питально-відповідних системах твердження можуть бути представлені логічними формулами. Тоді, щоб відповісти на запитання, використовуючи дані факти, ми доводимо, що формула, відповідна відповіді, виведена з формул, які представляють ці факти.
  2. У задачі аналізу програм ми можемо описати виконання програми формулою А, а умова, що програма закінчить роботу, іншою формулою В. Тоді перевірка того, що програма закінчить роботу, еквівалентна доказу того, що формула В випливає з формули А.
  3. У проблемі ізоморфізму графів ми хочемо знати, ізоморфний чи граф підграфу іншого графа. Ця проблема не тільки представляє математичний інтерес, ця проблема практична. Наприклад, структура органічного з'єднання може бути описана графом. Отже, перевірка того, чи є підструктура структури деякого органічного з'єднання структурою іншого органічного з'єднання, є проблема ізоморфізму. Для її вирішення ми можемо описати графи формулами. Таким чином, завдання може бути сформульована як задача докази того, що формула, яка представляє граф, випливає з формули, що представляє інший граф.
  4. У проблемі перетворення станів є набір станів і набір операторів над станами. Коли один з операторів застосовується до стану, виходить новий стан. Виходячи з початкового стану, спробуємо знайти послідовність операторів, яка перетворює початковий стан в якийсь бажаний. В цьому випадку ми можемо описати стан та правила переходу логічними формулами. Отже, перетворення початкового стану в бажаний може розглядатися як перевірка того, що формула, яка представляє бажаний стан, випливає з формули, що представляє як стан, так і правила переходу.

Метод резолюції є важливою частиною автоматичного доведення теорем. Даний метод є широко дослідженим вченими з різних кінців світу. Дослідження методу резолюції тривають і сьогодні.

4. Огляд досліджень та розробок

Метод резолюції є важливою частиною автоматичного доведення теорем. Даний метод є широко дослідженим вченими з різних кінців світу. Дослідження методу резолюції тривають і сьогодні.

4.1 Огляд міжнародних джерел

Людина здавна прагнула знайти загальну роздільну процедуру доведення теорем. Це бажання чітко простежується у Лейбніца[10] (1646—1716); воно було відроджено Пєано[11]на початку нашого століття і школою Гільберта в 20-х роках. Дуже важлива теорема була доведена Ербраном в 1930 р.: він запропонував автоматичний метод доведення теорем. На жаль, його метод був дуже важкий для реалізації, так як він був дуже трудомісткий при ручному розрахунку. З винаходом ЕОМ логіки знову проявили інтерес до автоматичного доведення теорем. У 1960-р роки теорема Ербрана була реалізована на ЕОМ Гілмором, а незабаром прослідувала більш ефективна процедура, запропонована Девісом і Патнемом.

Важливий прогрес в автоматичному доказі теорем був досягнутий Дж.А. Робінсоном в 1965 р. Він розробив єдине правило виведення - принцип резолюції, яке виявилося надзвичайно ефективним і доступним для реалізації на ЕОМ. З тих пір було запропоновано багато удосконалень принципу резолюції. Автоматичне доведення теорем додавалося в багатьох областях таких, як аналіз програм, дедуктивні системи відповідей на питання, системи вирішення завдань і технологія роботів. Число додатків продовжує зростати.

У 1945 - 1964 рр. створюються окремі програми і досліджується пошук рішення логічних задач. В Ленінграді (ЛВМІ - Ленінградське відділення математичного інституту ім. В.А. Стєклова) створюється програма, автоматично доводить теореми (АЛПЕВ ЛВМI). Вона заснована на оригінальному зворотному виведення С.Ю. Маслова, аналогічному методу резолюцій Робінсона.

У підході на основі натуральної дедукції (natural deduction), який був введений Герхардом Генценом[12] і Станіславом Яськовським, основну увагу було зосереджено не на аксіоматичних системах, а на правилах логічного висновку. Натуральна дедукція отримала назву "натуральної", оскільки в ній не потрібно перетворення в нормальну форму (незручну для сприйняття людиною), а також у зв'язку з тим, що в ній застосовуються такі правила логічного висновку, що здаються природними для людей. Правітц присвятив опису натуральної дедукції цілу книгу. Гальє застосував підхід Гентцена для роз'яснення теоретичних основ автоматизованої дедукції.

Вкрай важливим етапом в розробці глибокого математичного аналізу логіки першого порядку з'явився винахід форми подання у вигляді імплікаціонних виразів (clausal form). Уайтхед і Рассел описали так звані правила проходження (rules of passage) (фактично цей термін належить Ербрану), які використовуються для переміщення кванторів в передню частину формул. Торальф Сколем[13] досить своєчасно запропонував сколемовскі константи і сколемовскі функції. Загальна процедура сколемізаціі поряд з важливим поняттям універсуму Ербрана.

Вкрай важливу роль в розробці автоматизованих методів формування міркувань, як до, так і після введення Робінсоном правила резолюції, грає теорема Ербрана, названа на честь французького логіка Жака Ербрана. Це відбивається в застосовуваному нами терміні "універсум Ербрана", а не "універсум Сколема", навіть незважаючи на те, що це поняття в дійсності було відкрито Сколемом. Крім того, Ербран може вважатися винахідником операції уніфікації. Гедель[14], спираючись на ідеї Сколема і Ербрана, зумів показати, що для логіки першого порядку є повна процедура доказу. Алан Тьюринг і Алонсо Черч практично одночасно продемонстрували, використовуючи дуже різні докази, що задача визначення значимості в логіці першого порядку не має рішення. В чудовій книзі Ендертона[15] всі ці результати описані у чіткій, але важкодоступній для розуміння манері.

До сучасних джерел можна віднести Аверіна А.І.[16] і Вагіна В.Н.[17], які активно займаються дослідженням паралельного виводу на графі зв'язків. Також необхідно відзначити цікаву роботу Комендантської В.Є.[18]про метод резолюцій в багатозначних логіках. Слід також відзначити дослідження Асєєва І.І.[24].

4.2 Огляд національних джерел

У Київському національному університеті ім. Тараса Шевченка Лялецький А.В. і Паскевич А.Ю.[19] досліджують застосування Системи Автоматичної Дедукції для верифікації математичних текстів і мовні проблеми автоматизації доказів теорем у формалізованих теоріях.

В Національно технічному університеті України «КПІ» Асельдеров З.М. і Молчановський А.І. представили роботу по організації бази знань у системі автоматичного доведення теорем САД.

4.3 Огляд локальних джерел

В інституті штучного інтелекту та інформатики при ДонНТУ науковою роботою в області автоматичного доведення теорем займаються Грунський І.С., Козловський В.А., Барашко А.С.[20-22], Волченко М.В.[23].

5. Принцип резолюції

Основна ідея принципу резолюції полягає в перевірці, чи містить безліч диз'юнктів S порожній (помилковий) диз'юнктів ∅. Якщо це так, то S нездійсненно. Якщо S не містить ∅, то наступні кроки полягають у виведенні нових диз'юнктів до тих пір, поки не буде отриманий ∅ (що завжди буде мати місце для нездійсненного S). Таким чином, принцип резолюції розглядається як правило виведення, за допомогою якого з S породжуються нові диз'юнкти[17].

По суті принцип резолюції є розширенням Modus Ponens на випадок довільних диз'юнктів з будь-яким числом літер. Дійсно, маючи Р і Р>Q, що рівносильні ¬РvQ, можна вивести Q шляхом видалення контрарної пари Р і ¬Р. Розширення полягає в тому, що якщо будь-які два диз'юнктів С1 і С2, мають контрарні пару літер (Р і ¬Р), то, викреслюючи її, ми формуємо новий диз'юнктів з решти частин двох диз'юнктів. Цей знову сформований диз'юнктів будемо називати резольвенти диз'юнктів С1 і С2.

Розглянемо приклад. Нехай С1: Pv¬QvR, С2: ¬Pv¬Q. Тоді резольвенти С: ¬QvR.

Обґрунтованість отримання таким чином резольвенти випливає з наступної теореми: резольвенти С, отримана з двох диз'юнктів С1 і С2, є логічним наслідком цих диз'юнктів.

Якщо в процесі виведення нових диз'юнктів ми отримаємо два однолітерних диз'юнктів, що утворюють контрарні пару, то резольвенти цих двох диз'юнктів буде порожній диз'юнктів ∅. Таким чином, висновком порожнього диз'юнкта ∅ з нездійсненної безлічі диз'юнктів S називається кінцева послідовність диз'юнктів C1, С2, ..., Сk, така, що будь-Ci (i = l, k) є або диз'юнктів з S, або резольвенти, отриманої принципом резолюції , і Ck = ∅.

Висновок порожнього диз'юнктів може бути наочно представлений за допомогою дерева виводу, вершинами якого є або вихідні диз'юнктів, або резольвенти, а коренем - порожній диз'юнктів.

Розглянемо наступний приклад. Нехай S:

  1. PvQ.
  2. ¬PvQ.
  3. Pv¬Q.
  4. ¬Pv¬Q.

    5. Тоді резольвенти будуть:

  5. Q(1, 2).
  6. ¬Q(3, 4).
  7. ∅(5, 6).

Дерево висновку представлено на малюнку 1.

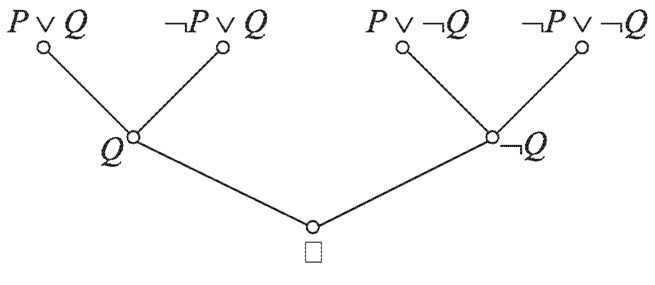
Дерево вывода

Малюнок 1 – Дерево висновку

Наведемо приклад виведення формули з безлічі посилок принципом резолюції. Нагадаємо, що доказ виведення формули G з безлічі посилок F1, F2, ..., Fn зводиться до доведення суперечливості формули F1 & F2 & ... & Fn & ¬G (процедура спростування).

Розглянемо простий приклад. Маємо наступні диз'юнкти:

  1. ¬PvQ.
  2. ¬QvR.
  3. ¬RvL.
  4. ¬Mv¬L.

    5. Заперечення висновку ¬(¬Рv¬M):

  5. P.
  6. M.

Дерево висновку представлено на малюнку 2.

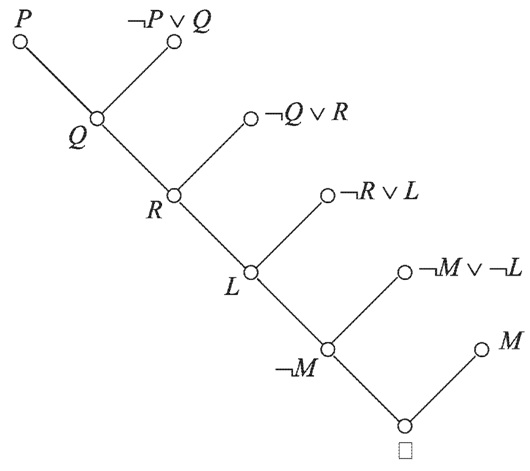
Дерево вывода

Малюнок 2 – Дерево висновку

6. Висновок на графі зв'язків

При обробці великого обсягу даних, а також при вирішенні задач, що характеризуються ростом простору пошуку, особливого значення набуває проблема ефективності процедур дедуктивного виводу.

Для ефективної роботи з множинами диз'юнктів великої потужності процедура виведення повинна відповідати наступним вимогам:

Цим умовам задовольняє процедура паралельного виводу на графі зв'язків Ковальського.

Проблема пошуку контрарних пар вирішується шляхом збереження інформації про потенційно резольвуємі предикати у графі зв'язків. Таким чином, встановлення потенційної резольвуємості проводиться один раз при створенні графа зв'язків, і немає необхідності в перегляді всієї безлічі диз'юнктів на кожному кроці резольвування - достатньо лише переглянути диз'юнкти, отримані в результаті резольвування на останньому кроці. Виняток диз'юнктів, які не можуть бути використані в доказі, досягається за допомогою простої процедури знаходження «чистих» літер. Для ефективного вибору контрарної пари можна використовувати евристичні оцінки, а також будь-які існуючі алгоритми виводу. Для організації пошуку доказів відразу за декількома напрямками процедура виведення на графі зв'язків може бути паралельна.

Розглянемо вхідну послідовність диз'юнктів: С1, С2, ..., Ck, що складаються з предикатів Р1, Р2, ..., Pi. Поставимо у відповідність кожному предикату вершину в графі зв'язків. Два вузла з'єднуються ненаправленим ребром, званим зв'язком, якщо відповідні предикати потенційно утворюють контрарну пару (що означає можливість резольвування даних предикатів після застосування до них уніфікатора та перейменування відповідних змінних). Вузли, відповідні предикатам, що належить одному диз'юнкту, групуються разом у графі зв'язків. Під час побудови графа при визначенні предикатів - потенційних кандидатів на резольвування - слід (хоча це потребуватиме додаткових обчислювальних витрат) позначити кожну зв'язок відповідним найбільш загальним уніфікатором (НОУ).

З кожним зв'язком у графі зв'язків асоціюється єдина резольвента, що є результатом резольвування предикатів, з'єднаних даним зв'язком. Після генерації резольвенти не складає особливих труднощів додати її в граф. Нові зв'язки диз'юнктів-резольвенти можуть бути обчислені з використанням наявної інформації про успадкованих зв'язках диз'юнктів-нащадків. НОУ для нових зв'язків буде являти собою композицію уніфікатора резольвування зв'язку та зв'язку диз'юнктів-предка.

Таким чином, процес резольвування для даного зв'язку являє собою отримання резольвенти, додавання резольвенти в граф зв'язків, додавання зв'язків резольвенти в граф зв'язків і видалення «старих» зв'язків і диз'юнктів з графа зв'язків.

Видалення «старих» зв'язків і диз'юнктів проводиться за такою схемою:

  1. Коли резольвенти генеровані і додані в граф, зв'язок, який породив резольвенту, видаляється з графа зв'язків.
  2. Якщо вершина не має зв'язків, то диз'юнкт, якому ця вершина (предикат) належить, видаляється з графа разом з усіма зв'язками.
  3. Якщо диз'юнкт є тавтологією, то він видаляється з усіма належними йому предикатами і зв'язками.

Значною мірою гнучкість і міць процедури висновку є наслідком її недетермінізму, так як на кожному кроці алгоритму може бути обран будь-який зв'язок для резольвування. Для точного визначення процедури виведення необхідно звернути увагу на деталі, особливо на питання, пов'язані з факторизацією, поглинанням диз'юнктів, видаленням диз'юнктів-тавтологій і чистих диз'юнктів.

Таким чином, послідовний алгоритм виведення на графі зв'язків має наступний вигляд:

  1. Вибір зв'язку з безлічі зв'язків.
  2. Резольвування зв'язку та отримання резольвенти. Видалення зв'язку, за яким проводилося резольвування.
  3. Якщо отримана порожня резольвента, то успішне завершення, інакше приміщення резольвенти в граф, додавання її зв'язків, видалення диз'юнктів-тавтологій і чистих диз'юнктів, виконання операцій факторизації та поглинання диз'юнктів.
  4. Якщо граф не містить жодного диз'юнкта, то неуспішне завершення алгоритму, інакше перехід до кроку 1.

Розглянемо приклад. Існують студенти, які люблять всіх викладачів. Жоден із студентів не любить невігласів. Отже, жоден із викладачів не є невігласом.

Розглянемо основні кроки алгоритму (малюнок 3). На першому кроці проводиться вибір зв'язку для резольвування і резольвування обраного зв'язку. Прорезольвований зв'язок видаляється. Виберемо для резольвування зв'язок 1.

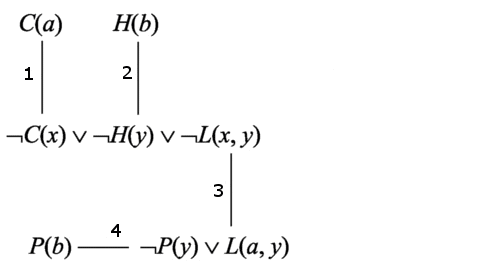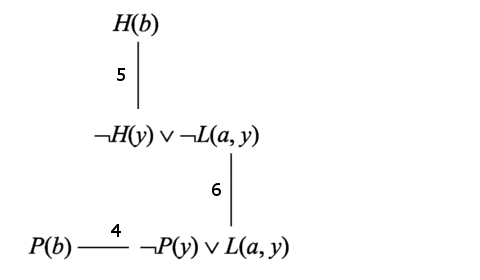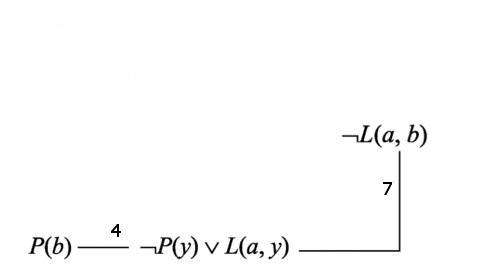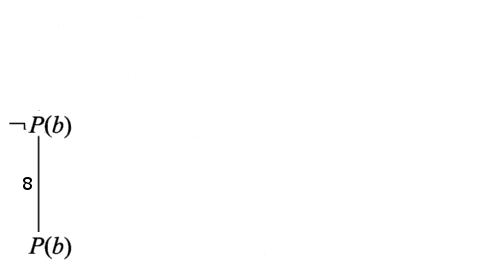
Диаграмма состояний автомата Мура

Малюнок 3 – Приклад алгоритму логічного висновку на графі зв'язків
(анімація: 7 кадрів, 7 циклів, 18 КБ)

На другому кроці відбувається резольвування по цьому зв'язку, в результаті якого ми отримуємо диз'юнкт 6: ¬ Н (у) v ¬ L (a, y). Видаляємо зв'язок 1 і переходимо до кроку 3 алгоритму.

На третьому кроці перевіряємо, чи є отриманий на попередньому кроці диз'юнкт порожнім. Так як диз'юнкт 6 не є порожнім диз'юнктом, додаємо його в граф зв'язків. Також додаємо зв'язок диз'юнкту 6.

Диз'юнкти С (а) і ¬ С (х) v ¬ Н (у) v ¬ L (x, y) містять чисті літери С (а) і ¬ C (x), тобто є чистими диз'юнктами і підлягають видаленню з графа зв'язків . Після видалення даних диз'юнктів отримуємо граф зв'язків.

Даний граф зв'язків не містить диз'юнктів-тавтологій і чистих диз'юнктів, що підлягають видаленню. Операції факторизації та поглинання диз'юнктів також є непридатними до даної безлічі диз'юнктів, тому переходимо до кроку 4 алгоритму.

Граф зв'язків, не містить порожнього диз'юнкта, тому переходимо до кроку 1.

Виберемо для резольвування зв'язок 5. Після резольвування по цьому зв'язку отримуємо диз'юнкт 7: ¬ L (a, b). Видаляємо зв'язок 5 і переходимо до кроку 4 алгоритму.

Диз'юнкт 7 не є порожнім диз'юнктом, тому додаємо його в граф зв'язків. Також додаємо зв'язок диз'юнкту 7.

Диз'юнкти Н (b) і ¬ H (y) v ¬ L (a, y) містять чисті літери Н (b) і ¬ Н (у), тобто є чистими диз'юнктами і підлягають видаленню з графа зв'язків. Після видалення даних диз'юнктів отримуємо граф зв'язків.

Даний граф зв'язків не містить диз'юнктів-тавтологій і чистих диз'юнктів, що підлягають видаленню. Операції факторизації та поглинання диз'юнктів також є непридатними до даної безлічі диз'юнктів, тому переходимо до кроку 4 алгоритму.

Граф зв'язків містить диз'юнкти, тому переходимо до кроку 1.

Виберемо для резольвування зв'язок 7. Після резольвування по цьому зв'язку отримуємо диз'юнкт 8: ¬ Р (b). Видаляємо зв'язок 7 і переходимо до кроку 3 алгоритму.

Диз'юнкт 8 не є порожнім диз'юнктом, тому додаємо його в граф зв'язків. Також додаємо зв'язки диз'юнкта 8. Диз'юнкти ¬ L (a, b) і ¬ Р (у) v L (a, y) містять чисті літери ¬ L (a, b) і L (a, b), тобто є чистими диз'юнктами і підлягають видаленню з графа зв'язків . Після видалення даних диз'юнктів отримуємо граф зв'язків.

Даний граф зв'язків не містить диз'юнктів-тавтологій і чистих диз'юнктів, що підлягають видаленню. Операції факторизації та поглинання диз'юнктів також є непридатними до даної безлічі диз'юнктів, тому переходимо до кроку 4 алгоритму.

Граф зв'язків містить диз'юнкти, тому переходимо до кроку 1.

Виберемо для резольвування зв'язок 8. Після резольвування по цьому зв'язку отримуємо диз'юнкт 9: ∅. Видаляємо зв'язок 8 і переходимо до кроку 3 алгоритму.

Диз'юнкт 9 є порожнім диз'юнктом, отже вихідна безліч диз'юнктів - нездійсненна. Завершення роботи алгоритму.

Доведена повнота і спроможність процедури виведення на графі зв'язків. Вищенаведений алгоритм є недетермінованим.

Для реалізації його на детермінованій машині він потребує детерміновану процедуру вибору резольвуємого зв'язку. В даному питанні можливе використання декількох основних методик, наприклад, вибір зв'язку, активація якої призведе до зменшення кількості диз'юнктів в графі, кількості зв'язків чи кількості входжень предикатів в диз'юнкт. Ідеальна ситуація виникає у разі, коли зв'язок з'єднує пару предикатів, які не мають жодних інших зв'язків. Також до спрощення графа призводить злиття однакових предикатів у диз'юнкти-батьки. Ще одним фактором, що впливає на вибір зв'язку, є єдність зв'язку для предиката, що призводить, як сказано раніше, до видалення диз'юнктів, що містить цей предикат після резольвування. У випадку, коли спрощення графа домогтися не вдається, слід вибрати зв'язок, резольвування якого призведе до мінімального ускладнення графа зв'язків. У цій ситуації слід віддавати перевагу зв'язкам, резольвенти яких містять найменшу кількість предикатів.

Висновки

Оскільки багато завдань можуть бути сформульовані як задачі доказу теорем, проблема автоматизації доказів є важливою у штучному інтелекті. Завдяки невпинним зусиллям багатьох дослідників був досягнутий великий прогрес у використанні машин для доведення теорем.

Магістерська робота присвячена актуальній науковій розробки алгоритму логічного висновку на графі зв'язків. У рамках проведених досліджень виконано:

  1. Виділено ключові особливості методу резолюції на графі зв'язків.
  2. Розглянуто можливість створення оптимальної евристики.
  3. Проведено ряд експериментів з удосконалення подання графа зв'язків для зменшення ресурсоємності алгоритму.

Подальші дослідження спрямовані на такі аспекти:

  1. Створення оптимальної евристичної функції для методу резолюції на графі зв'язків.
  2. Розбиття графа зв'язків на підграфи для зменшення часу виконання алгоритму.
  3. Розробка демонстраційної системи, що реалізує запропонований у магістерській роботі алгоритм методу резолюції.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Перелік посилань

  1. Уайтхед А.Н. Основания математики: в 3 т. / Альфред Н. Уайтхед, Бертран Рассел; пер. с англ. Ю.Н. Радаева, И.С. Фролова; под ред. Г.П. Ярового, Ю.Н. Радаева. – Самара: Книга, 2005–2006. – 234 c.
  2. Alonzo Church, A Bibliography of Symbolic Logic, 1666–1935. – 164 pp.
  3. Alan M. Turing – Collected works of A. M. Turing. Mathematical logic. Elsevier, Amsterdam, The Netherlands, 2001. – 745 pp.
  4. Патнэм Х. Философия сознания / Пер. с англ. Л. Б. Макеевой, О. А. Назаровой, А. Л. Никифорова; предисл. Л. Б. Макеевой. М.: Дом интеллектуальной книги, 1999. 240 с.
  5. Патнэм Х. Разум, истина и история / Пер. с англ. Т.А. Дмитриева, М.В. Лебедева. – М.: Праксис, 2002. – 296 с.
  6. Патнэм Х. Как нельзя говорить о значении (комментарий к статье Дж. Дж. Смарта) // Структура и развитие науки. М., 1978. С. 396–418
  7. Патнэм Х. Значение и референция // Новое в зарубежной лингвистике. Вып. 13. М., 1982. С. 377–390.
  8. Робинсон А. Введение в теорию моделей и мета–математику алгебры. // Серия «Математическая логика и основания математики». М.: Наука, 1967, 378 с.
  9. Шанин Н.А. Алгорифм машинного поиска естественного логического вывода в исчислении высказываний // М.: Наука, 1965, 38 с.
  10. Лейбниц Г. В. Математические работы в переводе А. П. Юшкевича // Успехи Мат. Наук, – М.: Наука, 2003. – 235 с.
  11. Peano G. "The principles of arithmetic, presented by a new method" in Jean van Heijenoort, 1967. A Source Book in Mathematical Logic, 1879–1931. Harvard Univ. pp. 83–97.
  12. Генцен Г. Непротиворечивость чистой теории чисел. // Математическая теория логического вывода. М.: Наука, 1967, C. 77–153.
  13. Skolem, Th. (1934) Uber die Nicht–charakterisierbarkeit der Zahlenreihe mittels endlich oder abzahlbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen. Fundam. Math. 23, pp. 150–161.
  14. John W. Dawson, Jr. Logical Dilemmas: The Life and Work of Kurt Godel. AK Peters, Ltd., 1996. – 247 pp.
  15. Enderton H.B. A Mathematical Introduction to Logic // 2nd ed., Academic Press, 2001. 326 pp.
  16. Аверин А.И., Вагин В.Н. Параллелизм в дедуктивном выводе на графовых структурах,Автомат. и телемех., 2001, № 10. C. 54–64.
  17. Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фомина М.В. Достоверный и правдоподобный вывод в интеллектуальных системах Монография. Под ред. В.Н. Вагина и Д.А.Поспелова. М.: Изд. 2–ое исправл. и дополн. Физматлит, 2008, 714 с.
  18. Комендантский В.Е. Метод резолюций в смешанной логике Поста // Труды XVI научно–исследовательского семинара логического центраИФРАН. М.: ИФРАН, 2002. С. 64–74.
  19. Анисимов А.В., Вершинин К.П., Лялецкий А.В., Паскевич А.Ю. //Система автоматизации дедукции (САД) как средство обработки формальных компьютерных заданий . The Fourth International Conference Theoretical and Applied Aspects of Program Systems Development (TAAPSD’2007). Abstracts (4–9 September, 2007, Berdyansk, Ukraine), Київ, Р. 9–14.
  20. Богомолов А.М., Барашко А.С., Грунский И.С. Эксперименты с автоматами. – Киев: Наукова думка, 1973. – 144 с.
  21. Богомолов А.М., Грунский И.С., Сперанский Д.В. Контроль и преобразование дискретных автоматов. – Киев: Наукова думка, 1975. – 176 с.
  22. Грунский И.С., Козловский В.А. Синтез и идентификация автоматов. – Киев: Наукова думка, 2004. – 246 с.
  23. Волченко М.В. Представление термов для алгоритма резолюции логики высказываний. Информатики и компьютерные технологии / Материалы V международной конференции. – Донецк: Изд–во ДГТУ, 2009.
  24. Асеев И.И. – Алгебра степенных операторов [Электронный ресурс]. – Режим доступа: http://sceptic-ratio.narod.ru/ma.htm