ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

Автоматическое доказательство теорем ведет свое начало от основополагающих работ Эрбрана, который еще в 30-х годах XX в. предложил механическую процедуру дедуктивного вывода. В 60-е годы усилиями Ньюэлла и Саймона был создан общий решатель проблем, доказывающий теоремы формальной логики, разработанной Расселом и Уайтхедом[1], которые считали, что для математики достаточно иметь формальный вывод теорем из основных аксиом.

Однако результаты Чёрча[2] и Тьюринга[3] о неразрешимости логики предикатов первого порядка в какой-то степени оттеснили работы Эрбрана на задний план. Интерес к ним возрос лишь в 60-е годы, когда Гилмор реализовал эрбрановскую процедуру вывода на компьютере. Действительно, если нет процедуры для проверки противоречивости (общезначимости) формул логики предикатов первого порядка, то самое большее, что можно сделать – это проверить противоречивость (общезначимость) формулы, если она на самом деле таковой и является. Гилмору удалось доказать с помощью процедуры Эрбрана ряд простых теорем из логики высказываний и логики предикатов первого порядка, но его программа столкнулась с неразрешимыми трудностями при доказательстве более сложных теорем логики предикатов.

Ненамного эффективнее был метод Девиса и Патнема[4-7], с помощью которого были доказаны некоторые теоремы из логики предикатов первого порядка, не доказанные Гилмором. В 1964-1965 гг. независимо друг от друга появились обратный метод установления выводимости Маслова и принцип резолюции Робинсона[8]. В те же годы Шаниным[9] и его коллегами было разработано несколько версий алгоритма машинного поиска естественного логического вывода в исчислении высказываний (АЛПЕВ). Разработка версий системы АЛПЕВ и машинных алгоритмов вывода на основе обратного метода и принципа резолюции показала принципиальную возможность машинных доказательств теорем.

1. Актуальность темы

Сейчас принято считать, что автоматические рассуждения на основе формальной логики относятся к слабым (weak) методам доказательства теорем, и чисто синтаксические методы управления поиском не способны обрабатывать огромное пространство поиска при решении задач практической сложности. Поэтому альтернативой являются неформальные методы поиска, ad hoc стратегии, эвристики и рассуждения здравого смысла, которые человек использует при решении проблем.

Однако методы доказательства теорем, основанные на формальной логике типа логики предикатов первого порядка, остаются все еще сильным оружием при манипулировании знанием и их нельзя игнорировать. Продолжающийся интерес к автоматическому доказательству теорем заключается в симбиозе человека и машины при решении сложных проблем, когда на долю человека остаются задачи декомпозиции сложной проблемы на ряд подпроблем, поиска нужных эвристик для сокращения пространства поиска, а автоматическому решателю доводится выполнять формальные манипуляции со знанием на основе методов вывода. Ярким примером использования этого симбиоза являются экспертные системы, основанные на правилах, нашедшие широкое применение в медицине, геологии, управлении производством, транспортом, тепловыми и атомными станциями и т.п.

Конечно, доминирующий в автоматическом доказательстве теорем метод резолюции не является панацеей от всех бед, сопровождающих процедуры доказательства теорем, и мы вправе надеяться на появление более совершенных процедур дедуктивного вывода.

Магистерская работа посвящена актуальной научной задаче разработки логического вывода на графе связей, который позволит сократить время выполнения и количество ресурсов необходимых для выполнения алгоритма.

2. Цель и задачи исследования

Целью исследования является анализ существующих методов резолюции и разработка собственного метода.

Основные задачи исследования:

  1. Анализ существующих методов резолюции и их эвристических функций.
  2. Поиск способа уменьшения ресурсоемкости задачи с помощью разработки собственного представления графа связей.
  3. Разработка собственной эвристической функции позволяющей сократить до минимума разрастание графа при выполнении метода резолюции.

Объект исследования: логический вывод на графе связей.

Предмет исследования: эвристические функции метода резолюции.

3. Описание области применения

После появления первых современных вычислительных машин машинная технология стала развиваться с фантастической скоростью. Сегодня мы видим, что машины используются не только для решения трудных вычислительных проблем таких, как выполнение быстрого преобразования Фурье или обращение матриц, высокого порядка. От них требуют выполнения и таких задач, которые были бы названы интеллектуальными, если бы их делали люди. Примерами таких задач являются программирование, создание систем, отвечающих на вопросы, и доказательство теорем. Искусственный интеллект – это область вычислительной математики, которая занимается такими задачами.

Есть много задач, которые удобно преобразовать в задачи доказательства теорем. Перечислим некоторые из них.

  1. В вопросно-ответных системах утверждения могут быть представлены логическими формулами. Тогда, чтобы ответить на вопрос, используя данные факты, мы доказываем, что формула, соответствующая ответу, выводима из формул, представляющих эти факты.
  2. В задаче анализа программ мы можем описать выполнение программы формулой А, а условие, что программа закончит работу, другой формулой В. Тогда проверка того, что программа закончит работу, эквивалентна доказательству того, что формула В следует из формулы А.
  3. В проблеме изоморфизма графов мы хотим знать, изоморфен ли граф подграфу другого графа. Эта проблема не только представляет математический интерес, эта проблема практическая. Например, структура органического соединения может быть описана графом. Следовательно, проверка того, является ли подструктура структуры некоторого органического соединения структурой другого органического соединения, есть проблема изоморфизма. Для ее решения мы можем описать графы формулами. Таким образом, задача может быть сформулирована как задача доказательства того, что формула, представляющая граф, следует из формулы, представляющей другой граф.
  4. В проблеме преобразования состояний имеется набор состояний и набор операторов над состояниями. Когда один из операторов применяется к состоянию, получается новое состояние. Исходя из начального состояния, попытаемся найти последовательность операторов, которая преобразует начальное состояние в некоторое желаемое. В этом случае мы можем описать состояния и правила перехода логическими формулами. Следовательно, преобразование начального состояния в желаемое может рассматриваться как проверка того, что формула, представляющая желаемое состояние, следует из формулы, представляющей как состояния, так и правила перехода.

Поскольку многие задачи могут быть сформулированы как задачи доказательства теорем, проблема автоматизации доказательств оказывается важной областью в искусственном интеллекте.

4. Обзор исследований и разработок

Метод резолюции является важной частью автоматического доказательства теорем. Данный метод является широко исследованным учеными с разных концов мира. Исследование метода резолюции продолжаются и сегодня.

4.1 Обзор международных источников

Человек издавна стремился найти общую разрешающую процедуру доказательства теорем. Это желание четко прослеживается у Лейбница[10] (1646—1716); оно было воскрешено Пеано[11] в начале нашего столетия и школой Гильберта в 20-х годах. Очень важная теорема была доказана Эрбраном в 1930 г.: он предложил автоматический метод доказательства теорем. К сожалению, его метод был весьма труден для реализации, так как он был весьма трудоемок при ручном счете. С изобретением ЭВМ логики снова проявили интерес к автоматическому доказательству теорем. В 1960е годы теорема Эрбрана была реализована на ЭВМ Гилмором, а вскоре последовала более эффективная процедура, предложенная Девисом и Патнемом.

Важный прогресс в автоматическом доказательстве теорем был достигнут Дж.А. Робинсоном в 1965 г. Он разработал единственное правило вывода — принцип резолюции, которое оказалось чрезвычайно эффективным и легкодоступным для реализации на ЭВМ. С тех пор было предложено много усовершенствований принципа резолюции. Автоматическое доказательство теорем прилагалось во многих областях таких, как анализ программ, дедуктивные системы ответов на вопросы, системы решения задач и технология роботов. Число приложений продолжает расти.

В 1945 - 1964 гг. создаются отдельные программы и исследуется поиск решения логических задач. В Ленинграде (ЛОМИ — Ленинградское отделение математического института им. В.А. Стеклова) создается программа, автоматически доказывающая теоремы (АЛПЕВ ЛОМИ). Она основана на оригинальном обратном выводе С.Ю. Маслова, аналогичном методу резолюций Робинсона.

В подходе на основе натуральной дедукции (natural deduction), который был введен Герхардом Генценом[12] и Станиславом Яськовским, основное внимание было сосредоточено не на аксиоматических системах, а на правилах логического вывода. Натуральная дедукция получила название "натуральной", поскольку в ней не требуется преобразование в нормальную форму (неудобную для восприятия человеком), а также в связи с тем, что в ней применяются такие правила логического вывода, которые кажутся естественными для людей. Правитц посвятил описанию натуральной дедукции целую книгу. Галье применил подход Гентцена для разъяснения теоретических основ автоматизированной дедукции.

Крайне важным этапом в разработке глубокого математического анализа логики первого порядка явилось изобретение формы представления в виде импликационных выражений (clausal form). Уайтхед и Рассел описали так называемые правила прохождения (rules of passage) (фактически этот термин принадлежит Эрбрану), которые используются для перемещения кванторов в переднюю часть формул. Торальфом Сколемом[13] были достаточно своевременно предложены сколемовские константы и сколемовские функции. Общая процедура сколемизации, наряду с важным понятием универсума Эрбрана.

Крайне важную роль в разработке автоматизированных методов формирования рассуждений, как до, так и после введения Робинсоном правила резолюции, играет теорема Эрбрана, названная в честь французского логика Жака Эрбрана. Это отражается в применяемом нами термине "универсум Эрбрана", а не "универсум Сколема", даже несмотря на то, что это понятие в действительности было открыто Сколемом. Кроме того, Эрбран может считаться изобретателем операции унификации. Гёдель[14], опираясь на идеи Сколема и Эрбрана, сумел показать, что для логики первого порядка имеется полная процедура доказательства. Алан Тьюринг и Алонсо Черч практически одновременно продемонстрировали, используя очень разные доказательства, что задача определения общезначимости в логике первого порядка не имеет решения. В превосходной книге Эндертона[15] все эти результаты описаны в строгой, но труднодоступной для понимания манере.

К современным источникам можно отнести Аверина А.И.[16] и Вагина В.Н. [17] активно занимающихся исследованием параллельного вывода на графе связей. Также необходимо отметить интересную работу Комендантского В.Е.[18] о методе резолюций в многозначных логиках. Следует также отметить исследование Асеева И.И.[24].

4.2 Обзор национальных источников

В Киевском национальном университете им. Тараса Шевченко Лялецкий А.В. и Паскевич А.Ю.[19] исследуют применение Системы Автоматической Дедукции для верификации математических текстов и языковые проблемы автоматизации доказательств теорем в формализованных теориях.

В Национально техническом университете Украины «КПИ» Асельдеров З.М. и Молчановский А.И. представили работу по организации базы знаний в системе автоматического доказательства теорем САД.

4.3 Обзор локальных источников

В институте искусственного интеллекта и информатики при ДонНТУ научной работой в области автоматического доказательства теорем занимаются Грунский И.С., Козловский В.А., Барашко А.С.[20-22], Волченко М.В.[23] и др.

5. Принцип резолюции

Основная идея принципа резолюции заключается в проверке, содержит ли множество дизъюнктов S пустой (ложный) дизъюнкт ∅. Если это так, то S невыполнимо. Если S не содержит ∅, то следующие шаги заключаются в выводе новых дизъюнктов до тех пор, пока не будет получен ∅ (что всегда будет иметь место для невыполнимого S). Таким образом, принцип резолюции рассматривается как правило вывода, с помощью которого из S порождаются новые дизъюнкты[17].

По существу принцип резолюции является расширением Modus Ponens на случай произвольных дизъюнктов с любым числом литер. Действительно, имея Р и Р > Q, что равносильно ¬Р v Q, можно вывести Q путем удаления контрарной пары Р и ¬Р. Расширение состоит в том, что если любые два дизъюнкта С1 и С2, имеют контрарную пару литер (Р и ¬Р), то, вычеркивая ее, мы формируем новый дизъюнкт из оставшихся частей двух дизъюнктов. Этот вновь сформированный дизъюнкт будем называть резольвентой дизъюнктов С1 и С2.

Рассмотрим пример. Пусть С1: P v ¬Q v R, С2: ¬P v ¬Q. Тогда резольвента С: ¬QvR.

Обоснованность получения таким образом резольвенты вытекает из следующей теоремы: резольвента С, полученная из двух дизъюнктов С1 и С2, является логическим следствием этих дизъюнктов.

Если в процессе вывода новых дизъюнктов мы получим два однолитерных дизъюнкта, образующих контрарную пару, то резольвентой этих двух дизъюнктов будет пустой дизъюнкт ∅. Таким образом, выводом пустого дизъюнкта ∅ из невыполнимого множества дизъюнктов S называется конечная последовательность дизъюнктов C1, С2,..., Сk, такая, что любой Ci (i = l, k) является или дизъюнктом из S, или резольвентой, полученной принципом резолюции, и Ck = ∅.

Вывод пустого дизъюнкта может быть наглядно представлен с помощью дерева вывода, вершинами которого являются или исходные дизъюнкты, или резольвенты, а корнем – пустой дизъюнкт.

Рассмотрим следующий пример. Пусть S:

  1. P v Q.
  2. ¬P v Q.
  3. P v ¬ Q.
  4. ¬P v ¬Q.

    5. Тогда резольвенты будут:

  5. Q(1, 2).
  6. ¬Q(3, 4).
  7. ∅(5, 6).

Дерево вывода представлено на рисунке 1.

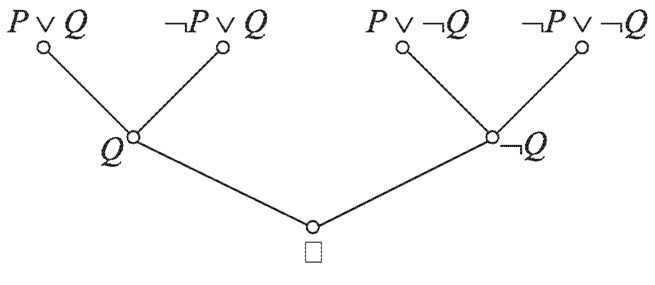
Дерево вывода

Рисунок 1 – Дерево вывода

Приведем пример вывода формулы из множества посылок принципом резолюции. Напомним, что доказательство вывода формулы G из множества посылок F1, F2,…, Fn сводится к доказательству противоречивости формулы F1 & F2 & ... & Fn & ¬G (процедура опровержения).

Рассмотрим простой пример. Имеем следующее множество дизъюнктов:

  1. ¬P v Q.
  2. ¬Q v R.
  3. ¬R v L.
  4. ¬M v ¬L.

    5. Oтрицание заключения ¬(¬Р v ¬M):

  5. P.
  6. M.

Дерево вывода представлено на рисунке 2.

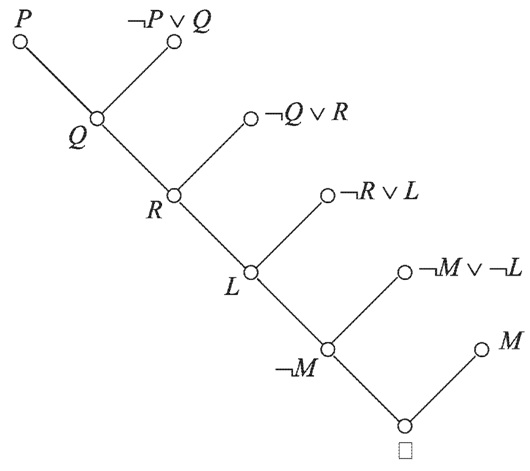
Дерево вывода

Рисунок 2 – Дерево вывода

6. Вывод на графе связей

При обработке большого объема данных, а также при решении задач, характеризующихся экспоненциальным ростом пространства поиска, особое значение приобретает проблема эффективности процедур дедуктивного вывода.

Для эффективной работы с множествами дизъюнктов большой мощности процедура вывода должна отвечать следующим требованиям:

Этим условиям удовлетворяет процедура параллельного вывода на графе связей Ковальского.

Проблема поиска контрарных пар решается путем сохранения информации о потенциально резольвируемых предикатах в графе связей. Таким образом, установление потенциальной резольвируемости производится один раз при создании графа связей, и нет необходимости в просмотре всего множества дизъюнктов на каждом шаге резольвирования – достаточно лишь просмотреть дизъюнкты, полученные в результате резольвирования на последнем шаге. Исключение дизъюнктов, которые не могут быть использованы в доказательстве, достигается с помощью простой процедуры нахождения «чистых» литер. Для эффективного выбора контрарной пары можно использовать эвристические оценки, а также любые существующие алгоритмы вывода. Для организации поиска доказательства сразу по нескольким направлениям процедура вывода на графе связей может быть распараллелена.

Рассмотрим исходную последовательность дизъюнктов: С1, С2,..., Ck, состоящих из предикатов Р1, Р2,..., Pi. Поставим в соответствие каждому предикату вершину в графе связей. Два узла соединяются ненаправленным ребром, называемым связью, если соответствующие предикаты потенциально образуют контрарную пару (что означает возможность резольвирования данных предикатов после применения к ним унификатора и переименования соответствующих переменных). Узлы, соответствующие предикатам, принадлежащим одному дизъюнкту, группируются вместе в графе связей. Во время построения графа при определении предикатов – потенциальных кандидатов на резольвирование – следует (хотя это потребует дополнительных вычислительных затрат) пометить каждую связь соответствующим наиболее общим унификатором (НОУ).

С каждой связью в графе связей ассоциируется единственная резольвента, являющаяся результатом резольвирования предикатов, соединенных данной связью. После генерации резольвенты не составляет особого труда добавить ее в граф. Новые связи дизъюнкта-резольвенты могут быть вычислены с использованием имеющейся информации о наследуемых связях дизъюнктов-потомков. НОУ для новых связей будет представлять собой композицию унификатора резольвированной связи и связи дизъюнкта-предка.

Таким образом, процесс резольвирования для данной связи представляет собой получение резольвенты, добавление резольвенты в граф связей, добавление связей резольвенты в граф связей и удаление «старых» связей и дизъюнктов из графа связей.

Удаление «старых» связей и дизъюнктов производится по следующей схеме:

  1. Когда резольвента сгенерирована и добавлена в граф, связь, которая породила резольвенту, удаляется из графа связей.
  2. Если вершина не имеет связей, то дизъюнкт, которому эта вершина (предикат) принадлежит, удаляется из графа вместе со всеми связями.
  3. Если дизъюнкт является тавтологией, то он удаляется со всеми принадлежащими ему предикатами и связями.

В значительной мере гибкость и мощь процедуры вывода является следствием ее недетерминизма, так как на каждом шаге алгоритма может быть выбрана любая связь для резольвирования. Для точного определения процедуры вывода необходимо обратить внимание на детали, особенно на вопросы, связанные с факторизацией, поглощением дизъюнктов, удалением дизъюнктов-тавтологий и чистых дизъюнктов.

Таким образом, последовательный алгоритм вывода на графе связей имеет следующий вид:

  1. Выбор связи из множества связей.
  2. Резольвирование связи и получение резольвенты. Удаление связи, по которой производилось резольвирование.
  3. Если получена пустая резольвента, то успешное завершение, иначе помещение резольвенты в граф, добавление ее связей, удаление дизъюнктов-тавтологий и чистых дизъюнктов, выполнение операций факторизации и поглощения дизъюнктов.
  4. Если граф не содержит ни одного дизъюнкта, то неуспешное завершение алгоритма, иначе переход к шагу 1.

Рассмотрим пример. Существуют студенты, которые любят всех преподавателей. Ни один из студентов не любит невежд. Следовательно, ни один из преподавателей не является невеждой.

Рассмотрим основные шаги алгоритма (рис. 3). На первом шаге производится выбор связи для резольвирования и резольвирование выбранной связи. Прорезольвированная связь удаляется. Выберем для резольвирования связь 1.

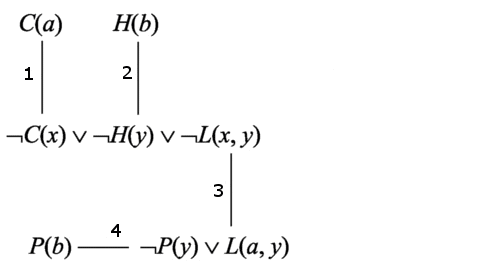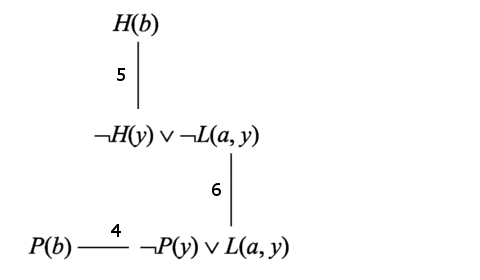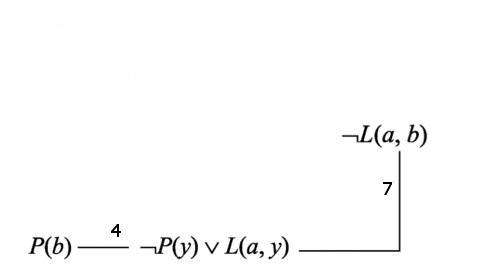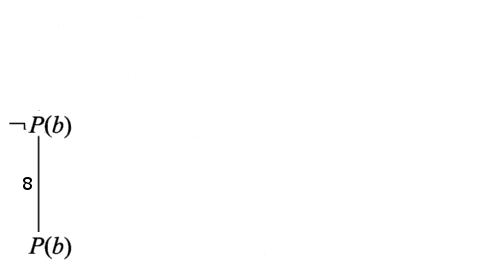
Диаграмма состояний автомата Мура

Рисунок 3 – Пример алгоритма логического вывода на графе связей
(анимация: 7 кадров, 7 циклов повторения, 18 килобайт)

На втором шаге происходит резольвирование по этой связи, в результате которого мы получаем дизъюнкт 6: ¬Н(у) v ¬L(a, y). Удаляем связь 1 и переходим к шагу 3 алгоритма.

На третьем шаге проверяем, является ли полученный на предыдущем шаге дизъюнкт пустым. Так как дизъюнкт 6 не является пустым дизъюнктом, добавляем его в граф связей. Также добавляем связи дизъюнкта 6.

Дизъюнкты С(а) и ¬С(х) v ¬Н(у) v ¬L(x,y) содержат чистые литеры С(а) и ¬C(x), то есть являются чистыми дизъюнктами и подлежат удалению из графа связей. После удаления данных дизъюнктов получаем граф связей.

Данный граф связей не содержит дизъюнктов-тавтологий и чистых дизъюнктов, подлежащих удалению. Операции факторизации и поглощения дизъюнктов также являются неприменимыми к данному множеству дизъюнктов, поэтому переходим к шагу 4 алгоритма.

Граф связей, не содержит пустого дизъюнкта, поэтому переходим к шагу 1.

Выберем для резольвирования связь 5. После резольвирования по этой связи получаем дизъюнкт 7: ¬L(a, b). Удаляем связь 5 и переходим к шагу 4 алгоритма.

Дизъюнкт 7 не является пустым дизъюнктом, поэтому добавляем его в граф связей. Также добавляем связи дизъюнкта 7.

Дизъюнкты Н(b) и ¬H(y) v ¬L(a, y) содержат чистые литеры Н(b) и ¬Н(у), то есть являются чистыми дизъюнктами и подлежат удалению из графа связей. После удаления данных дизъюнктов получаем граф связей.

Данный граф связей не содержит дизъюнктов-тавтологий и чистых дизъюнктов, подлежащих удалению. Операции факторизации и поглощения дизъюнктов также являются неприменимыми к данному множеству дизъюнктов, поэтому переходим к шагу 4 алгоритма.

Граф связей, содержит дизъюнкты, поэтому переходим к шагу 1.

Выберем для резольвирования связь 7. После резольвирования по этой связи получаем дизъюнкт 8: ¬Р(b). Удаляем связь 7 и переходим к шагу 3 алгоритма.

Дизъюнкт 8 не является пустым дизъюнктом, поэтому добавляем его в граф связей. Также добавляем связи дизъюнкта 8. Дизъюнкты ¬L(a, b) и ¬Р(у) v L(a, y) содержат чистые литеры ¬L(a, b) и L(a, b), то есть являются чистыми дизъюнктами и подлежат удалению из графа связей. После удаления данных дизъюнктов получаем граф связей.

Данный граф связей не содержит дизъюнктов-тавтологий и чистых дизъюнктов, подлежащих удалению. Операции факторизации и поглощения дизъюнктов также являются неприменимыми к данному множеству дизъюнктов, поэтому переходим к шагу 4 алгоритма.

Граф связей, содержит дизъюнкты, поэтому переходим к шагу 1.

Выберем для резольвирования связь 8. После резольвирования по этой связи получаем дизъюнкт 9: ∅. Удаляем связь 8 и переходим к шагу 3 алгоритма.

Дизъюнкт 9 является пустым дизъюнктом, следовательно, исходное множество дизъюнктов является невыполнимым. Завершение работы алгоритма.

Доказана полнота и состоятельность процедуры вывода на графе связей. Вышеприведенный алгоритм является недетерминированным.

Для реализации его на детерминированной машине он нуждается в детерминированной процедуре выбора резольвируемой связи. В данном вопросе возможно использование нескольких основных методик, например, выбор связи, активация которой приведет к уменьшению количества дизъюнктов в графе, количества связей или количества вхождений предикатов в дизъюнкты. Идеальная ситуация возникает в случае, когда связь соединяет пару предикатов, не имеющих никаких других связей. Также к упрощению графа приводит слияние одинаковых предикатов из дизъюнктов-родителей. Еще одним фактором, влияющим на выбор связи, является единственность связи для предиката, что приводит, как сказано ранее, к удалению дизъюнкта, содержащего этот предикат после резольвирования. В случае, когда упрощения графа добиться не удается, следует выбрать связь, резольвирование которой приведет к минимальному усложнению графа связей. В этой ситуации следует отдавать предпочтение связям, резольвенты которых содержат наименьшее количество предикатов.

Выводы

Поскольку многие задачи могут быть сформулированы как задачи доказательства теорем, проблема автоматизации доказательств оказывается важной областью в искусственном интеллекте. Благодаря неустанным усилиям многих исследователей был достигнут большой прогресс в использовании машин для доказательства теорем.

Магистерская работа посвящена актуальной научной задаче разработки алгоритма логического вывода на графе связей. В рамках проведенных исследований выполнено:

  1. Выделены ключевые особенности метода резолюции на графе связей.
  2. Рассмотрена возможность создания оптимальной эвристики.
  3. Проведен ряд экспериментов по усовершенствованию представления графа связей для уменьшения ресурсоемкости алгоритма.

Дальнейшие исследования направлены на такие аспекты:

  1. Создание оптимальной эвристической функции для метода резолюции на графе связей.
  2. Разбиение графа связей на подграфы для уменьшения времени выполнения алгоритма.
  3. Разработка демонстрационной системы, реализующей предложенный в магистерской работе алгоритм метода резолюции.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2012 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Уайтхед А.Н. Основания математики: в 3 т. / Альфред Н. Уайтхед, Бертран Рассел; пер. с англ. Ю.Н. Радаева, И.С. Фролова; под ред. Г.П. Ярового, Ю.Н. Радаева. – Самара: Книга, 2005–2006. – 234 c.
  2. Alonzo Church, A Bibliography of Symbolic Logic, 1666–1935. – 164 pp.
  3. Alan M. Turing – Collected works of A. M. Turing. Mathematical logic. Elsevier, Amsterdam, The Netherlands, 2001. – 745 pp.
  4. Патнэм Х. Философия сознания / Пер. с англ. Л. Б. Макеевой, О. А. Назаровой, А. Л. Никифорова; предисл. Л. Б. Макеевой. М.: Дом интеллектуальной книги, 1999. 240 с.
  5. Патнэм Х. Разум, истина и история / Пер. с англ. Т.А. Дмитриева, М.В. Лебедева. – М.: Праксис, 2002. – 296 с.
  6. Патнэм Х. Как нельзя говорить о значении (комментарий к статье Дж. Дж. Смарта) // Структура и развитие науки. М., 1978. С. 396–418
  7. Патнэм Х. Значение и референция // Новое в зарубежной лингвистике. Вып. 13. М., 1982. С. 377–390.
  8. Робинсон А. Введение в теорию моделей и мета–математику алгебры. // Серия «Математическая логика и основания математики». М.: Наука, 1967, 378 с.
  9. Шанин Н.А. Алгорифм машинного поиска естественного логического вывода в исчислении высказываний // М.: Наука, 1965, 38 с.
  10. Лейбниц Г. В. Математические работы в переводе А. П. Юшкевича // Успехи Мат. Наук, – М.: Наука, 2003. – 235 с.
  11. Peano G. "The principles of arithmetic, presented by a new method" in Jean van Heijenoort, 1967. A Source Book in Mathematical Logic, 1879–1931. Harvard Univ. pp. 83–97.
  12. Генцен Г. Непротиворечивость чистой теории чисел. // Математическая теория логического вывода. М.: Наука, 1967, C. 77–153.
  13. Skolem, Th. (1934) Uber die Nicht–charakterisierbarkeit der Zahlenreihe mittels endlich oder abzahlbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen. Fundam. Math. 23, pp. 150–161.
  14. John W. Dawson, Jr. Logical Dilemmas: The Life and Work of Kurt Godel. AK Peters, Ltd., 1996. – 247 pp.
  15. Enderton H.B. A Mathematical Introduction to Logic // 2nd ed., Academic Press, 2001. 326 pp.
  16. Аверин А.И., Вагин В.Н. Параллелизм в дедуктивном выводе на графовых структурах,Автомат. и телемех., 2001, № 10. C. 54–64.
  17. Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фомина М.В. Достоверный и правдоподобный вывод в интеллектуальных системах Монография. Под ред. В.Н. Вагина и Д.А.Поспелова. М.: Изд. 2–ое исправл. и дополн. Физматлит, 2008, 714 с.
  18. Комендантский В.Е. Метод резолюций в смешанной логике Поста // Труды XVI научно–исследовательского семинара логического центраИФРАН. М.: ИФРАН, 2002. С. 64–74.
  19. Анисимов А.В., Вершинин К.П., Лялецкий А.В., Паскевич А.Ю. //Система автоматизации дедукции (САД) как средство обработки формальных компьютерных заданий . The Fourth International Conference Theoretical and Applied Aspects of Program Systems Development (TAAPSD’2007). Abstracts (4–9 September, 2007, Berdyansk, Ukraine), Київ, Р. 9–14.
  20. Богомолов А.М., Барашко А.С., Грунский И.С. Эксперименты с автоматами. – Киев: Наукова думка, 1973. – 144 с.
  21. Богомолов А.М., Грунский И.С., Сперанский Д.В. Контроль и преобразование дискретных автоматов. – Киев: Наукова думка, 1975. – 176 с.
  22. Грунский И.С., Козловский В.А. Синтез и идентификация автоматов. – Киев: Наукова думка, 2004. – 246 с.
  23. Волченко М.В. Представление термов для алгоритма резолюции логики высказываний. Информатики и компьютерные технологии / Материалы V международной конференции. – Донецк: Изд–во ДГТУ, 2009.
  24. Асеев И.И. – Алгебра степенных операторов [Электронный ресурс]. – Режим доступа: http://sceptic-ratio.narod.ru/ma.htm