Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- 3.1 Обзор международных источников
- 3.2 Обзор локальных источников
- 4. Топологические карты
- 5. Раскраска графа
- 5.1 Алгоритм распознавания графов тремя агентами
- 5.2 Востановление графов при помощи построения на его вершинах нумераций
- 6. Метод сравнения мобильным агентом своей среды и заданной карты
- Выводы
- Список источников
Введение
Основной проблемой теоретической кибернетики является проблема взаимодействия управляющей и управляемой систем (управляющего автомата и его операционной среды). Около истоков этой проблематики стояли В.М. Глушков и К. Шеннон. Взаимодействие автомату и среды чаще всего изображается как процесс передвижения автомата обозначенным графом или лабиринтом среды. Такое изображение интенсивно развивается в трудах В.Б. Кудрявцева и управляемой им школы. Автомат, находясь в вершине графа, воспринимает некоторую информацию об отметках локального около этой вершины, а также должен возможность изменять эти отметки и/или ставить дополнительные. На основании воспринятой информации автомат передвигается в некоторую смежную вершину [1].
Одной из центральных и актуальных как в теоретическом, так и прикладному аспектах проблем, которые возникают при исследовании взаимодействия автоматов и графов, есть проблема анализа или распознавания свойств графа при разной априорной информации и при разных способах взаимодействия автомата и графа.
Возник подход изучения проблемы навигации мобильных роботов. Этот подход основывается на том, что топологическая среда рассматривается как конечный неориентированный граф с помеченными концами ребер – вершинами графа.
1. Актуальность темы
В работах многих исследователей предложен ряд методов и алгоритмов решения таких задач: задачи самолокализации, то есть отличия некоторой вершины известного графа от всех других его вершин. Однако нет метода оптимального (или, по крайней мере, стремящегося к оптимальному, по определенным критериям) решения задачи самолокализации мобильного агента (робота) в топологической среде (графе). В конечном итоге эта проблема привлекла внимание исследователей к поиску оптимальных методов. В настоящий момент самолокализация мобильного робота в топологической среде стала неотъемлемой частью многих систем искусственного интеллекта. Данной проблемой начали заниматься сравнительно недавно. Следовательно, методов решения данной проблемы разработано немного, что и обуславливает отсутствие оптимальных методов решения поставленной задачи. Данная задача в последнее время приобрела значительную актуальность и практическую важность.
2. Цель и задачи исследования, планируемые результаты
Целью магистерской работы является разработка метода оптимального решения задачи сравнения карты с заранее известной средой при помощи мобильного агента (робота).
Основные задачи исследования:
- Изучить карту как среду движения агента.
- Рассмотреть примеры существующих топологических карт.
- Изучить основные определения и обозначения теории графов.
- Рассмотреть известные алгоритмы решения.
- Разработать метод сравнения карты и среды.
Объект исследования: контроль карты и среды агентом.
Предмет исследования: контроль неизвестной среды агентом с составлением на карте отметок пройденных вершин и ребер.
В рамках магистерской работы планируется получение актуальных научных результатов по следующим направлениям:
- Изучение и анализ существующих методов.
- Определить существующие виды графов, их обходы.
- Написать алгоритм сравнения карты и среды мобильным агентом, провести анализ полученного алгоритма с учетом затраченного времени на работу алгоритма и заполнения памяти данным алгоритмом.
3. Обзор исследований и разработок
Управляющая система, функционирующая в среде, является центральным понятием в кибернетике. Начало исследованиям таких систем положили работы В.М. Глушкова, А.А. Летичевского [2] и К. Шеннона [3] Взаимодействие управляющей системы и среды зачастую представляется как процесс перемещения управляющего автомата по графу (лабиринту) среды [6], что привело к возникновению обширной и интенсивно развивающейся области исследований поведения автоматов в лабиринтах [2,4,5] Констатирую высокий уровень развития исследований взаимодействия автомата и среды следует указать, что основное внимание уделяется проблеме анализа свойств управляющего автомата. В то же время не менее важна проблема анализа или распознавания графа, моделирующего операционную среду, длительное время оставалась в тени и сравнительно недавно стала привлекать внимание под влиянием прикладных задач мобильной связи и других. Для решения задачи анализа графа операционной среды требуется разработка средств и методов его описания, а также методов обработки таких описаний с целью получения заключений о свойствах и характеристиках графа. При решении проблемы анализа графа ОС наметились три основных подхода. Один из низ основании на том, что исследуемые графы рассматриваются как конечные автоматы без выхода (автоматные лабиринты), то есть как ориентированные графы с помеченными дугами [2–7]. Такой подход позволяет использовать методы и результаты теории автоматов: старейшей и наиболее развитой области теоретической кибернетики.
3.1 Обзор международных источников
Теоретическая кибернетика у ее истоков исследований стояли В.М. Глушков [2] и К. Шеннон [19]. Взаимодействие автомата и среды чаще всего представляется как процесс передвижения автомата обозначенным графом или лабиринтом среды. Такое представление интенсивно развивается в трудах В.Б. Кудрявцева и управляемой им школы [8–10]. При решении проблемы анализа графа операционной среды выделилось несколько подходов. Один из них основывается на том, что исследуемые графы рассматриваются как окончании инициальни автоматы без выхода. В рамках этого подхода в трудах Г.Ю. Кудрявцева [11], Р.М. Олейника [12,13] найдены точные верхние оценки наименьшего времени , за которое различаются два графа. В трудах Г. Дудека, М. Дженкина, Е. Милиоса и Д. Вилкеса [14–17] предложены методы и алгоритмы решения таких задач: задачи самой локализации, то есть отличая некоторой вершины известного графа от всех других его вершин, и задачи контроля карты, то есть отличая графа-эталона от заданного класса графов. В монографии Ю.В. Капитоновой и О.А. Летичевского [18] с вершинами таких графов естественно связанные языки в алфавите отметок и показано, что такие языки регулярны и не содержат пустое слово.
3.2 Обзор локальных источников
В Донецком национальном техническом университете (кафедра программное обеспечение интеллектуальных систем) решается проблема анализа графа операционной среды на основе чего и выделилось несколько подходов. Один из них основывается на том, что исследуемые графы рассматриваются как окончании инициальни автоматы без выхода, то есть как окончании ориентированы графы с обозначенными дугами. Такой подход позволяет использовать методы и результаты теории автоматов, которые являются наистаршими и наиболее развитой отраслью теоретической кибернетики. В рамках этого подхода в труде И.С. Грунского [12] найдены точные верхние оценки наименьшего времени, за которое различаются два графы, предложены методы и алгоритмы отличая графа-эталона от класса всех таких графов, в которых количество вершин не превышает количество вершин эталона. В роботе А.Н. Курганского [20] найден критерии при которых языки представимы в различного вида графах с помеченными вершинами, и построена иерархия таких языков.
4. Топологические карты
В контрасте к заранее обсуждаемым представлениям, которые большей частью сосредоточиваются на геометрической структуре окружения, топологические представления также получили существенный различие. В одном из руководств подходы к топологической картографии были представлены в 1988: эта была работа Куиперса и Бауна, пример на рисунке 4.1.
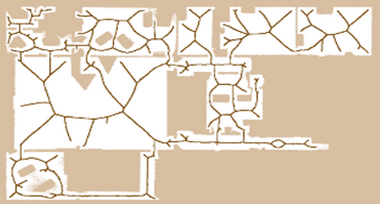
Рисунок 4.1 – Пример обобщенного графа Voronoi
В этом подходе, окружение представляется как подобная для графа структура, в которой узлы-locally различимые места, и узлы края путешествия, вдоль которых робот может двигаться между местами. Рисунок путешествия робота 4.2. Здесь, отличительные места идентифицированы по утверждению расстояние к соседним объектам. Отличительные места были определены как встречные пункты в обобщенных диаграммах Voronoi, то есть пункты со степенью три или больше. Обобщенная диаграмма Voronoi: это набор пунктов, равноудаленных от самого близкого до двух или больше границ препятствия.

Рисунок 4.2 – Пример движения мобильного робота между скал (препятствий)
Обобщенные диаграммы Voronoi это очень популярное представление, так как они могут рассматриваться как дорожные карты с высокой точностью к топологической структуре окружения. Они были окрашены энтенсивно для планирования пути. Чтобы планировать путь от стартовой позиции к конечному пункту в окружении, роботу придется сделать путь к обобщенному графу Voronoi, а затем от обобщенного Граф Voronoi к конечному пункту. Рисунок показывает пример обобщенного графа Voronoi для происходящего в движения робота. Отметим, что на данном рисунке только те части графа, которого может пересечь робот без сталкивания с объектами.
5. Раскраска графа
Раскрашивать можно как ребра графа, так и вершины. Коснемся сначала задачи о раскраске вершин, при этом считаем, что граф не ориентирован и не является мультиграфом
Задача. Раскрасить вершины графа так, чтобы любые две смежные вершины были раскрашены в разные цветы, при этом число использованных цветов должно быть наименьшим. Это число называется хроматическим (цветным) числом графа, будем его обозначать a= a (G) (если G – данный граф). Если число k і a , то граф называется k-раскрашиваемым.
Функцией Гранди называется функция на вершинах графа, отображаю-щая вершины в множество {1,2,…, a}, причем если вершина xi окрашена в цвет с номером k, то функция Гранди h(xi) = k.
Ясно, что для данного графа хроматическое число является единствен-ным, но функций Гранди может быть очень много. Естественно, что найти хотя бы одну функцию Гранди – это значит, найти одну из возможных “наилучших” раскрасок (таких раскрасок может быть много).
Заметим, что если данный граф является полным, т. е. любые две вершины являются смежными, то хроматическое число такого графа равно п, где n – число вершин.
Для дальнейшего понадобится следующее определение.
Набор вершин графа называется максимальной независимой системой (МНС), если любые две вершины из этого набора не являются смежными и нельзя включить в этот набор другую вершину, чтобы это условие сохранилось. Заметим, что нахождение МНС в графе достаточно просто: берем произволную вершину, затем находим любую вершину, не смежную с ней, затем находим вершину, не смежную с отобранными вершинами и т. д. Естественно, что МНС в данном графе может быть много и они могут содержать разное число вершин. Перейдем к описанию алгоритма нахождения наилучшей раскраски вершин графа. Пусть имеем граф G, найдем в нем какую-либо МНС, которую обозначим S1, и все вершины, входящие в эту МНС, окрасим в цвет № 1. Далее, удалим из данного графа все вершины, входящие в эту МНС (вместе с ребраребрами), и для нового графа снова найдем МНС, которую обозначим S2. Эти новые вершины окрасим в цвет № 2, затем удалим эти вершины из графа вместе с соответствующими ребрами и снова находим МНС, которую окрасим в цвет № 3, и т. д. Можно доказать, что при любом способе осуществления этой процедуры придем к наилучшей раскраске и найдем некоторую функцию Гранди и хроматическое число данного графа [6].
Пример. У графа (см. рис. 5.1) имеется 3 максимально независимых систем вершин: {5}, {1,3} и {2,4}. Ясно, что при любой процедуре нахождения хроматического числа в этом графе, получим число 3.
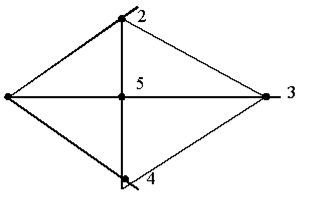
Рисунок 5.1 – Пример графа
Теорема. Если максимальная степень вершин в графе равна r, то хроматическое число этого графа не превосходит r + 1. При этом хроматическое число графа равно r + 1 только в двух случаях: во-первых, если граф является полным и, во-вторых, если r = 2 и при этом данный граф содержит контур нечетной длины (такой граф изображен на рис. 5.2, максимальная степень его вершин – 2, а хроматическое число – 3). Во всех остальных случаях хроматическое число графа не превосходит максимальной степени вершин.
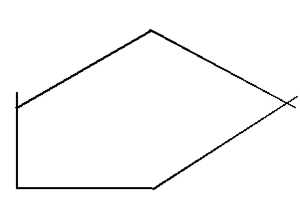
Рисунок 5.2 – Пример графа содержащий контур нечетной длины
Примечание. Оценка хроматического числа, даваемого этой теоремой, является достаточно грубой. Особенно наглядно это выглядит на примере дерева для которого степень вершин может быть как угодно велика, а хроматическое число равно 2.
Рассматриваемые вопросы связаны с известной проблемой четырех красок. Для того чтобы ее сформулировать, нам понадобятся еще несколько определений.
Граф называется плоским, если он нарисован на плоскости, причем любые 2 ребра могут пересекаться только в вершине.
Графы называются изоморфными, если существует такая нумерация вершин в этих графах, что они имеют одну и ту же матрицу смежности (фактически изоморфные графы – это одинаковые графы, которые отличаются только другим изображением) [21].
Граф называется планарным, если он изоморфен плоскому графу. Таким образом, планарный граф можно изобразить на плоскости как плоский.
Можно доказать (это не совсем простая теорема), что хроматическое число планарных графов меньше или равно 5. Однако Августом де Морганом (1850) была выдвинута гипотеза о том, что хроматическое число планарных графов меньше или равно 4. Этой проблеме было посвящено огромное число математических работ. В конце концов, удалось свести эту проблему к исследованию верности этой гипотезы для достаточно большого числа типов графов (около 30 тыс.), что и было сделано с помощью компьютеров (1976). Гипотеза о четырех красках оказалась справедливой, а сама проблема перешла в задачу об упрощении доказательства гипотезы о четырех красках.
Отметим самую известную интерпретацию проблемы о четырех красках. Пусть имеется географическая карта. Можно ли, используя только 4 краски, изобразить эту карту так, чтобы соседние страны (имеющие общую границу) были окрашены в разный цвет. Понятно, что в соответствующем графе вершинами являются страны, а смежными вершинами являются соседние страны. Ясно, что полученный граф является планарным, и после 1976 г. ответ на этот вопрос является положительным [21].
Заметим, что в теории графов ставится часто вопрос о реберной раскраске графов. Какое минимальное число цветов (это число иногда называют реберно-хроматическим) нужно, чтобы раскрасить ребра графа так, что любые 2 смежных ребра (т. е. 2 ребра, имеющих общую вершину) были бы окрашены в разный цвет Для реберно-хроматического числа графа справедлива гораздо более точная оценка, чем для просто хроматического числа, а именно, верна следующая, в какой-то степени удивительная, теорема.
Теорема Визинга. Если в графе максимальная степень вершин равна r, то реберно-хроматическое число равно либо r, либо r +1.
Заметим, что до сих пор нет «хороших» критериев для графов, когда же именно реберно-хроматическое число равно r, а когда r + 1 [22].
Очевидно, что простейший алгоритм нахождения реберно-хроматического числа (и соответствующей раскраски ребер) состоит в следующем: по данному графу строим так называемый двойственный граф: ребра графа соответствуют вершинам нового (двойственного) графа, причем, если 2 ребра имеют общую вершину, то они являются смежными и в двойственном графе соединены ребром. После этого раскрашиваем наилучшим образом вершины двойственного графа и, переходя к «старому» графу, получаем (одну из возможных) наилучших реберных раскрасок графов [24].
5.1 Алгоритм распознавания графов тремя агентами
Рассматриваемый алгоритм основан на стратегии поиска в глубину.
Эта стратегия такова: агенты идут «в глубину», пока это возможно, возвращаются назад, ищут другой путь с еще не посещенными вершинами и не пройденными ребрами. В случае обнаружения смежной вершины, окрашенной в «чужой» цвет, агент метит все перешейки из текущей вершины в чужую область и сообщает второму АИ, через агента-экспериментатора, о необходимости распознавания помеченных перешейков. Пока второй АИ распознает перешейки, первый АИ не может метить новые перешейки. В случае отсутствия других возможных вариантов перемещения, кроме как пометить новый перешеек, первый АИ останавливается до того момента, пока второй АИ не распознает все помеченные перешейки.
Предлагаемая стратегия обладает рядом особенностей:
1) граф G агентам не известен;
2) при обходе графа G , агенты создают неявную нумерацию пройденных вершин: при первом посещении вершины она окрашивается агентом A в красный цвет (в желтый цвет в случае агента B) и ей фактически ставится в соответствие номер, равный значению переменной Сч_А для агента A (Сч_B для агента B ).
Отметим, что Сч_А и Сч_B принимают соответственно нечетные и четные значения. На основе нумерации и происходит восстановление графа путем построения графа H изоморфного G. В процессе обхода агенты строят неявные деревья поиска в глубину. Относительно этих деревьев все ребра разделяются на древесные (окрашиваются при первом прохождении по ним красным либо желтым цветом), обратные (не принадлежат дереву и окрашиваются при первом прохождении в черный цвет) и ребра перешейки (соединяют деревья, построенные разными агентами). Древесные ребра проходятся как минимум 2 раза и при последнем проходе окрашиваются агентами в черный цвет. Обратные ребра проходятся один раз. А вот ребра перешейки проходятся каждым агентом по два раза: первый прошедший по нему агент метит перешеек, окрашивая его в красный цвет в случае агента A (в желтый цвет в случае агента B ), второй прошедший по нему агент распознает перешеек и красит его в черный цвет [25].
Красные (желтые) вершины графа G , на каждом шаге алгоритма, образуют красный (желтый) если это не возврат для распознания перешейков) – укорачивается, при распознавании обратного ребра и перешейков – не изменяется. Вершина, у которой все инцидентные ребра распознаны, окрашивается в черный цвет. Алгоритм заканчивает работу, когда красный и желтый пути становятся пустыми, а все вершины черными [23].
Обход графа. В работе АИ можно выделить 5 режимов:
I. Обычный режим. АИ движется вперед по белым вершинам, окрашивая вершины, соединяющие их ребра и дальние инциденторы в «свой» цвет. Если нет возможных путей перемещения, то АИ возвращается назад, окрашивая пройденные вершины, ребра и ближние инциденторы в черный цвет. Вернувшись в начальную вершину, АИ завершает работу. На каждом шаге АИ обменивается данными с АЭ [24].
II. Распознавание обратных ребер. Если при движении вперед было обнаружено обратное ребро, то агент прекращает работу в обычном режиме. АИ переходит по обратному ребру, окрашивая его в черный цвет, и по своему пути возвращается в вершину, в которой сменил режим работы. Достигнув этой вершины, агент переключается в обычный режим работы. На каждом шаге АИ обменивается данными с АЭ [24].
III. Пометка перешейков. Если в процессе обхода графа был обнаружен перешеек, то при условии, что все ранее помеченные данным АИ перешейки были распознаны, агент переключается в режим пометки перешейков. В этом режиме АИ переходит по перешейку в чужую область, окрашивая ребро и дальний инцидентор в «свой» цвет. На следующем шаге возвращается по этому перешейку, ничего не окрашивая, и ищет другие перешейки из этой вершины. Пометив все перешейки, АИ сообщает об этом АЭ, который в свою очередь, дает команду второму АИ о необходимости распознавания помеченных перешейков. По завершению режима пометки перешейков АЭ содержит информацию о количестве помеченных перешейков [24].
VI. Распознавание перешейков. Получив от АЭ команду о необходимости распознавания перешейков, АИ переключается в режим распознавания перешейков. Если в этот момент агент работает в режиме распознавания обратного ребра, то АИ переключится в режим распознавания перешейков, лишь по завершению распознавания обратного ребра. В этом режиме АИ возвращается назад по своему пути до обнаружения ближайшей вершины, инцидентной помеченному перешейку. Под помеченным перешей ком понимается ребро, у которого ближний инцидентор, ребро и дальняя вершина этого ребра окрашены в «чужой» цвет. Далее возможны два случая: Помечено один перешеек. АИ переходит по нему в чужую область, окрашивая перешеек в «свой» цвет, а дальний инцидентор в черный. На следующем шаге возвращается по этому перешейку в свою область, окрашивая дальний инцидентор и перешеек в черный цвет. Далее движется вперед по своему пути, пока не вернется в вершину, в которой было произведено переключение в режим распознавания перешейков. Помечено не менее двух перешейков. АИ переходит по первому найденному помеченному перешейку в чужую область, окрашивая его в «свой» цвет, а дальний инцидентор в черный. На следующем шаге АИ возвращается по этому перешейку в свою область, окрашивая его в черный цвет, а оба инцидентора в красный. Далее АИ движется назад по своему пути, пока не будет найден следующий помеченный перешеек. Далее возможно два варианта [23].
1. Следующий помеченный перешеек не последний. АИ переходит по найденному перешейку, окрашивая его в «свой» цвет, а дальний инцидентор в черный. На следующем шаге АИ возвращается поэтому перешейку в свою область, окрашивая его и оба инцидентора в черный цвет. И снова возвращается назад по своему пути до следующего помеченного перешейка.
2. Следующий помеченный перешеек последний. АИ переходит по най-денному перешейку, окрашивая его в «свой» цвет, а дальний инцидентор в черный. На следующем шаге АИ возвращается по этому перешейку в свою область, окрашивая его в черный цвет, а оба инцидентора в красный. АИ переходит по последнему перешейку в чужую область, окрашивая инциденторы в черный цвет. На следующем шаге АИ переходит по первому распознанному перешейку в свою область, окрашивая инциденторы в черный цвет. Далее АИ возвращается в вершину, в которой было произведено переключение в режим распознания перешейков.
V. Одновременное попадание двух АИ в одну белую вершину. При одновременном попадании двух АИ в одну белую вершину, каждый АИ окрашивает вершину наполовину, и она становится красно-желтой. Агент B на следующем шаге отступает назад по своему пути и переходит в режим пометки перешейков (при этом ребро, по которому он вернулся уже посчитано как первый перешеек, а длина желтого пути уменьшена на одну вершину). Агент A видит разноцветную вершину как свою, но при распознавании окрашивает в черный цвет обе половинки.
5.2 Восстановление графов при помощи построения на его вершинах нумерации
Задан граф G связный, конечный, неориентированный, без петель и ратных ребер, элементы которого можно метить специальными красками. Задан агент, который может передвигаться по графу из вершины в вершину, по ребру, соединяющему их, «видеть» (воспринимать) и анализировать локальную информацию об 1-окрестности вершины, в которой он находится, выбирать направление движения и способ покраски элементов на основе полученной информации об 1-окрестности вершины. Изначально предполагается, что агент помещается в произвольную вершину графа G, а все его элементы помечены.
Требуется разработать такой метод обхода графа G и раскраски его элементов, чтобы агент по полученной информации об 1-окрестностях вершин смог построить граф H изоморфный графу G с точностью до меток на элементах графов.
Рассмотрим поставленные задачи:
1) построение базового метода восстановления графа основанного на по-строении нумерации на его вершинах и построение на основе этого метода полиномиального базового алгоритма;
2) исследование временной емкостной сложности базового алгоритма, а также количество различных видов красок используемых агентом для восстановления графа;
3) анализ базового алгоритма выделение основных этапов, нахождение модификаций на которых достигаются лучшие верхние оценки временной емкостной сложности;
4) нахождение классов графов и операций над ними, которые не ухудшают верхнюю оценку временной сложности выполнения базового метода или его модификаций.
Идея базового метода. Обойти граф «в глубину», строя при этом неявную нумерацию на вершинах графа G, и неявное дерево поиска в глубину, отмечая вершины, ребра и инциденторы красной краской и разбивая тем самым множество ребер графа на два множества: древесные и обратные. При помощи неявной нумерации восстанавливать и метить черной краской обратные ребра при первом их появлении в вершине, в которой находиться агент, а древесные при первом прохождении по ним. Не явность нумерации заключается в том, что явно номер не ставится на вершину или другой элемент графа, а вычисляется на основе меток на элементах графов.
Основные этапы «Базового алгоритма» [24]:
1. Инициализация.
2. Процедура ВПЕРЕД. Поиск раннее не пройденного белого ребра и переход по нему.
3. Процедура НАЗАД. Завершение полного исследования вершины, переход по красному ребру, по которому агент впервые попал в данную вершину, пометка вершины и этого ребра черной краской.
4. Процедура ВОССТАНОВЛЕНИЯ. Восстановление обратного ребра на основе неявной нумерации вершин графа и его пометка черной краской.
5. Остановка алгоритма после восстановления всех вершин, древесных и обратных ребер графа.
Модификации базового алгоритма алгоритма.
Модификация 1. Агент, который проводит эксперимент по восстановлению графа, может быть разделен на два агента: агент исследователь (АИ) и агент экспериментатор (АЭ). Первый перемещается по восстанавливаемому графу, собирает информацию о метках на элементах графа, передает о своих перемещениях и изменениях меток на элементах графа АЭ. АЭ по сообщениям АИ строит представление восстанавливаемого графа в своей внутренней памяти;
Модификация 2. Агент в отличии от базового метода восстанавливает все обратные ребра каждой вершины;
Модификация 3. Агент восстанавливает обратные ребра не при первом их появлении, а при попадании агента в вершину из которой он может попасть только в ранее посещенные;
Модификация 4. Все вершины графа разбиваются на два множества: ординарные и не ординарные. Ординарные – вершины, валентность которых не более чем D, где D – заранее известная константа. В противном случае вершина не ординарная. Предполагается, что две неординарные вершины не смежных между собой;
Модификация 5. Агент реализует неявную нумерацию при помощи камней со счетчиками, которые после восстановления всех обратных ребер можно использовать повторно.
Предложен базовый метод восстановления ранее неизвестного графа с точностью до меток на элементах графов, при помощи передвигающегося по нему агента. На основе метода построен «Базовый алгоритм», который использует две краски и имеет временную сложность T(G), O(n)<=T(G)<=O(n3) [25].
Найдены операции над графами такие, что результирующий граф имеет верхнюю оценку временной сложности, не хуже, чем исходные.
Базовый метод допускает модификации, которые позволяют получить лучшую оценку временной сложности и упрощают агента, который передвигается по графу, однако, накладывают дополнительные ограничения на восстанавливаемый граф [25].
Модификация 1 – мобильный агент, O(n)<=T(G)<=O(n3).
Модификация 2 – O(n) <= T(G) <= O(n2).
Модификация 3 – порождает новые алгоритмы восстановления графа, но не улучшает сложность алгоритмов.
Модификация 4 – агент конечный автомат, классы графов для которых T(G)=O(n) , S(G) = O(n).
Модификация 5 – T(G)=O(n), агент использует две краски и ht камней, где ht – наибольшая высота дерева при обходе графа в глубину.
6. Метод сравнения мобильным агентом своей среды и заданной карты
Вход:
неориентированные связные графы G1 и G2
,
вершины и ребра которых не отмечены (отмечены белой краской).
Выход:
сообщение графы изоморфны или
нет.
Метод:
параллельное движение в G1 и G2 по неотмеченным или зеленым ребрам через
неотмеченные или красные вершины до тех пор, пока есть хоть одна не
черная
вершина в графе. При этом пройденные вершины и ребра окрашиваются в
соответствии с алгоритмом.
1.
Агент
начинает анализ вершины v;
2.
Если
вершине v инцидентно
несколько ребер, то агент
ставит в v флажок
красного цвета и идет в новую
смежную вершину, окрашивая ребро между
вершинами зеленым цветом;
3.
Агент
на карте G2 помечает
вершины и пройденные им ребра
тем же цветами и флажками, что и на среде G2;
4.
Агент
сравнивает пройденные вершины и ребра в карте G2
с
пройденными вершинами и ребрами в среде G1,
5.
Если исследуемый участок карты G2
совпадает с исследованным участком
среды G1 и на
карте есть не пройденные вершины и
ребра, то переходит в 1;
6.
Если
исследуемый участок карты G2
совпадает с
исследованным участком среды G1 и
больше нет не
пройденных вершин и ребер, то карта G2
изоморфна G1
переходит к 10;
7.
Иначе
G1 не
изоморфен G2
переходит
к 10;
8. Если число
ребер q,
инцидентных вершине v,
равно 1, то ставится флажок черного цвета и агент следует в смежную ей
вершину,
окрашивая ребро зеленым цветом:
8.1 Если
смежная
вершина имеет черный флажок, то переходит к 3, а затем к 5;
8.2 Иначе
переходит
к 3, а затем к 5;
9.
Если
число ребер q,
инцидентных вершине v
равно 2, то рассматривается такая ситуация
9.1 Если
в вершине v среды
G1
существует
инцидентное ей зеленое ребро и на одной из смежных ей вершин стоит
черный
флажок, то агент ставит на вершине v черный
флажок и переходит в смежную вершину
(отмеченную белой краской, либо красным флажком), где нет черного
флажка;
9.2 Переходит
к 3–4;
9.3 Если
в вершине v среды
G1
все
инцидентные ей ребра зеленые и на обеих
смежных вершинах стоят черные флажки, то в вершине v агент
ставит
черный флажок;
9.4
Переходит к 3,
а затем к 6;
9.5 Если
в вершине v среды
G1
все
инцидентные ей ребра белые, то
выбирается
смежная вершина, на которой стоит красный флажок;
9.6 Иначе
выбирает
смежную белую вершину и переходит к 1;
9.7 Если
смежная вершина вершине v c
черным флажком, то переход к 6.
10.
Конец
алгоритма.
Работа алгоритма представлена на рисунке 6.1
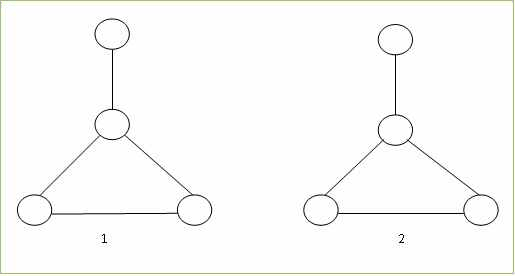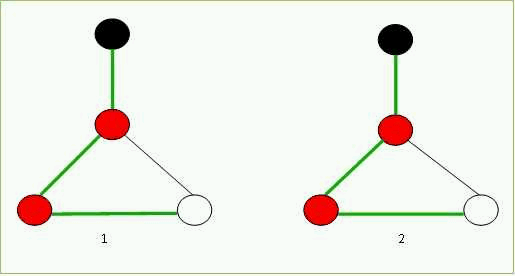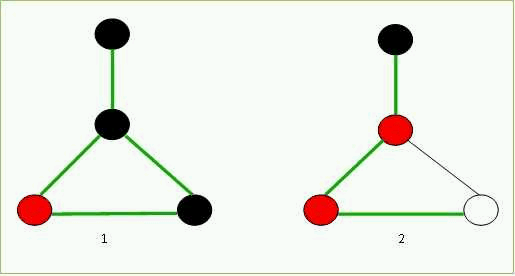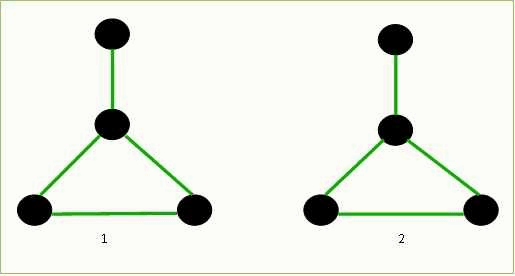
Рисунок 6.1 – Алгоритм сравнения мобильным агентом своей среды и заданной карты
(анимация: 6 кадров, 3 циклов повторения, 99 килобайта)
(1 – среда изучения агента, 2 – карта агента)
Выводы
В процессе выполнения данной работы были решены следующие задачи:
1) изучена карта как среда движения агента;
2) рассмотрены примеры существующих топологических карт;
3) рассмотрены известные алгоритмы решения;
4) разработан метод сравнения карты и среды;
5) произведен ручной просчет метода.
В последующем, результаты будут использоваться для написания дипломного проекта, в котором предполагается:
1) разработать программную реализацию описанного метода;
2) провести анализ полученных результатов и корректность полученных алгоритмов.
Список источников
- Сапунов С. В. Диссертация на соискание научной степени кандидата физико-математических наук: Анализ графов с помеченными вершинами / Сапунов С. В. – Донецк, 2007. – 180 с.
- Кудрявцев В. Б. Введение в теорию автоматов / Кудрявцев В. Б. – М. : Наука, 1985. – 320 с.
- Глушков В. М. Теория дискретных преобразователей / Глушков В. М. – Новосибирск: Наука, 1973. – 100 с.
- Кирильченко А. А. Теоретические аспекты организации интерпрети-рующей навигации мобильного робота / Кирильченко А. А. – М., 2002. – 37 с.
- Емеличев В. А. Лекции по теории графов / Емеличев В. А. – М. : Наука, 1990. – 384 с.
- Dudek G. Map validation and Robot Self-Location in a Graph-Like World / Dudek G // Robotics and Autonomous Systems. – 1997. – Vol. 22, №2. – P. 159–178.
- Макконелл Д. Анализ алгоритмов. Вводный курс / Макконелл Д. – М. : Техносфера, 2002. – 304 с.
- Килибарда Г. Независимые системы автоматов в лабиринтах. Дискретная математика / Килибарда Г. – М. : Наука, 2003. – Т. 15, вып. 2, – 139 с.
- Килибарда Г., Кудрявцев В.Б., Ушчумличь Щ. Коллективы автоматов в лабиринтах // Дискретная математика. – 2003. – Т. 15, вып. 3. – С. 3–40.
- Кудрявцев В.Б., Ушчумличь Щ. О поведении автоматов в лабиринтах // Дискретная математика. – 1992. – Т. 4, вып. 3. – С. 3–28.
- Кудрявцев Г.Ю., О длине тестовых автоматов реализуемых эксперементов с автоматными лабиринтами // Дискретная математика. – 1992. – Т. 4, вып. 3. – С. 86–100.
- Грунский И.С., Олейник Р.И. Об отличимости инициальных лабиринтов конечными автоматами // Интеллектуальные системы. – 1999. – Т. 4, вып. 3–2. – С.243–272.
- Олейник Р.И. О контроле автоматных лабиринтов конечным автоматом // Труды ИМПММ НАНУ. – 2000. – Т. 5. – С. 107–114.
- Dudek G. Robotik exploration as graph construction / Dudek G // IEEE Transactions on on Robotics and Automation. – 1991. – Vol. 7, №6. – P, 859–864.
- Dudek G. Map validation in a graphlike world / Dudek G // Proceedings of the 13th International Joint Conference on Artifical Intelligence (Chamdery, France, August 1993). – San Fransisco: Morgan Kaufmann Publishers Inc., 1993. – P. 1648–1653.
- Dudek G. Map validation and Robot Self-Location in a Graph-Like World / Dudek G // Robotics and Autonomous Systems. – 1997. – Vol. 22, №2. – P. 159–178.
- Dudek G., Jenkin M. Computational Principles of Mobile Robotics. / Dudek G., Jenkin M. // Robotics and Autonomous Systems. – 2000. – Cambridg. – P. 159–178.
- Капитанова Ю. В. Математическая теория проектирования вычислительных систем / Капитанова Ю. В. – М. : Наука, 1988. – 296 с.
- Shannon Cl.E. Presentation of a maze-solving machine // Cybernetics: Circular, Circular and Feedback Mechanisms in Biological and Social System: Transactions of VIII Conference (Mfrch 15–16, 1951). – New York: Josian Macy Jr. Foubdation, 1952, – P. 169–181.
- Грунский И.С., Курганский А.Н. Языки грыфов с помеченными вершинами // Труды ИМПММ НАНУ. – 2004. – Т. 9. – С. 53–60.
- Макконелл Д. Анализ алгоритмов. Вводный курс / Макконелл Д. – М. : Техносфера, 2002. – 304 с.
- Москинова Г.И. Дискретная математика. / Москинова Г. И. – М. : Логос, 2000. – 198 с.
- Будах Л. Лабиринты и автоматы. Проблемы кибернетики / Будах Л. – М.: Наука, 1978. – 94 с.
- Грунский И. С. Свойства языков, порождаемых неориентированными графами с отмеченными вершинами / Грунский И.С. // Материалы VIII Международного семинара «Дискретная математика и ее приложения» (2–6 февраля 2004 г.) – М. : Изд-во мех.-мат. ф-та МГУ, 2004. – С. 259–269.
- Емеличев В. А. Лекции по теории графов / Емеличев В. А. – М. : Наука, 1990. – 384 с.
