Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд локальних джерел
- 4. Топологічні карти
- 5. Розфарбовування графа
- 5.1 Алгоритм розпізнавання графів трьома агентами
- 5.2 Востановленіє графів за допомогою побудови на його вершинах нумерацій
- 6. Метод порівняння мобільним агентом свого середовища і заданої карти
- Висновки
- Перелік посилань
Втуп
Основною проблемою теоретичної кібернетики є проблема взаємодії систем, що управляють і керованої (автомата, що управляє, і його операційного середовища). Біля витоків цієї проблематики стояли В.М. Глушков і К. Шенон. Взаємодія автомату і середовища найчастіше зображається як процес пересування автомата позначеним графом або лабіринтом середовища. Таке зображення інтенсивно розвивається в працях В.Б. Кудрявцева і керованої ним школи. Автомат, знаходячись у вершині графа, сприймає деяку інформацію про відмітки локального біля цієї вершини, а також повинен можливість змінювати ці відмітки і ставити додаткові. На підставі сприйнятої інформації автомат пересувається в деяку суміжну вершину [1].
Одній з центральних і актуальних як в теоретичному, так і прикладному аспектах проблем, які виникають при дослідженні взаємодії автоматів і графів, є проблема аналізу або розпізнавання властивостей графа при різній апріорній інформації і при різних способах взаємодії автомата і графа.
Виник підхід вивчення проблеми навігації мобільних роботів. Цей підхід грунтується на тому, що топологічне середовище розглядається як кінцевий неорієнтований граф з поміченими кінцями ребер – вершинами графа.
1. Актуальність теми
У роботах багатьох дослідників запропонований ряд методів і алгоритмів вирішення таких завдань: завдання самолокалізациі, тобто відмінності деякої вершини відомого графа від всіх інших його вершин. Проте немає методу оптимального (або, принаймні, прагнучого до оптимального, по певних критеріях) рішення задачі самолокалізациі мобільного агента (робота) в топологічному середовищі (графі). Зрештою ця проблема привернула увагу дослідників до пошуку оптимальних методів. Зараз самолокалізация мобільного робота в топологічному середовищі стала невід'ємною частиною багатьох систем штучного інтелекту. Даною проблемою почали займатися порівняно недавно. Отже, методів вирішення даної проблеми розроблені небагато, що і обуславліваєт відсутність оптимальних методів рішення поставленої задачі. Дане завдання останнім часом придбало значну актуальність і практичну важливість.
2. Мета і задачі дослідження та заплановані результати
Метою магістерської роботи є розробка методу оптимального рішення задачі порівняння карти із заздалегідь відомим середовищем за допомогою мобільного агента (робота).
Основні задачі дослідження:
- Вивчити карту як середовище руху агента.
- Розглянути приклади існуючих топологічних карт.
- Вивчити основні визначення і позначення теорії графів.
- Розглянути відомі алгоритми рішення.
- Розробити метод порівняння карти і середовища.
Об'єкт дослідження: контроль карти і середовища агентом.
Предмет дослідження: контроль невідомого середовища агентом із складанням на карті відміток пройденних вершин і ребер.
В рамках магістерської роботи планується отримання актуальних наукових результатів по наступним напрямкам:
- Вивчення і аналіз існуючих методів.
- Визначити існуючі види графів, їх обходи.
- Написати алгоритм порівняння карти і середовища мобільним агентом, провести аналіз отриманого алгоритму з врахуванням витраченого часу на роботу алгоритму і заповнення памʼяті даним алгоритмом.
3. Огляд досліджень та розробок
Система, що управляє, функціонує в середовищі, є центральним поняттям в кібернетиці. Почало дослідженням таких систем поклали роботи В.М. Глушкова, А.А. Летічевського [2] і К. Шеннона [3]. Взаємодія системи, що управляє, і середовища частенько представляється як процес переміщення автомата, що управляє, по графові (лабіринту) середовища [6], що привело до виникнення обширної області досліджень поведінки автоматів, що інтенсивно розвивається, в лабіринтах [2,4,5] Констатую високий рівень розвитку досліджень взаємодії автомата і середовища слід вказати, що основна увага приділяється проблемі аналізу властивостей автомата, що управляє. В той же час не менш важлива проблема аналізу або розпізнавання графа, що моделює операційне середовище, тривалий час залишалася в тіні і порівняно недавно стала привертати увагу під впливом прикладних завдань мобільного звʼязку і інших. Для вирішення завдання аналізу графа операційного середовища потрібна розробка засобів і методів його опису, а також методів обробки таких описів з метою здобуття висновків про властивості і характеристики графа. При вирішенні проблеми аналізу графа ОС намітилися три основні підходи. Один з низ підставі на тому, що досліджувані графи розглядаються як кінцеві автомати без виходу (автоматні лабіринти),тобто як орієнтовані графи з поміченими дугами [2–7]. Такий підхід дозволяє використовувати методи і результати теорії автоматів: старою і найбільш розвиненої області теоретичної кібернетики.
3.1 Огляд міжнародних джерел
Теоретична кібернетика в її витоків досліджень стояли В.М. Глушков [2] і К. Шеннон [19]. Взаємодія автомата і середовища найчастіше представляється як процес пересування автомата позначеним графом або лабіринтом середовища. Така вистава інтенсивно розвивається в працях В.Б. Кудрявцева і керованої ним школи [8–10] При вирішенні проблеми аналізу графа операційного середовища виділилося декілька підходів. Один з них грунтується на тому, що досліджувані графи розглядаються як закінченні ініциальні автомати без виходу. В рамках цього підходу в працях Г.Ю. Кудрявцева [11], Р.М. Олейника [12,13] знайдені точні верхні оцінки найменшого часу, за який розрізняються два графи. У працях Р. Дудека, М. Дженкина, Е. Міліоса і Д. Вілкеса [14–17] запропоновані методи і алгоритми вирішення таких завдань: завдання самої локалізації, тобто відрізняючи деякої вершини відомого графа від всіх інших його вершин, і завдання контролю карти, тобто відрізняючи графа-еталону від заданого класу графів. У монографії Ю.В. Капітонової і О.А. Летічевського [18]. з вершинами таких графів природно зв’язані язики в алфавіті відміток і показано, що такі мови регулярні і не містять порожнє слово.
3.2 Огляд локальних джерел
У Донецькому національному технічному університеті (кафедра програмне забезпечення інтелектуальних систем) вирішується проблема аналізу графа операційного середовища на основі чого і виділилося декілька підходів. Один з них грунтується на тому, що досліджувані графи розглядаються як закінченні ініциальні автомати без виходу, тобто як закінченні орієнтовані графи з позначеними дугами. Такий підхід дозволяє використовувати методи і результати теорії автоматів, які є наїстаршимі і найбільш розвиненою галуззю теоретичної кібернетики. В рамках цього підходу в праці І.С. Грунського [12] знайдені точні верхні оцінки найменшого часу, за який розрізняються дві графи, запропоновані методи і алгоритми відрізняючи графа-еталону від класу всіх таких графів, в яких кількість вершин не перевищує кількість вершин еталону. У роботові А.Н. Курганного [12] знайдений критерії при яких мови представіми в різного вигляду графах з поміченими вершинами, і побудована ієрархія таких мов.
4. Топологічні карти
У контрасті до заздалегідь обговорюваних вистав, які переважно зосереджуються на геометричній структурі оточення, топологічні вистави також отримали істотний відмінність. У одному з керівництва підходи до топологічної картографії були представлені в 1988: ця була робота Куїперса і Бауна, приклад на малюнку 4.1.
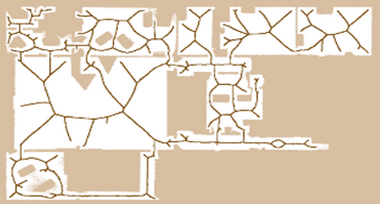
Малюнок 4.1 – Приклад узагальненого графа Voronoi
У цьому підході, оточення представляється як подібна для графа структура, в якій узли-locally помітні місця, і вузли краю подорожі, уздовж яких робот може рухатися між місцями приклад на малюнку 4.2. Тут, відмітні місця ідентифіковані за твердженням відстань до сусідніх обʼєктів. Відмітні місця були визначені як зустрічні пункти в узагальнених діаграмах Voronoi, тобто пункти з мірою три або більше. Узагальнена діаграма Voronoi: це набір пунктів, рівновіддалених від найближчого до двох або більше кордонів перешкоди.

Малюнок 4.2 – Приклад руху мобільного робота між скель (перешкод)
Узагальнені діаграми Voronoi це дуже популярна вистава, оскільки вони можуть розглядатися як дорожні карти з високою точністю до топологічної структури оточення. Вони були забарвлені ентенсивно для планерування дороги. Щоб планувати дорогу від стартової позиції до кінцевого пункту в оточенні, роботові доведеться зробити дорогу до узагальненого графа Voronoi, а потім від узагальненого Граф Voronoi до кінцевого пункту. Малюнок показує приклад узагальненого графа Voronoi для робота, що відбувається в рухи. Відзначимо, що на даному малюнку лише ті частини графа, якого може пересікти робот без зіштовхування з об'єктами.
5. Розфарбовування графа
Розфарбовувати можна як ребра графа, так і вершини. Торкнемося спочатку завдання про розфарбовування вершин, при цьому вважаємо, що граф не орієнтований і не є мультиграфом.
Завдання. Розфарбувати вершини графа так, щоб будь-які дві суміжні вершини були розфарбовані в різні квіти, при цьому число використаних кольорів має бути найменшим. Це число називається хроматичним (кольоровим) числом графа, його позначатимемо a= а (G) (якщо G – даний граф). Якщо число до і а, те граф називається дорозфарбовуваним.
Функцією Гранді називається функція на вершинах графа, що відображує вершини в безліч {1,2., а}, причому якщо вершина xi забарвлена в колір з номером до, то функція Гранді h(xi)= k.
Ясно, що для даного графа хроматичне число є єдиним, але функцій Гранді може бути дуже багато. Природно, що знайти хоч би одну функцію Гранді – це означає, знайти одне з можливих “найкращих” розфарбовувань (таких розфарбовувань може бути багато).
Відмітимо, що якщо даний граф є повним, тобто будь-які дві вершини є суміжними, то хроматичне число такого графа рівне n, де n – число вершин.
Для подальшого знадобиться наступне визначення.
Набор вершин графа називається максимальною незалежною системою (МНС), якщо будь-які дві вершини з цього набору не є суміжними і не можна включити в цей набір іншу вершину, щоб ця умова збереглася. Відмітимо, що знаходження МНС в графі досить просто: беремо проїзволную вершину, потім знаходимо будь-яку вершину, не суміжну з нею, потім знаходимо вершину, не суміжну з відібраними вершинами і так далі. Природно, що МНС в даному графові може бути багато і вони можуть містити різне число вершин. Перейдемо до опису алгоритму знаходження найкращого розфарбовування вершин графа. Хай маємо граф G, знайдемо в нім яку-небудь МНС, яку позначимо S1, і всі вершини, що входять в цю МНС, забарвимо в колір № 1. Далі, видалимо з даного графа всі вершини, що входять в цю МНС (разом з ребраребрамі), і для нового графа знову знайдемо МНС, яку позначимо S2. Ці нові вершини забарвимо в колір № 2, потім видалимо ці вершини з графа разом з відповідними ребрами і знову знаходимо МНС, яку забарвимо в колір № 3, і так далі. Можно доказать, что при любом способе осуществления этой процедуры придем к наилучшей раскраске и найдем некоторую функцию Гранди и хроматическое число данного графа [21].
Прімер. У графа (див. мал. 5.1) є 3 максимально незалежних систем вершин: {5}, {1,3} і {2,4}. Ясно, що при будь-якій процедурі знаходження хроматичного числа в цьому графові, отримаємо число 3.
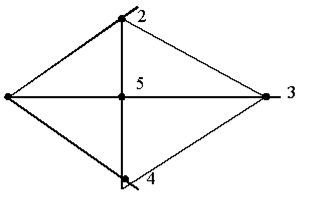
Рисунок 5.1 – Пример графа
Теорема. Якщо максимальна міра вершин в графі рівна r, то хроматичне число цього графа не перевершує r + 1. При цьому хроматичне число графа рівне r + 1 лише в двох випадках: по-перше, якщо граф є повним і, по-друге, якщо r = 2 і при цьому даний граф містить контур непарної довжини (такий граф змальований на мал. 5.2, максимальна міра його вершин – 2, а хроматичне число – 3). У всіх останніх випадках хроматичне число графа не перевершує максимальної міри вершин.
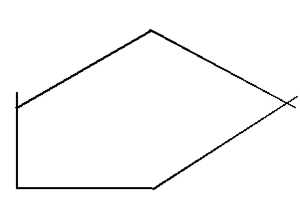
Рисунок 5.2 – Пример графа содержащий контур нечетной длины
Прімечаніє. Оцінка хроматичного числа, що дається цією теоремою, є досить грубою. Особливо наочно це виглядає на прикладі дерева для якого міра вершин може бути як завгодно велика, а хроматичне число дорівнює 2.
Рассматріваємиє питання повʼязані з відомою проблемою чотирьох фарб. Для того, щоб її сформулювати, нам знадобляться ще декілька визначень.
Граф називається плоским, якщо він намальований на плоскості, причому будь-які 2 ребра можуть перетинатися лише у вершині.
Графи називаються ізоморфними, якщо існує така нумерація вершин в цих графах, що вони мають одну і ту ж матрицю суміжності (фактично ізоморфні графи – це однакові графи, які відрізняються лише іншим зображенням) [21].
Граф називається планарним, якщо він ізоморфен плоскому графові. Таким чином, планарний граф можна змалювати на плоскості як плоский.
Можно довести (це не зовсім проста теорема), що хроматичне число планарних графів менше або рівне 5. Проте Августом де Морганом (1850) була висунута гіпотеза про те, що хроматичне число планарних графів менше або рівне 4. Цій проблемі було присвячено величезне число математичних робіт. Врештірешт, удалося звести цю проблему до дослідження вірності цієї гіпотези для чималого числа типів графів (близько 30 тис.), що і було зроблено за допомогою комп'ютерів (1976). Гіпотеза про чотири фарби виявилася справедливою, а сама проблема перейшла в завдання про спрощення доказу гіпотези про чотири фарби.
Отметім найвідомішу інтерпретацію проблеми про чотири фарби. Хай є географічна карта. Чи можна, використовуючи лише 4 фарби, змалювати цю карту так, щоб сусідні країни (що мають загальний кордон) були забарвлені в різний колір. Зрозуміло, що у відповідному графові вершинами є країни, а суміжними вершинами є сусідні країни. Ясно, що отриманий граф є планарним, і після 1976 р. відповідь на це питання є позитивною [21].
Заметім, що в теорії графів ставиться часто питання про реброве розфарбовування графів. Яке мінімальне число кольорів (це число інколи називають реброво-хроматичним) потрібне, щоб розфарбувати ребра графа так, що будь-які 2 суміжних ребра (тобто 2 ребра, що мають загальну вершину) були б забарвлені в різний колір Для реброво-хроматичного числа графа справедлива набагато точніша оцінка, ніж для просто хроматичного числа, а саме, вірна наступна, якоюсь мірою дивна, теорема.
Теорема Візінга. Якщо в графі максимальна міра вершин рівна r, то реброво-хроматичне число рівне або r, або r +1.
Заметім, що до цих пір немає «хороших» критеріїв для графів, коли ж саме реброво-хроматичне число рівне r, а коли r + 1 [22].
Очевідно, що простий алгоритм знаходження реброво-хроматичного числа (і відповідного розфарбовування ребер) полягає в наступному: по даному графові будуємо так званий подвійний граф: ребра графа відповідають вершинам нового (подвійного) графа, причому, якщо 2 ребра мають загальну вершину, то вони є суміжними і в подвійному графові сполучені ребром. Після цього розфарбовуємо щонайкраще вершини подвійного графа і, переходячи до «старого» графа, отримуємо (одну з можливих) найкращих ребрових розфарбовувань графів [24].
5.1 Алгоритм розпізнавання графів трьома агентами
Рассматріваємий алгоритм заснований на стратегії пошуку в глибину.
Ета стратегія така: агенти йдуть в глибину
, поки це
можливо, повертаються назад, шукають іншу дорогу з ще не відвіданими
вершинами і не пройденнимі ребрами. В разі виявлення суміжної вершини,
забарвленої в «чужий» колір, агент мітить всі перешийки з
поточної вершини в чужу область і повідомляє другому АД, через
агента-експериментатора, про необхідність розпізнавання помічених
перешийків. Поки другий АЇ розпізнає перешийки, перший АД не може
мітити нові перешийки. В разі відсутності інших можливих варіантів
переміщення, окрім як помітити новий перешийок, перший АД зупиняється
до того моменту, поки другий АД не розпізнає всі помічені перешийки.
Предлагаємая стратегія володіє рядом особливостей:
1) граф G агентам не відомий;
2) при обході графа G, агенти створюють неявну нумерацію пройденних вершин: при перших відвідинах вершини вона забарвлюється агентом A в червоний колір (у жовтий колір в разі агента B) і їй фактично ставиться у відповідність номер, рівний значенню змінної Сч_А для агента A (Сч_B для агента B ).
Відмітимо, що Сч_А і Сч_B набувають відповідно непарних і парних значень. На основі нумерації і відбувається відновлення графа шляхом побудови графа H ізоморфного G . В процесі обходу агенти будують неявні дерева пошуку в глибину. Відносно цих дерев всі ребра розділяються на деревинні (забарвлюються при першому проходженні по ним червоним або жовтим кольором), зворотні (не належать дереву і забарвлюються при першому проходженні в чорний колір) і ребра перешийки (сполучають дерева, побудовані різними агентами). Деревні ребра проходятся як мінімум 2 рази і при останньому проході забарвлюються агентами в чорний колір. Зворотні ребра проходятся один раз.А ось ребра перешийки проходятся кожним агентом по два рази: перший минулий по ньому агент мітить перешийок, забарвлюючи його в червоний колір в разі агента A (у жовтий колір в разі агента B ), другий минулий по ньому агент розпізнає перешийок і фарбує його в чорний колір [25].
Красниє (жовті) вершини графа G, на кожному кроці алгоритму, утворюють червоний (жовтий) якщо це не повернення для розпізнавання перешийків) – коротшає, при розпізнаванні зворотного ребра і перешийків – не змінюється. Вершина, в якої всі інцидентні ребра розпізнані, забарвлюється в чорний колір. Алгоритм закінчує роботу, коли червона і жовта дороги стають порожніми, а всі вершини чорними [23].
Обход графа. У роботі АД можна виділити 5 режимів:
I. Звичайний режим. АД рухається вперед по білих вершинах,
забарвлюючи вершини, ребра, що сполучають їх, і далекі інцидентори в
свій
колір. Якщо немає можливих доріг переміщення, то АД
повертається назад, забарвлюючи пройденниє вершини, ребра і ближні
інцидентори в чорний колір. Повернувшись в початкову вершину, АД
завершує роботу. На кожному кроці АД обмінюється даними з АЕ [24].
II. Розпізнавання зворотних ребер. Якщо при русі вперед було виявлено зворотне ребро, то агент припиняє роботу в звичайному режимі. АД переходить по зворотному ребру, забарвлюючи його в чорний колір, і по своїй дорозі повертається у вершину, в якій змінив режим роботи. Досягнувши цієї вершини, агент перемикається в звичайний режим роботи. На кожному кроці АД обмінюється даними з АЕ [24].
III. Позначка перешийків. Якщо в процесі обходу графа був виявлений перешийок, то за умови, що все раніше помічені даним АД перешийки були розпізнані, агент перемикається в режим позначки перешийків. У цьому режимі АД переходить по перешийку в чужу область, забарвлюючи ребро і далекий інцидентор в «свій» колір. На наступному кроці повертається по цьому перешийку, нічого не забарвлюючи, і шукає інші перешийки з цієї вершини. Помітивши всі перешийки, АЇ повідомляє про це АЕ, який у свою чергу, дає команду другому АЇ про необхідність розпізнавання помічених перешийків. По завершенню режиму позначки перешийків АЕ містить інформацію про кількість помічених перешийків [24].
IV. Розпізнавання перешийків. Отримавши від АЕ команду про необхідність розпізнавання перешийків, АД перемикається в режим розпізнавання перешийків. Якщо у цей момент агент працює в режимі розпізнавання зворотного ребра, то АД перемкнеться в режим розпізнавання перешийків, лише по завершенію розпізнавання зворотного ребра. У цьому режимі АД повертається назад по своїй дорозі до виявлення найближчої вершини, інцидентної поміченому перешийку. Під поміченим перешей кому розуміється ребро, в якого ближній інцидентор, ребро і далека вершина цього ребра забарвлені в «чужий» колір. Далі можливі два випадки: Помічено один перешийок. АД переходить по ньому в чужу область, забарвлюючи перешийок в «свій» колір, а далекий інцидентор в чорний. На наступному кроці повертається по цьому перешийку в свою область, забарвлюючи далекий інцидентор і перешийок в чорний колір. Далі рухається вперед по своїй дорозі, поки не повернеться у вершину, в якій було вироблено перемикання в режим розпізнавання перешийків. Помічено не менше двох перешийків. АД переходить по першому знайденому поміченому перешийку в чужу область, забарвлюючи його в «свій» колір, а далекий інцидентор в чорний. На наступному кроці АД повертається по цьому перешийку в свою область, забарвлюючи його в чорний колір, а обидва інцидентора в червоний. Далі АД рухається назад по своїй дорозі, поки не буде знайдений наступний помічений перешийок. Далі можливий два варіанти [23].
1. Наступний помічений перешийок не останній. АД переходить по знайденому перешийку, забарвлюючи його в «свій» колір, а далекий інцидентор в чорний. На наступному кроці АД повертається тому перешийку в свою область, забарвлюючи його і обидва інцидентора в чорний колір. І знову повертається назад по своїй дорозі до наступного поміченого перешийка.
2. Наступний помічений перешийок останній. АД переходить по знайденому перешийку, забарвлюючи його в «свій» колір, а далекий інцидентор в чорний. На наступному кроці АД повертається по цьому перешийку в свою область, забарвлюючи його в чорний колір, а обидва інцидентора в червоний. АД переходить по останньому перешийку в чужу область, забарвлюючи інцидентори в чорний колір. На наступному кроці АД переходить по першому розпізнаному перешийку в свою область, забарвлюючи інцидентори в чорний колір. Далі АД повертається у вершину, в якій було вироблено перемикання в режим розпізнавання перешийків.
V. Одночасне попадання два АД в одну білу вершину. При одночасному попаданні два АД в одну білу вершину, кожен АД забарвлює вершину наполовину, і вона стає червоно-жовтою. Агент B на наступному кроці відступає назад по своїй дорозі і переходить в режим позначки перешийків (при цьому ребро, по якому він повернувся вже пораховано як перший перешийок, а довжина жовтої дороги зменшена на одну вершину). Агент A бачить різноколірну вершину як свою, але при розпізнаванні забарвлює в чорний колір обидві половинки.
5.2 Відновлення графів за допомогою побудови на його вершинах нумерації
Задан граф G звʼязний, кінцевий, неорієнтований, без петель і ратних ребер, елементи якого можна мітити спеціальними фарбами. Заданий агент, який може пересуватися по графові з вершини у вершину, по ребру, що сполучає їх, «бачити» (сприймати) і аналізувати локальну інформацію про 1-околиці вершини, в якій він знаходиться, вибирати напрям руху і спосіб фарбування елементів на основі отриманої інформації про 1-околиці вершини. Спочатку передбачається, що агент поміщається в довільну вершину графа G, а всі його елементи помічені.
Требуєтся розробити такий метод обходу графа G і розфарбовування його елементів, щоб агент за отриманою інформацією про 1-околиць вершин зміг побудувати граф H ізоморфний графові G з точністю до міток на елементах графів.
Рассмотрім поставлені завдання:
1) побудова базового методу відновлення графа заснованого на побудові нумерації на його вершинах і побудова на основі цього методу поліноміального базового алгоритму;
2) дослідження тимчасової ємкісної складності базового алгоритму, а також кількість різних видів фарб використовуваних агентом для восстановленія графа;
3) аналіз базового алгоритму виділення основних етапів, знаходження модифікацій на яких досягаються кращі верхні оцінки тимчасової ємкісної складності;
4) знаходження класів графів і операцій над ними, які не погіршують верхню оцінку тимчасової складності виконання базового методу або його модифікацій.
Ідея базового методу. Обійти граф «в глибину», будуючи при цьому неявну нумерацію на вершинах графа G, і неявне дерево пошуку в глибину, відзначаючи вершини, ребра і інцидентори червоною фарбою і розбиваючи тим самим безліч ребер графа на дві безліч: деревинні і зворотні. За допомогою неявної нумерації відновлювати і мітити чорною фарбою зворотні ребра при першій їх появі у вершині, в якій знаходитися агент, а деревинні при першому проходженні по ним. Не явність нумерації полягає в тому, що явно номер не ставиться на вершину або інший елемент графа, а обчислюється на основі міток на елементах графів.
Основниє етапи «Базового алгоритму» [24]:
1. Ініціалізація.
2. Процедура ВПЕРЕД. Пошук раннє не пройденного білого ребра і перехід по ньому.
3. Процедура НАЗАД. Завершення повного дослідження вершини, перехід по червоному ребру, по якому агент вперше попав в дану вершину, позначка вершини і цього ребра чорною фарбою.
4. Процедура ВІДНОВЛЕННЯ. Відновлення зворотного ребра на основі неявної нумерації вершин графа і його позначка чорною фарбою.
5. Зупинка алгоритму після відновлення всіх вершин, деревних і зворотних ребер графа.
Модіфікациі базового алгоритму алгоритму.
Модіфікация 1. Агент, який проводить експеримент по восстановленію графа, може бути роздільний на двох агентів: агент дослідник (АД) і агент експериментатор (АЕ). Перший переміщається по відновлюваному графові, збирає інформацію про мітки на елементах графа, передає про свої переміщення і зміни міток на елементах графа АЕ. АЕ за повідомленнями АД будує представлення відновлюваного графа в своїй внутрішній пам'яті;
Модіфікация 2. Агент у відмінності від базового методу відновлює всі зворотні ребра кожної вершини;
Модіфікация 3. Агент відновлює зворотні ребра не при першій їх появі, а при попаданні агента у вершину з якої він може попасти лише в раніше відвідані;
Модіфікация 4. Всі вершини графа розбиваються на дві безліч: ординарні і не ординарні. Ординарні – вершини, валентність яких не більше ніж D, де D – заздалегідь відома константа. Інакше вершина не ординарна. Передбачається, що дві неординарні вершини не суміжних між собою;
Модіфікация 5. Агент реалізує неявну нумерацію за допомогою каменів з лічильниками, які після відновлення всіх зворотних ребер можна використовувати повторно.
Предложен базовий метод відновлення раніше невідомого графа з точністю до міток на елементах графів, за допомогою агента, що пересувається по ньому. На основі методу побудований «Базовий алгоритм», який використовує дві фарби і має тимчасову складність T(G), O(n) <=t(G) <=o(n3) [25].
Найдени операції над графами такі, що результуючий граф має верхню оцінку тимчасової складності, не гірше, ніж початкові.
Базовий метод допускає модифікації, які дозволяють отримати кращу оцінку тимчасової складності і спрощують агента, який пересувається по графові, проте, накладають додаткові обмеження на відновлюваний граф [25].
Модіфікация 1 – мобільний агент, O(n) <=t(G) <=o(n3).
Модіфікация 2 – O(n) <= T(G) <= O(n2).
Модіфікация 3 – породжує нові алгоритми відновлення графа, але не покращує складність алгоритмів.
Модіфікация 4 – агент кінцевий автомат, класи графів для яких T(G)=O(n), S(G)= O(n).
Модіфікация 5 – T(G)=O(n), агент використовує дві фарби і ht каменів, де ht – найбільша висота дерева при обході графа в глибину.
6. Метод порівняння мобільним агентом свого середовища і заданої карти
Вход: неорієнтовані звʼязні графи G1 і G2, вершини і ребра яких не відмічені (відмічені білою фарбою).
Виход: повідомлення графи ізоморфни чи ні.
Метод: паралельний рух в G1 і G2 по невідмічених або зелених ребрах через невідмічені або червоні вершини до тих пір, поки є хоч одна не чорна вершина в графі. При цьому пройденниє вершини і ребра забарвлюються відповідно до алгоритму.
1. Агент починає аналіз вершини v;
2. Якщо вершині v інцидентні декілька ребер, то агент ставить в v прапорець червоного кольору і йде в нову суміжну вершину, забарвлюючи ребро між вершинами зеленим кольором;
3. Агент на карті G2 позначає вершини і пройденниє ним ребра тим же кольорами і прапорцями, що і на середовищі G2;
4. Агент порівнює пройденниє вершини і ребра в карті G2 з пройденнимі вершинами і ребрами в середовищі G1,
5. Якщо досліджувана ділянка карти G2 збігається з дослідженою ділянкою середовища G1 і на карті є не пройденниє вершини і ребра, то переходить в 1;
6. Якщо досліджувана ділянка карти G2 збігається з дослідженою ділянкою середовища G1 і більше немає не пройденних вершин і ребер, то карта G2 ізоморфна G1 переходить до 10;
7. Інакше G1 не ізоморфен G2 переходить до 10;
8. Якщо число ребер q, інцидентних вершині v, рівне 1, то ставиться прапорець чорного кольору і агент слідує в суміжну їй вершину, забарвлюючи ребро зеленим кольором:
8.1 Якщо суміжна вершина має чорний прапорець, то переходить до 3, а потім до 5;
8.2 Інакше переходить до 3, а потім до 5;
9. Якщо число ребер q, інцидентних вершині v рівне 2, то розглядається така ситуация
9.1 Якщо у вершині v середовища G1 існує інцидентне їй зелене ребро і на одній з суміжних їй вершин коштує чорний прапорець, то агент ставить на вершині v чорний прапорець і переходить в суміжну вершину (відмічену білою фарбою, або червоним прапорцем), де немає чорного прапорця;
9.2 Переходить до 3–4;
9.3 Якщо у вершині v середовища G1 всі інцидентні нею ребра зелені і на обох суміжних вершинах коштують чорні прапорці, то у вершині v агент ставить чорний прапорець;
Переходить до 3, а потім до 6;
9.5 Якщо у вершині v середовища G1 всі інцидентні нею ребра білі, то вибирається суміжна вершина, на якій коштує червоний прапорець;
9.6 Інакше вибирає суміжну білу вершину і переходить до 1;
9.7 Якщо суміжна вершина вершині v з чорним прапорцем, то перехід до 6.
10. Кінець алгоритму.
Робота алгоритму представлена на малюнку 6.1
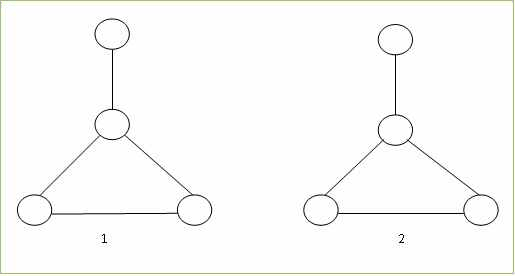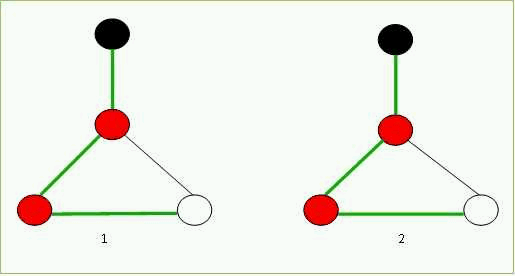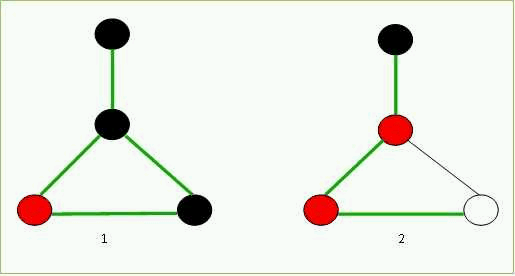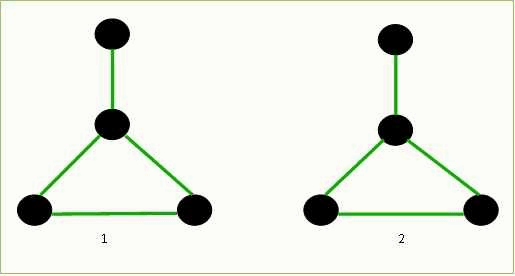
Рисунок 6.1 – Алгоритм порівняння мобільним агентом свого середовища і заданої карти
(анімація: 6 кадрів, 3 цикла повторення, 99 кілобайта)
(1 – середовище вивчення агента, 2 – карта агента)
Висновки
В процесі виконання даної роботи були вирішені наступні завдання:
1) вивчена карта як середовище руху агента;
2) розглянуті приклади існуючих топологічних карт;
3) розглянуті відомі алгоритми рішення;
4) розроблений метод порівняння карти і середовища;
5) вироблений ручний прорахунок методу.
В подальшому, результати використовуватимуться для написання дипломного проекту, в якому передбачається:
1) розробити програмну реалізацію описаного методу;
2) провести аналіз отриманих результатів і коректність отриманих алгоритмів.
Перелік посилань
- Сапунов С. В. Диссертация на соискание научной степени кандидата физико-математических наук: Анализ графов с помеченными вершинами / Сапунов С. В. – Донецк, 2007. – 180 с.
- Кудрявцев В. Б. Введение в теорию автоматов / Кудрявцев В. Б. – М. : Наука, 1985. – 320 с.
- Глушков В. М. Теория дискретных преобразователей / Глушков В. М. – Новосибирск: Наука, 1973. – 100 с.
- Кирильченко А. А. Теоретические аспекты организации интерпретирующей навигации мобильного робота / Кирильченко А. А. – М., 2002. – 37 с.
- Емеличев В. А. Лекции по теории графов / Емеличев В. А. – М. : Наука, 1990. – 384 с.
- Dudek G. Map validation and Robot Self-Location in a Graph-Like World / Dudek G // Robotics and Autonomous Systems. – 1997. – Vol. –22, – №2. – P. 159–178.
- Макконелл Д. Анализ алгоритмов. Вводный курс / Макконелл Д. – М. : Техносфера, 2002. – 304 с.
- Килибарда Г. Независимые системы автоматов в лабиринтах. Дискретная математика / Килибарда Г. – М. : Наука, 2003. – Т. 15, вып. 2, – 139 с.
- Килибарда Г., Кудрявцев В.Б., Ушчумличь Щ. Коллективы автоматов в лабиринтах // Дискретная математика. – 2003. – Т. 15, вып. 3. – С. 3–40.
- Кудрявцев В.Б., Ушчумличь Щ. О поведении автоматов в лабиринтах // Дискретная математика. – 1992. – Т. 4, вып. 3. – С. 3–28.
- Кудрявцев Г.Ю., О длине тестовых автоматов реализуемых эксперементов с автоматными лабиринтами // Дискретная математика. – 1992. – Т. 4, вып. 3. – С. 86–100.
- Грунский И.С., Олейник Р.И. Об отличимости инициальных лабиринтов конечными автоматами // Интеллектуальные системы. – 1999. – Т. 4, вып. 3–2. – С.243–272.
- Олейник Р.И. О контроле автоматных лабиринтов конечным автоматом // Труды ИМПММ НАНУ. – 2000. – Т. 5. – С. 107–114.
- Dudek G. Robotik exploration as graph construction / Dudek G // IEEE Transactions on on Robotics and Automation. – 1991. – Vol. 7, №6. – P, – 859–864.
- Dudek G. Map validation in a graphlike world / Dudek G // Proceedings of the 13th International Joint Conference on Artifical Intelligence (Chamdery, France, August 1993). – San Fransisco: Morgan Kaufmann Publishers Inc., 1993. – P. 1648–1653.
- Dudek G. Map validation and Robot Self-Location in a Graph-Like World / Dudek G // Robotics and Autonomous Systems. – 1997. – Vol. 22, P – 159–178.
- Dudek G., Jenkin M. Computational Principles of Mobile Robotics. / Dudek G., Jenkin M. // Robotics and Autonomous Systems. – 2000. – Cambridg. – P. 159–178.
- Капитанова Ю. В. Математическая теория проектирования вычислительных систем / Капитанова Ю. В. – М. : Наука, 1988. – 296 с.
- Shannon Cl.E. Presentation of a maze-solving machine // Cybernetics: Circular, Circular and Feedback Mechanisms in Biological and Social System: Transactions of VIII Conference (Mfrch 15–16, 1951). – New York: Josian Macy Jr. Foubdation, 1952, – P. 169–181.
- Грунский И.С., Курганский А.Н. Языки грыфов с помеченными вершинами // Труды ИМПММ НАНУ. – 2004. – Т. 9. – С. 53–60.
- Макконелл Д. Анализ алгоритмов. Вводный курс / Макконелл Д. – М. : Техносфера, 2002. – 304 с.
- Москинова Г.И. Дискретная математика. / Москинова Г. И. – М. : Логос, 2000. – 198 с.
- Будах Л. Лабиринты и автоматы. Проблемы кибернетики / Будах Л. – М.: Наука, 1978. – 94 с.
- Грунский И. С. Свойства языков, порождаемых неориентированными графами с отмеченными вершинами / Грунский И.С. // Материалы VIII Международного семинара «Дискретная математика и ее приложения» (2–6 февраля 2004 г.) – М. : Изд-во мех.-мат. ф-та МГУ, 2004. – С. 259–269.
- Емеличев В. А. Лекции по теории графов / Емеличев В. А. – М. : Наука, 1990. – 384 с.
