DonNTU   Masters' portal

Content

Introduction

It is often useful and clearly depict certain situations as a pattern consisting of dots (vertices) that represent the basic elements of the situation, and lines (edges) that connect certain pairs of vertices and depict relations between them. These pictures are known under the general name – graphs. Graphs are found in many areas under different names: "structure" in civil construction, "net" in electrical engineering, "sotsiohramy" in sociology and economics, "molecular structure" in chemistry, "roadmaps" and others. With the widespread use of graph theory in recent years intensively [15].

The rapid development of computer technology can solve all complex theoretical and applied problems, which in turn requires improved methods to solve them. Widespread technology of parallel and distributed computing provides new insights into many tasks, as well as techniques and algorithms that had seemed hopeless because of the high computational complexity. To the problem of high computational complexity are particular optimization problem. One of these problems is the problem of finding the shortest path on a graph. Problem has many practical applications, among them include finding the shortest path between the gardens, find your way data transmission that provides the minimum cost and minimum amount of time or the maximum transmission reliability in the distribution of information in a developed city.

1. The purpose and objectives of the study and expected results

The object of the research study is a two-level graph with N vertices. Each vertex of the graph of the first level is the second level graph with M vertices.

The subject of research is the method of finding shortest paths in labeled two-level graph.

The main objective is the design and software implementation of the method of finding the shortest path between the initial and any final vertices of the graph and the calculation of two-level quality (value) of the way.

The input data for the method is indicated by a two-level graph, the original data is marked shortest path between given nodes and the quality of the way.

2. Actuality

The problem of finding the shortest paths in a graph is a widely known and important for different applied. There are a number of algorithms for solving this problem. Recently, the problem is intensively studied for graphs of complex multilevel structure. In this paper the problem of finding shortest paths in labeled two-level graph from the initial vertex to some final.

Background for such complex graphs is that the applied problems to find the shortest path for traffic to pass through the paths of the city, complex road junctions. Therefore, the subject of this work is relevant enough.

3. Introduction to graphs

Graph – a set of objects with relationships between them. Objects are considered as vertices or nodes of the graph, and relationships – both arcs or edges.

For different regions use different types of graphs can oriyentovnistyu, restrictions on the number of links, and additional data on the tops or edges. A large number of structures that have practical value in mathematics and computer science, can be represented by graphs.

Earl G – is an ordered pair G = (V; E), for which the following conditions: V – set of vertices or nodes; E – set of pairs (in the case of an undirected graph – unordered) vertices, called rebramy.V and E are generally considered finite sets.

Key elements of the graph consisting of vertices, edges and arcs of the graph. The combination of these elements defines the concept: an undirected graph, directed graph and mixed graph.

Undirected graph - a graph (figure 3.1), for each edge which is immaterial order of its two end vertices.

Example of a labeled undirected graph

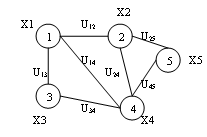
Figure 3.1 – Example of a labeled undirected graph

Directed graph – a graph for each edge by a significant order of its two end vertices. Directed graph shown in Figure 3.2, the edges are called arcs directed graph.

Example of a directed graph

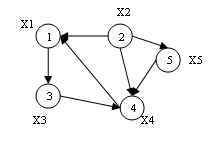
Figure 3.2 – Example of a directed graph

Mixed graph (figure 3.3) – a graph with both targeted and undirected edges. Each of these types of graph can contain one or more edges in which both ends converge at one vertex, these edges are called loops (figure 3.4).

Example of a mixed graph

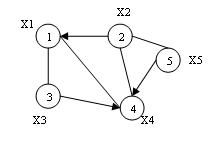
Figure 3.3 – Example of a mixed graph

Example of a mixed graph with loops

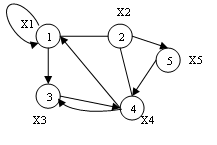
Figure 3.4 – Example of a mixed graph with loops

If a pair of vertices connected by several edges or arcs in one direction, then the edges (arcs) is called multiple (parallel). Arc or an edge connecting a vertex with itself is called a loop. Graphs without multiple arcs and loops is simple.

The degree of vertices – number of edges of the graph G, incidental to the top of x.

Weight ribs – the value supplied in accordance with this edge-weighted graph. Usually weight – a real number, in which case it can be interpreted as "long" edges.

Count, in which each edge (each arc) placed in line some non-negative integer called weight or length of edges (arcs) is called a weighted graph.

Paths in a graph is called a finite sequence of vertices in which every vertex is connected by an edge with the next in the sequence of vertices.

Arcs with common end vertices are called adjacent.

The path (or cycle) is called simple if the edges it does not recur; elementary if it is simple and tops it does not repeat.

Oriented path in directed graph called a finite sequence of vertices Vi, for which all pairs (Vi, V i + 1) is the (oriented) edges.

Path length (mashrutu) in the weighted graph is called the sum of the lengths of the links in this way (mashrutu).

Number k of edges in the path is called path length. It is said that this path connects vertices v1 and vk +1 or leads from the top of v1 to vertex vk +1.

Path length 0 is a sequence consisting of a single vertex.

The way in which all the edges are pairwise distinct, is called a chain. The way in which all intermediate vertices are pairwise distinct is called a simple chain.

The path is called a cycle, if it is the first and last vertices coincide. 

4. Review of existing algorithms for finding shortest paths in a graph

The problem of finding the optimal solution is basic in various fields of science and technology requires the development of effective solutions. Often optimization problems can be reduced to formal appearance and relationship components of the mathematical model represented as a graph. This approach allows the use of algorithms and tools of graph theory in the search for optimal solutions and to minimize analytical models optimality criteria. Solution of the problem then is to find the shortest paths between vertices of the graph.

A wide range of optimization problem is reduced to the description of the mathematical model of the system by means of graph theory to the definition of the physical content of an array of vertices and arcs that connect them. The optimal solution can then be found by the algorithm of graph theory by automated search for optimal solutions:

1) for finding the shortest path between two vertices using Dijkstra's algorithm, which requires the least time cost compared with similar algorithms;

2) finding the shortest path between all nodes of the graph by using Floyd;

3) Find the minimal path in the graph with edges of unit length can wave algorithm.

Conclusion

A new method for finding shortest paths in a two-level graph with vertices and arcs noticed that operates with two-level graph G without having to bring it up to standard view single-level graph, but using the method of local reduction graph.

As a result of the method of getting one or more optimal ways to pomitok and quality of these paths in a graph G.

It is easy to see that if all graphs Gi with one vertex, the method coincides with the previously developed algorithm for finding the shortest path in the graph labeled by a local reduction of the graph [5]. Thus, the proposed method is a significant generalization of the previously developed algorithm.

Generalization is the following.

1) Each vertex of a graph G is the graph Gi.

2) A calculation as a way of taking into account the weight of each vertex marks in this way and the weight of each edge marks at the time, as in [5] is performed only calculate weight labels of edges in the path.

3) Used algorithm [5] for graphs Gi.

Future we plan to improve the proposed method and its software implementation

When writing this master's work is not completed. Final completion: December 2014. Full text of the materials can be obtained from the author or his manager after that date.

References

1. Ногина Н.В. Синтез регулярного выражения языка, порожденного помеченным графом, методом его локальной редукции / Н.В. Ногина,  И.С. Грунский // Искусственный интеллект. – 2012. – №3. – С. 348-353

2.     Кристофидес, Н. Теория графов: алгоритмический подход / Н. Кристофидес. — М.: Мир, 1978. – 430 с.

3.   Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М.: Мир, 1979. – 536 с.

4.  Батищев Д.И. Многоуровневая декомпозиция гиперграфовых структур / Батищев Д.И., Старостин Н.В., Филимонов А.В. // Прилож. к журналу «Информационные технологии» №5(141). – М.: Новые технологии. – 2008. – 32 с.

5.   Ногина Н.В. Построение кратчайшего пути в помеченном графе при помощи локальной редукции графа / Н.В. Ногина, А.В. Билык // Сучасна інформаційна Україна: інформатика, економіка, філософія:  матеріали доповідей конференції, 26 квітня 2012 року. – Донецьк, 2012. – 316 с. – С. 76-79.

6. Бєлов В.Теорія графів / Бєлов В.– М. : Питер,1968. – 304 с.
Полат Е.С. Новые педагогические и информационные технологии / Полат Е.С. – М. : Akademia, 1999. – 401с.

7. Кузнєцов О.П. Дискретная математика для инженера / Кузнєцов О.П. – М. : Энергоатомиздат, 1988. – 703 с.

8. Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.

9. Смольяков Е.Р. Введение в теоpию гpафов / Смоляков Е.Р. – М. : МГТУ, 1992. – 705 с.

10. Hечепуpенко М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях / Hечепуpенко И.М. – М. : Hаука, 1990. – 202 с.

11. Романовский И.В. Алгоpитмы pешения экстpемальных задач / Романовский И.В. – М. : Hаука, 1977. – 506 с.

12. Землянухин В.Н. Задачи оптимизации на графах / В.Н. Землянухин, Л.Н. Землянухина. – М. : Наука, 2009. – 677 с.

13. Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение / В.А. Евстигнеев, В.Н. Касьянов. – М. : Наука, 1999. – 266 с.

14. Новиков Ф.А. Дискретная математика / Новиков Ф.А. – М. : Питер, 2001. – 301 с.

15. Интернет – источник. Алгоритмы на графах