ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст


Вступ

Часто буває корисно і наглядно зображувати деяку ситуацію у вигляді малюнка, який складається з точок (вершин), які зображують основні елементи ситуації, та ліній (ребер), які з’єднують визначені пари цих вершин та зображують зв’язки між ними. Такі малюнки відомі під загальною назвою – графи. Графи зустрічаються у багатьох областях під різними назвами: «структури» у громадянському будівництві, «мережа» в електротехніці, «соціограми» у соціології та економіці, «молекулярні структури» у хімії, «дорожні карти» та інші. Завдяки широкому використанню теорія графів в останні роки інтенсивно розвивається [15].

Бурхливий розвиток обчислювальної техніки дозволяє вирішувати все складніші теоретичні і прикладні задачі, що в свою чергу вимагає вдосконалення методів їх вирішення. Широке розповсюдження технології паралельних і розподілених обчислень дозволяє по-новому поглянути на вирішення багатьох задач, а також на методи і алгоритми, що раніше здавалися безперспективними через високу обчислювальну складність. До задач високої обчислювальної складності належать зокрема задачі оптимізації. Однією з таких задач є задача пошуку найкоротшого шляху на графі. Задача має багато практичних застосувань, до їх числа можно віднести пошук найкоротшого шляху між городами, пошук шляху передачі інформації, який забезпечує мінімальну вартість та мінімальну кількість часу передачі або максимальну надійність при розповсюдженні інформації у розгалуженій сіті.

Метою роботи є розробка методу пошуку найкоротшого шляху у поміченому дворівневому графі та програмна реалізація розробленого методу.

1. Мета і задачі дослідження та заплановані результати

Об'єктом дослідження в роботі є дворівневий граф з N вершинами. Кожна вершина графа першого рівня виступає графом другого рівня з M вершинами.

Предметом дослідження є метод пошуку найкоротших шляхів у позначеному дворівневому графі.

Основним завданням є розробка і програмна реалізація методу пошуку найкоротшого шляху між початковою і будь-який з фінальних вершинами дворівневого графа і розрахунок якості (вартості) цього шляху.

Вхідними даними для методу є позначений дворівневий граф, вихідними даними є позначка найкоротшого шляху між заданими вершинами, а також якість цього шляху.


2. Актуальність теми

Проблема пошуку найкоротших шляхів у графі є загально відомою та важливою для різних застосовань. Існує ряд алгоритмів для вирішення цієї задачі. В останній час ця проблема інтенсивно вивчається для графів складної багаторівневої структури. У даній роботі розглядається задача пошуку найкоротших шляхів у поміченому дворівневому графі від початкової вершини до деякої фінальної.

Актуальність проблеми для таких складних графів полягає в тому, що в прикладних задачах найкоротші шляхи потрібно знаходити для перевезень, які проходять через шляхи, міста, складні транспортні розв’язки. Тому тематика даної роботи достатньо актуальна.

3. Загальні відомості про графи

Граф – це сукупність об'єктів із зв'язками між ними. Об'єкти розглядаються як вершини, або вузли графу, а зв'язки – як дуги, або ребра.

Для різних областей використання види графів можуть відрізнятися орієнтовністю, обмеженнями на кількість зв'язків і додатковими даними про вершини або ребра. Велика кількість структур, які мають практичну цінність в математиці та інформатиці, можуть бути представлені графами.

Граф G – це впорядкована пара G = (V;E), для якої виконуються наступні умови: V –множина вершин або вузлів; E – множина пар (у випадку неорієнтованого графа – невпорядкованих) вершин, які називають ребрами.V і E зазвичай вважаються скінченними множинами.

Основні елементи графа складаються з вершин графу, ребер графу та дуг графу. Сполучення цих елементів визначає поняття: неорієнтований граф, орієнтований граф та змішаний граф.

Неорієнтований граф – це граф (рисунок 3.1), для кожного ребра якого несуттєвий порядок двох його кінцевих вершин.

Приклад поміченого неорієнтований графа

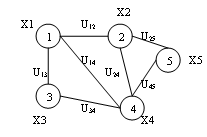
Рисунок 3.1 – Приклад поміченого неорієнтованого графа

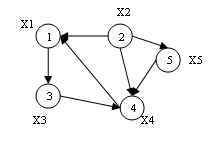
Орієнтований граф – це граф, для кожного ребра якого істотний порядок двох його кінцевих вершин (рисунок 3.2).


       Приклад орієнтованого графа

Рисунок 3.2 –  Приклад орієнтованого графа

 

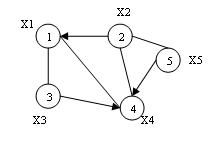
Змішаний граф (див. рис. 3.3) – це граф, що містить як орієнтовані, так і неорієнтовані ребра. Кожної з перерахованих видів графа може містити одне або кілька ребер, у яких обидва кінці сходяться в одній вершині, такі ребра називаються петлями (див. рис. 3.4).


     Приклад змішаного графа

 Рисунок 3.3 – Приклад змішаного графа

Приклад змішаного графа з петлями

 Рисунок 3.4 –  Приклад змішаного графа з петлями

 

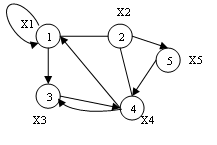
Якщо пара вершин сполучається кількома ребрами чи дугами одного напрямку, то ребра (дуги) називають кратними (паралельними). Дуга чи ребро що сполучає вершину саму із собою називається петлею. Граф без кратних дуг і петель називається простим.

Ступінь вершини – кількість ребер графа G, інцидентних вершині x.

Вага ребра – значення, поставлено у відповідність даному ребру зваженого графа . Зазвичай вага  – дійсне число, в такому випадку його можна  інтерпретувати як "довжину" ребра.

Граф, у якому кожному ребру (кожній дузі) поставлено у відповідність певне невід'ємне число, яке називають вагою або довжиною ребра (дуги), називають зваженим графом.

Шляхом у графі називають кінцеву послідовність вершин, в якій кожна вершина з'єднана ребром з наступною в послідовності вершин. 

Дуги, які мають спільні кінцеві вершини, називаються суміжними.

Шлях (або цикл) називають простим, якщо ребра в ньому не повторюються; елементарним, якщо він простий і вершини в ньому не повторюються.

Орієнтованим шляхом в Орграф називають кінцеву послідовність вершин V i, Для якої всі пари (Vi,V i + 1) є (орієнтованими) ребрами.

Довжиною шляху (машруту) у зваженому графі називають суму довжин ланок цього шляху (машруту).

Кількість k ребер у шляху називається довжиною шляху. Кажуть, що цей шлях з’єднує вершини v1 і vk +1 або веде з вершини v1 у вершину vk +1.

Шляхом довжини 0 вважається послідовність, що складається з єдиної вершини.

Шлях, в якому всі ребра попарно різні, називається ланцюгом. Шлях, в якому всі проміжні вершини попарно різні, називається простим ланцюгом.

Шлях називають циклом, якщо в ньому перша та остання вершини збігаються. 

  4. Огляд існуючих алгоритмів для пошуку найкоротших шляхів у графі

Проблема пошуку оптимальних рішень є базовою у різних галузях науки і техніки і потребує розробки засобів ефективного вирішення. Часто оптимізаційні задачі можна звести до формалізованого вигляду і взаємозв’язок складових частин математичної моделі подати у вигляді графа. Такий підхід дозволяє використовувати алгоритми і засоби теорії графів у процесі пошуку оптимальних рішень і мінімізації аналітичних моделей критеріїв оптимальності. Розв’язок задачі тоді зводиться до пошуку найкоротших шляхів між вершинами графа.

Широке коло оптимізаційних задача зводиться до опису математичної моделі системи за допомогою засобів теорії графів з визначенням фізичного змісту масиву вершин та дуг, що їх сполучають. Оптимальне рішення тоді може бути знайдене за визначеним алгоритмом теорії графів з допомогою автоматизованої системи пошуку оптимальних рішень:

1) для пошуку  найкоротшого шляху між двома вершинами графа використовується алгоритм Дейкстри, який потребує найменше часових затрат порівняно з подібними алгоритмами;

2) пошук найкоротших шляхів між усіма вершинами графа здійснюється за допомогою алгоритма Флойда;

3) знайти мінімальний шлях в графі з ребрами одиничної довжини дозволяє хвильовий алгоритм.

5. Метод побудови найкоротших шляхів у дворівневому графі

Розглядаються зв'язні неорграфи зі скінченими множинами вершин Q і ребер E, що не мають петель. Ребро – це є пара вершин (q, u). Ребра графа G відмічено мітками з множини Y, виділено початкову вершину та множину фінальних вершин. Таким чином, G=(Q, E, Y, ρ, q0, F), де:

Q – скінченна множина вершин графа G ;

E – множина ребер графа G;

Y – множина поміток ребер графа G;

ρ: E→Y – функція розмітки ребер графа G;

q0 – початкова вершина графа G;

F–множина фінальних вершин графа G.

Граф G будемо називати графом першого рівня. Кожна вершина q  графа G є графом Gi – графом другого рівня без петель і кратних дуг, в якому вершини і ребра відмічено мітками з множин M і P відповідно. Так, Gi =(Ti, Di, Mi, Pi, µ , t,  n0, fi), де:

Ti – скінченна множина вершин графа Gi;

Di – множина дуг графа Gi;

Mi – множина поміток вершин графа Gi; 

Pi – множина поміток дуг графа Gi;

µ: T→M – функція розмітки вершин графа Gi;

t: D→P –  функція розмітки дуг графа Gi;

n0 – початкова вершина графа Gi;

fi – фінальна вершина графа Gi.

Вершина графа Gi  має наступний вигляд: (qi; tj), де  qi  – номер вершини  графа G, а  tj – номер вершини графа Gi. Дуга графа G з'єднує унікальну пару вершин різних графів Gi.

Кожній вершині qi графа G поставимо у відповідність число Z(qi) – якість цієї вершини.

Шляхом у графі G назвемо скінченну послідовність l = q1 e1 q2 e2…ek-1 qk, де qk, а ei – дуга, початком якої є вершина qi, а кінцем – qi+1.

Шляхом у графі Gi. назвемо скінченну послідовність s = (q1; ti) d1 (q2; tj)d2…dk-1(qk; tn), де (qi; tj)Î Ti, а di – дуга, початком якої є вершина (qi; tj), а кінцем – (qi+1; tn).

Відмітка шляху s – це послідовність відміток w(s)=m1 p1 m2 p2…pk-1 mk, де mi= µ(Ti), pi =t (di).

Генеральним шляхом назвемо послідовність I= (q1; ti) x1 (q2; tj)x2…xk-1(qk; tn), де (qi; tj) Î Ti, а xi  може бути дугою ei графа G або дугою di графа Gi.

Відмітка шляху I – це послідовність відміток w(I)=a1 b1 a2 b2…bk-1 ak, де ai= µ(Ti), bi = ρ(ei) або bi = t (di).

Вагою генерального шляху I між вершинами qi та qj, будемо називати вагу шляху між вершинами (qi; tn)та (qj; tm) і визначимо її величину за  формулою на рисунку 5.1.

Вага шляху

Рисунок 5.1 –  Формула ваги генрального шляху

Якість генерального шляху I визначимо через величину dis (I) за формулою на рисунку 5.2.

Якість шляху

Рисунок 5.2 –  Формула якості генерального шляху

Для вершини qi визначимо множину Pre(qi) = (qj | (qj, qi)=ei) та множину Post(qi) = (qj | (qi, qj)=ei).

Метод побудови найкоротших шляхів у дворівневому графі.

Вхідні дані: помічений дворівневий граф G з початковою і множиною фінальних вершин.

Вихідні дані: одна або декілька поміток найкоротших шляхів, якість цих шляхів.

Крок 1.

1.1)  Для неорієнтованих графів G для кожного ребра між парою вершин qi та qj вводиться дві дуги: (qi,qj) та (qj,qi).

1.2)  У список вершин графа G вводиться фіктивна кінцева вершина fin, а в список дуг – дуга з кожної фінальної вершини qi у вершину fin. Ця дуга позначається відміткою µ(qi;tj).

1.3)  Створюємо представлення графа G у вигляді списку дуг з їх відмітками і вагою, при цьому відмітки відповідних вершин графів Gi. переносяться на дуги графа G (наприклад, якщо помітками двох вершин і дуги між ними будуть відповідно (qi,tn),(qj,tm) та xw, то після перенесення поміток вершин на дугу, помітка дуги матиме наступний вигляд: (qi,tn) xw (qj,tm)).

1.4)  Для кожного ребра графа Gi між парою вершин (qi; tn) та (qj; tm) вводиться дві дуги: ((qi; tn);(qj; tm)) та ((qj; tm);((qi; tn)), при цьому відмітки вершин переносяться на дуги.

Крок 2. If в графі G існує хоч одна  вершина, що не є початковою або фінальною, з якої виходить хоч одна дуга в фінальну, then go to Крок 3, else go to Крок 7.

Крок 3. Вибираємо qi =Pre(fin); q:= qi.

Крок 4. If q ≠ q0 then видаляємо вершину q та усі вхідні та вихідні з неї дуги. If при цьому є деякий шлях qi ek q e qj, де qi=Pre(q) та qj=Post(q), then у граф додається дуга (qi ,qj) з відміткою ek опеератор e, отриманою за допомогою операції  з'єднування.

Else, якщо q = q0 go to Крок 2.

Крок 5. Видаляємо ті петлі, в помітках яких початок і кінець співпадає.

Крок 6. Заміна оператора з'єднування.

На кроках 4 – 6 відбувається видалення однієї вершини.

Для вершин, помітки яких з'єднані оператором з'єднування (наприклад, (qi; tn) W (qi; tm)) працює алгоритм [5], який шукає оптимальний шлях між цими вершинами (наприклад, між tn і tm, де tn – визначимо як початкову вершину, а tm – як фінальну). Для цього створюємо представлення відповідного графа Gi ( tn, tm) у вигляді списку дуг з їх відмітками і вагою.

If в результаті роботи алгоритму [5] оптимальний шлях знайдено, then поміткою цього шляху замінюємо оператор з'єднування разом з двома помітками, які він з'єднує.

If оптимальних шляхів декілька, then в список дуг графа G додається така ж сама дуга, але, відповідно, з іншою поміткою.

Else, якщо шляху не існує, then видаляємо дугу (qi ,qj).

Крок 7. Видаляємо усі вершини, що не є початковою або фінальною та усі вхідні та вихідні з них дуги. В результаті одержуємо граф, що складається лише з двох вершин: початкової та фінальної.

Обчислюємо якість шляху QPath для усіх дуг графа G, які з'єднують ці вершини. Оберемо найменше значення QPath, яке і визначає оптимальний шлях у графі. Якщо найменших значень QPath декілька, то результатом буде декілька шляхів з цими значеннями.

Приклад роботи методу побудови найкоротшого шляху в дворівневому графі представлений на рисунку 5.3.

Приклад роботи методу побудови найкоротшого шляху в дворівневому графі

Рисунок 5.3 – Приклад роботи методу на дворівневому графі складається з трьох вершин
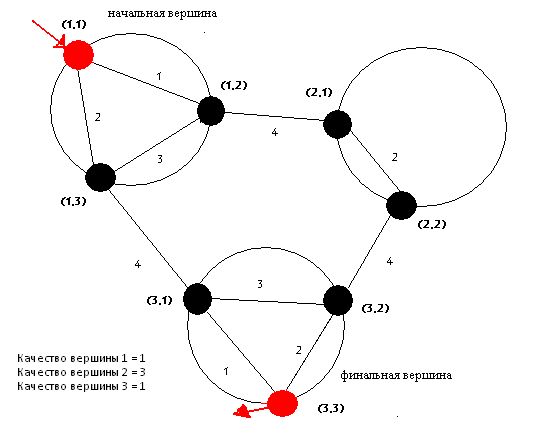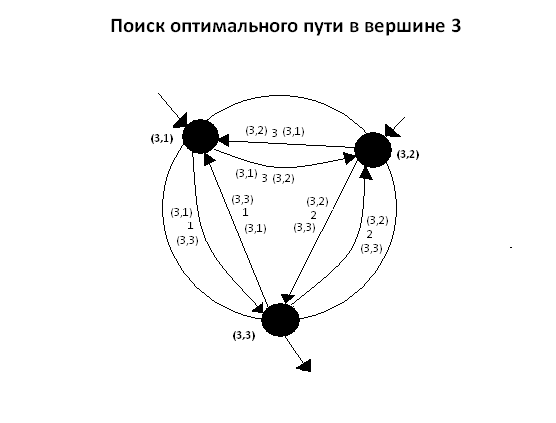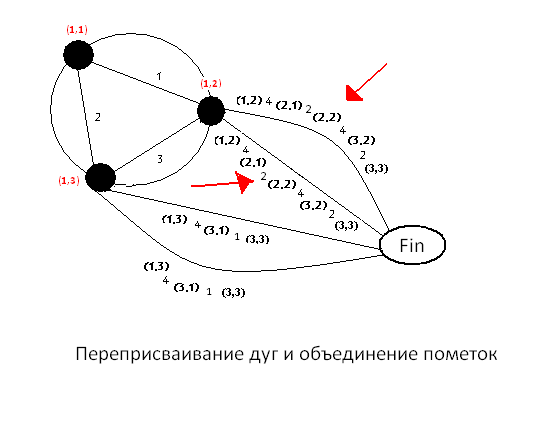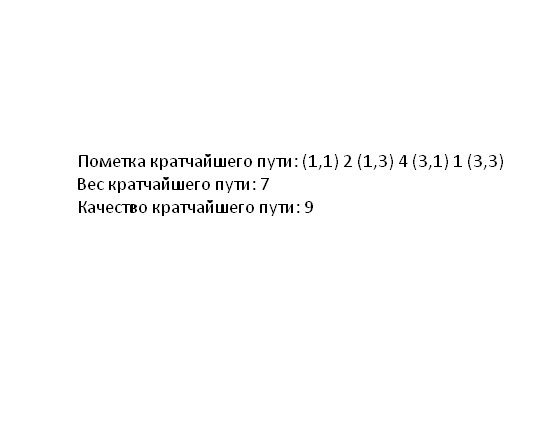
(анімація: 25 кадрів, 5 циклів повторення, 166 кілобайт)

Висновки

Запропоновано новий метод пошуку найкоротших шляхів у дворівневому графі з поміченими вершинами і дугами, який працює з дворівневим графом G без необхідності приводити його до стандартного вигляду однорівневого графа, але при цьому використовується метод локальної редукції графа.

В результаті застосування методу отримуємо одну або декілька поміток для оптимальних  шляхів і якість цих шляхів у графі G.

Легко бачити, що у випадку, коли всі графи Gi мають по одній вершині, розроблений метод співпадає з раніше розробленим алгоритмом пошуку найкоротшого шляху у поміченому графі методом локальної редукції графа [5]. Таким чином, запропонований метод є суттєвим узагальненням раніше розробленого алгоритму.

Узагальнення полягає у наступному.

1)  Кожна вершина графа G є графом Gi.

2)  Проводиться обчислення якості шляху з урахуванням ваги помітки кожної вершини у цьому шляху та помітки ваги кожного ребра у той час, як у [5] виконується тільки обчислення ваги  позначок ребер у шляху.

 3) Використовується алгоритм [5] для графів Gi.

Надалі планується удосконалення розробленого методу і його програмна реалізація

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2014 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Перелік посилань

1. Ногина Н.В. Синтез регулярного выражения языка, порожденного помеченным графом, методом его локальной редукции / Н.В. Ногина,  И.С. Грунский // Искусственный интеллект. – 2012. – №3. – С. 348-353

2.     Кристофидес, Н. Теория графов: алгоритмический подход / Н. Кристофидес. — М.: Мир, 1978. — 430 с.

3.   Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М.: Мир, 1979. – 536 с.

4.  Батищев Д.И. Многоуровневая декомпозиция гиперграфовых структур / Батищев Д.И., Старостин Н.В., Филимонов А.В. // Прилож. к журналу «Информационные технологии» №5 (141). – М.: Новые технологии. – 2008. – 32 с.

5.   Ногина Н.В. Построение кратчайшего пути в помеченном графе при помощи локальной редукции графа / Н.В. Ногина, А.В. Билык // Сучасна інформаційна Україна: інформатика, економіка, філософія:  матеріали доповідей конференції, 26 квітня 2012 року. – Донецьк, 2012. – 316 с. – С. 76-79.

6. Бєлов В.Теорія графів / Бєлов В.– М. : Питер,1968. – 304 с.
Полат Е.С. Новые педагогические и информационные технологии / Полат Е.С. – М. : Akademia, 1999. – 401с.

7. Кузнєцов О.П. Дискретная математика для инженера / Кузнєцов О.П. – М. : Энергоатомиздат, 1988. – 703 с.

8. Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.

9. Смольяков Е.Р. Введение в теоpию гpафов / Смоляков Е.Р. – М. : МГТУ, 1992. – 705 с.

10. Hечепуpенко М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях / Hечепуpенко И.М. – М. : Hаука, 1990. – 202 с.

11. Романовский И.В. Алгоpитмы pешения экстpемальных задач / Романовский И.В. – М. : Hаука, 1977. – 506 с.

12. Землянухин В.Н. Задачи оптимизации на графах / В.Н. Землянухин, Л.Н. Землянухина. – М. : Наука, 2009. – 677 с.

13. Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение / В.А. Евстигнеев, В.Н. Касьянов. – М. : Наука, 1999. – 266 с.

14. Новиков Ф.А. Дискретная математика / Новиков Ф.А. – М. : Питер, 2001. – 301 с.

15. Інтернет – джерело. Алгоритми на графах