Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Научная новизна в области применения
- 4. Общая постановка проблемы
- 4.1 Основные факторы, влияющие на выбор страхового пакета
- 4.2 Поиск решений в иерархии пространств
- 4.3 Поиск решений в альтернативных пространствах
- 4.4 Поиск решений с использованием нескольких моделей
- 4.5 Нейлоровские диагностирующие системы
- 4.6 Выбор метода решения задач
- Выводы
- Список источников
Введение
Современные страховые компании предоставляют широкий спектр услуг по страхованию транспортных средств, и клиентам не всегда бывает легко разобраться во всех существующих предложениях и подобрать наиболее подходящий им вид страхования.
Данная работа представляет собой описание по разработке прототипа экспертной системы, целью которой является помощь в определении оптимального варианта страхования. Данная система призвана заменить эксперта-консультанта в выбранной предметной области.
1. Актуальность темы
В связи с ростом технических возможностей современных вычислительных систем появляется все больше и больше возможностей по обработке данных. Технический прогресс не обошел стороной страховые компании. Во многих зарубежных компаниях используется большое количество сложных скоринговых систем. Актуальность обусловлена ростом потребности Украинских страховых компаний в эффективном андеррайтинге в связи с развитием страхового рынка и фактически полным отсутствием внедренных скоринговых систем.
2. Цель и задачи исследования, планируемые результаты
Цель: Разработка компьютеризированной скоринговой системы поддержки принятия решений страхования автомобилей.
Основные задачи исследования:
- Исследование процессов андеррайтинга
- Изучение факторов, влияющих на выбор страхового портфеля
- Нахождение оптимального страхового портфеля
- Исследование методов прогнозирования страховых случаев
- Выбор оптимального метода для создания ЭС
3. Научная новизна в области применения
Скоринговой система поддержки принятия решений страхования автомобилей создает широкий спектр возможностей по удобному подбору страхового пакета без непосредственного контакта с представителем страховой компании. На сегодняшний день существует большое разнообразие алгоритмов подбора страхового пакета, дающих оптимальные результаты. Однако, в Украине, не существует одного внедренного универсального алгоритма, подходящего для любого класса данных, а также выявляющего вероятность мошенничества при страховании. Кроме того, различные алгоритмы ведут себя по-разному при обработке достаточно больших объемов данных. В связи с этим целесообразно разработать алгоритм, который мог бы одновременно подбирать страховые пакеты для клиентов, а также выявлять вероятность мошенничества со стороны клиента.
4. Общая постановка проблемы
4.1 Основные факторы, влияющие на выбор страхового пакета
- Размер страховой суммы;
- Количество страховых случаев;
- Марка автомобиля – частота ДТП;
- Марка автомобиля – частота угонов;
- Наличие и размер франшизы;
- Возраст водителя;
- Опыт вождения;
- Год выпуска авто;
- Страна производитель авто;
- СТО владельца;
4.2 Поиск решений в иерархии пространств
Методы поиска решений в одном пространстве обычно делятся на:
- поиск в пространстве состояний;
- поиск методом редукции;
- эвристический поиск;
- поиск методом "генерация-проверка".
Рассмотрим поиск методом редукции
При поиске методом редукции решение задачи сводится к решению совокупности образующих ее подзадач. Этот процесс повторяется для каждой подзадачи до тех пор, пока каждая из полученного набора подзадач, образующих решение исходной задачи, не будет иметь очевидное решение. Процесс решения задачи разбиением ее на подзадачи можно представить в виде специального направленного графа G, называемого И/ИЛИ-графом; Каждой вершине этого графа ставится в соответствие описание некоторой задачи (подзадачи). В графе выделяют два типа вершин: конъюнктивные вершины и дизъюнктивные вершины.
Решение задачи при поиске методом редукции (при поиске в И/ИЛИ-графе) сводится к нахождению в И/ИЛИ-графе решающего графа.
Цель процесса поиска в И/ИЛИ-графе - показать, что начальная вершина разрешима, т.е. для этой вершины существует решающий граф[2].
4.3 Поиск решений в альтернативных пространствах
Рассмотренные выше методы поиска исходят из молчаливой предпосылки, что знания о предметной области и данные о решаемой задаче являются точными и полными и для них справедливо следующее:
- все утверждения, описывающие состояние, являются истинными;
- применение оператора к некоторому состоянию формирует некоторое новое состояние, описание которого состоит только из истинных фактов.
Однако при решении любых практических задач и особенно при решении неформализованных задач распространена обратная ситуация. Эксперту приходится работать в условиях неполноты и неточности знаний (данных) и, как правило, в условиях дефицита времени. Когда эксперт решает задачу, он использует методы, отличающиеся от формальных математических рассуждений. В этом случае эксперт делает правдоподобные предположения, которые он не может доказать; тем самым вопрос об их истинности остается открытым. Все утверждения, полученные на основе этих правдоподобных предположений, также не могут быть доказаны [2].
4.4 Поиск решений с использованием нескольких моделей
Все методы поиска, рассмотренные до сих пор, использовали при представлении проблемной области какую-то одну модель, т.е. рассматривали область с какой-то одной точки зрения. При решении сложных задач в условиях ограниченных ресурсов использование нескольких моделей может значительно повысить мощность системы. Объединение в одной системе нескольких моделей дает возможность преодолеть следующие трудности:
- переход с одной модели на другую позволяет обходить тупики, возникающие при поиске в процессе распространения ограничений;
- использование нескольких моделей позволяет в ряде случаев уменьшить вероятность потери хорошего решения (следствие неполного поиска, вызванного ограниченностью ресурсов) за счет конструирования полного решения из ограниченного числа частичных кандидатов путем их расширения и комбинации;
- наличие нескольких моделей позволяет системе справляться с неточностью (ошибочностью) данных.
Следует отметить, что использование нескольких моделей требует дополнительных знаний о том, как создавать и объединять различные точки зрения.
4.5 Нейлоровские диагностирующие системы
Разработанная К. Нейлором концепция построения ЭС основана на общей байесовской схеме. Основные принципы, реализованные в данной ЭС, включают:
- введение верхних и нижних порогов для вероятностей гипотез;
- учет неопределенностей, заключенных в реакции пользователей;
- введение цен свидетельств, определяющих сценарий диалога с пользователем.
Первое усложнение, которое вводится в общую схему байесовского подхода, связано с использованием верхних и нижних порогов для вероятностей отдельных гипотез. Если вероятность Р(Н) после учета всех свидетельств превосходит верхний порог М1(Н):
Р(Н)>М1(Н),
то гипотеза Н принимается как основа для возможного заключения. Если же
Р(Н) < М2(Н),
где М2(Н) — нижний порог, то гипотеза Н отвергается как неправдоподобная.
Есть основания устанавливать верхние и нижние пороги M1, М2 индивидуально для каждой гипотезы в соответствии с имеющейся в СППР базой знаний и максимальных возможных уровней вероятностей гипотез с учетом всех принципиально возможных свидетельств. Например, можно полагать
М1(Н) = 0,9РМАХ(Н), М2(Н) = 0,5М1(Н),
где РМАХ(Н) — максимальная возможная вероятность, достижимая для данной гипотезы, при условии, что все свидетельства, имеющиеся в базе знаний и связанные с этой гипотезой, будут подтверждены пользователем в пользу гипотезы Н.
Величины РМАХ(Н) для всех Н, так же как и М1(Н) , М2(Н) , очевидно, могут быть вычислены заранее и также включены в базу знаний СППР.
Учет неопределенности, заключенной в ответах пользователя на вопросы СППР, является важным моментом в организации диалога. В идеале мы могли бы предположить, что на вопрос СППР пользователь отвечает либо "да", либо "нет" (есть высокая температура у пациента, нет высокой температуры и т. д.), т. е. выполняется данное свидетельство Е или не выполняется.
Более реалистичной является ситуация, когда пользователь по какой-либо причине либо хочет уклониться от ответа (если, например, вопрос слишком сложен и не соответствует квалификации пользователя в данной предметной области), либо стремится дать не слишком определенный ответ. Например, если задается вопрос о наличии повышенной температуры у пациента, то необходимо дать пользователю возможность проранжировать степень повышения температуры, например, в соответствии с 11-балльной шкалой:
- -5 соответствует НЕТ;
- 0 соответствует НЕ ЗНАЮ;
- +5 соответствует ДА.
Присутствуют и все промежуточные целые значения шкалы от -5 до +5.
В результате каждое свидетельство Е будет оцениваться по этой шкале на основании ответа пользователя
В соответствии с байесовским подходом после обработки очередного свидетельства Е мы вычисляли вероятность Р(Н / Е) и заменяли ею предыдущую вероятность Р(Н). Теперь мы должны предложить способ вычисления не Р(Н / Е), а Р(Н / R). Это может быть выполнено следующим образом. Во-первых, случай R = 5 должен соответствовать вероятности Р(Н / Е), вычисленной по формуле Байеса. Во-вторых, вариант R =-5 должен соответствовать величине Р(Н / Е). Последняя вероятность может быть найдена из соотношений:
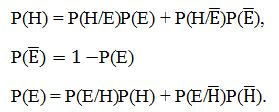
В-третьих, случай R = О (НЕ ЗНАЮ), очевидно, не должен изменять априорную вероятность Р(Н) и поэтому здесь имеем:
Мы получили три характерные точки на графике Р(Н / R)как функции R, Промежуточные значения Р(Н / R)предлагается восстанавливать с помощью линейной интерполяции. Таким образом, для любого не R принадлежащему R мы получаем соответствующее значение Р(Н /R), что и требовалось. При этом максимальное значение Р(Н / R) будет равно Р(Н / Е) и соответствовать случаю R = 5, как и указывалось ранее [3].
4.6 Выбор метода решения задач
Так как основной задачей разработки данной СППР является подбор оптимального пакета страхования, то считаю логичным использовать нейлоровские диагностирующие системы, так как благодаря такой структуре мы можем с определенными вероятностями определить пригодность страхового пакета для каждого автовладельца.
Используем метод Нейлора к нашей области и составим образец БЗ для СППР страхования автомобилей.
Гипотезы Hi:
Страховой пакет 1; 0,1; 5; (1; 0; 0.99); (2; 0,7; 0,05); (4; 0,2; 0,5); (5; 0; 0,99); (6; 1; 0,01);
Страховой пакет 2; 0,05; 2; (2; 1; 0,01); (6; 0,9; 0,02);
Страховой пакет 3; 0,01; 3; (3; 0,9; 0,1); (4; 0,25; 0,5); (6; 0,9; 0,02);
Страховой пакет 4; 0,01; 2; (4; 0,01; 0,5); (6; 0,9; 0,02).
Дадим расшифровку приведенных записей. Априорная вероятность того, что владельцу авто подойдет страховой пакет 1, равна 0,1. В данной базе знаний со страховым пакетом 2 связаны два (2) критерия.
Первый критерий — высокая страховая сумма. Вероятность высокой страховой суммы здесь положена равной 1. Вероятность того, что при высокой страховой сумме этот пакет не подойдет равна 0,01.
Второй критерий — марка модели. Вероятность дорогой марки авто при выборе страхового пакета 1 равна 0,9. Вероятность того, что при дорогой марке авто этот пакет не подойдет равна 0,02.
Свидетельства Ei:
- Количество страховых случаев; Много страховых случаев?
- Размер страховой суммы; Большая страховая сумма?
- Марка автомобиля – частота угонов; Частота угонов?
- Год выпуска авто; Новый автомобиль?
- Страна производитель авто; Страна производителя авто?
- Марка автомобиля – частота ДТП; Дорогая марка автомобиля?
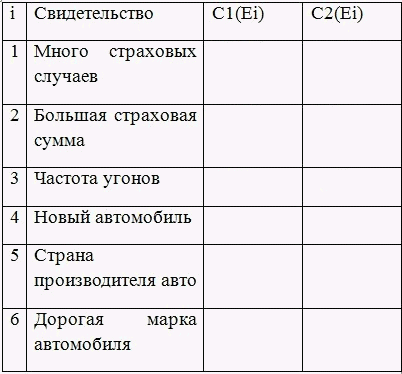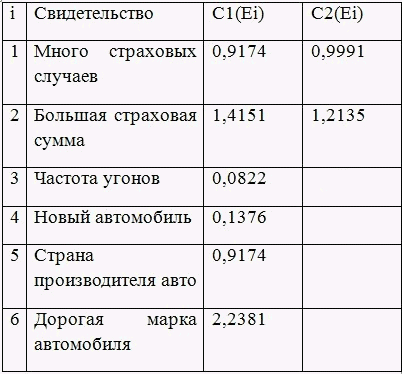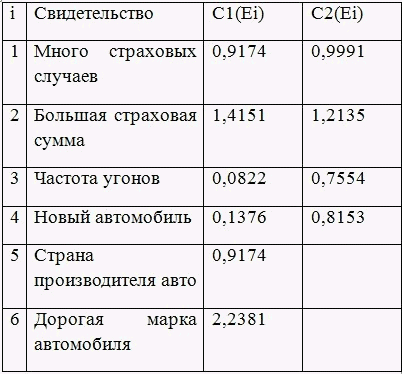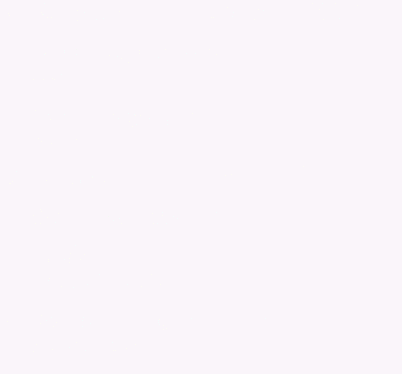
Таблица 1 – Цены свидетельств
(анимация: 7 кадров, 30 циклов повторения, 146 килобайт)
Согласно вычисленным исходным ценам свидетельств C1(Ei) первым будет всегда задаваться вопрос, связанный со свидетельством Е6 (у него максимальная цена 2,2381):
Дорогая марка автомобиля?
При ответе пользователя ДА (R = 5) мы можем пересчитать массив P(Hi) и вычислить новые цены свидетельств C2(Ei). С учетом новых цен свидетельств будет задан следующий вопрос, связанный со свидетельством Е2 (у него максимальная цена 1,2135).
При этом сообщение о том, что марка автомобиля дорогая, привело к существенному увеличению цен и остальных свидетельств, что выглядит весьма естественно.
Выводы
Проанализированы методы создания СППР страхования автомобилей. Выбран оптимальный метод. На основании выбора привели пример поиска решения. В дальнейшем планируется исследование, которое позволит определить реальный «вес» всех факторов, а также выбрать среду разработки данной СППР.
Важное замечание
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение – декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Попов Э.В. Экспертные системы/ Э.В.Попов. М.: Наука, 1987, с. 180 – 184.
- Нейлор К. Как построить свою экспертную систему/ К.Нейлор; пер. с англ. под ред. Н.Н. Слеповой. М.: Энергоатомиздат, 1991, с. 15 – 22.
- Черноруцкий И. Г. Методы принятия решений/Черноруцкий И. Г.: БХВ-Петербург, 2005, с. 65 – 70.
- Информационный сайт, посвящённый теме страхования [Электронный ресурс]. – Режим доступа: http://www.insur-info.ru/
- Информационный сайт, рейтингового агентства [Электронный ресурс]. – Режим доступа: http://www.raexpert.ru/
- Официальный сайт конгресса по андеррайтингу[Электронный ресурс]. – Режим доступа: http://underwriting-congress.ru/
- Архипов А.П. Андеррайтинг в страховании. Теоретический курс и практикум: учебное пособие для студентов вузов, обучающихся по специальности 08.01.05. - М.: ЮНИТИ-ДАНА, 2007г., стр. 292
- Информационный сайт, посвящённый теме страхования[Электронный ресурс]. – Режим доступа: http://insbizz.blogspot.com/
- Архипов А.П. Андеррайтинг в страховании. Теоретический курс и практикум: учебное пособие для студентов вузов, обучающихся по специальности 08.01.05. - М.: ЮНИТИ-ДАНА, 2007г., стр. 107
