Содержание

1. Введение
2. 1. Автоматическая сегментация изображений
1. 1.1 Постановка задачи
2. 1.2 Оценка качества работы методов автоматической сегментации
3. 1.3 Методы автоматической сегментации
1. 1.3.1 Кластеризация цветового пространства
2. 1.3.2 Методы выращивания регионов, дробления–слияния
3. 1.3.3 Моделирование изображения Марковским полем
4. 1.3.4 Методы, основанные на операторах выделения краев
5. 1.3.5 Методы теории графов
6. 1.3.6 Метод Normalized Cut
7. 1.3.7 Метод Nested Cuts
8. 1.3.8 Метод M. Pavan и M. Pelillo
9. 1.3.9 Метод сегментации SWA
10. 1.3.10 Оптимизационный подход
11. 1.3.11 Настройка параметров
3. 2. Интерактивная сегментация изображений
1. 2.1 Постановка задачи
2. 2.2 Оценка качества работы алгоритмов интерактивной сегментации
4. Выводы
5. Список источников

Введение

Сегментацией изображения называется разбиение изображения на непохожие по некоторому признаку области [1],[5]. Предполагается, что области соответствуют реальным объектам, или их частям, а границы областей соответствуют границам объектов. Сегментация играет важную роль в задачах обработки изображений и компьютерного зрения.

Методы сегментации можно разделить на два класса: автоматические – не требующие взаимодействия с пользователем и интерактивные – использующие пользовательский ввод непосредственно в процессе работы [2],[3].

Основной целью квалификационной работы магистра является разработка методов и алгоритмов контурной сегментации в задачах поиска однородных объектов на изображении. Для достижения этой цели необходимо:

1. провести анализ существующих методов и алгоритмов контурной сегментации изображений;
2. осуществить постановку задачи автоматической и интерактивной сегментации изображений;
3. рассмотреть основные критерии оценки качества работы методов и алгоритмов автоматической и интерактивной сегментации;
4. разработать методы и алгоритмы контурной сегментации;
5. разработать программное обеспечение для поиска однородных объектов на изображении.

1. Автоматическая сегментация изображений

1.1 Постановка задачи

Задачи автоматической сегментации делятся на два класса:

1. выделение областей изображения с известными свойствами;
2. разбиение изображения на однородные области.

Между этими двумя постановками задачи есть принципиальная разница. В первом случае задача сегментации состоит в поиске определенных областей, о которых имеется априорная информация (например, мы знаем цвет, форму областей, или интересующие нас области представляют собой изображения известного объекта). Методы этой группы узко специализированы для каждой конкретной задачи. Сегментация в такой постановке используется в основном в задачах машинного зрения (анализ сцен, поиск объектов на изображении) [4],[6],[7].

Во втором случае никакая априорная информация о свойствах областей не используется, зато на само разбиение изображения накладываются некоторые условия (например, все области должны быть однородны по цвету и текстуре). Так как при такой постановке задачи сегментации не используется априорная информация об изображенных объектах, то методы этой группы универсальны и применимы к любым изображениям. В основном сегментация в этой постановке применяется на начальном этапе решения задачи, для того чтобы получить представление изображения в более удобном виде для дальнейшей работы [8],[9].

Вначале рассмотрим постановку задачи сегментации, как разбиения изображения на однородные области. Такая постановка возникла раньше, чем задача выделения областей изображения с известными свойствами, и методы этой группы на данный момент хорошо разработаны.

Ясно, что задача разбиения изображения на однородные области поставлена некорректно, поскольку далеко не всегда для изображения есть единственно «правильная» сегментация, и далеко не всегда задача сегментации имеет единственное решение. По той же причине нет и объективного критерия оценки качества разбиения изображения.

Рисунок 1 - Исходное изображение

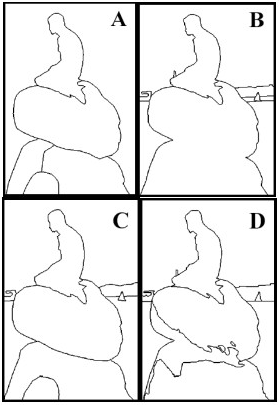Рисунок 2 - Варианты сегментации исходного изображения

1.2 Оценка качества работы методов автоматической сегментации

Поскольку сегментация обычно используется не самостоятельно, а как часть некоторой системы (например, системы машинного зрения), то с практической точки зрения, качество работы метода оценивается исходя из работы системы в целом. Поэтому один и тот же метод сегментации может оказаться хорошим для одной задачи и плохим для другой. Для грубой оценки качества метода в конкретной задаче обычно фиксируют несколько свойств, которыми должна обладать хорошая сегментация. Качество работы метода оценивается в зависимости от того, насколько полученная сегментация обладает этими свойствами. Наиболее часто используются следующие свойства:

1. однородность регионов (однородность цвета или текстуры);
2. непохожесть соседних регионов;
3. гладкость границы региона;
4. маленькое количество мелких «дырок» внутри региона.

Более общий подход к оценке качества работы метода, не учитывающий конкретного приложения, состоит в тестировании методов на общей базе изображений, для которых известна «правильная» сегментация. Например, Berkeley Segmentation Dataset насчитывает более 1000 изображений, отсегментированных вручную 30 разными людьми [2].

1.3 Методы автоматической сегментации

1.3.1 Кластеризация цветового пространства

В постановке задачи сегментации прослеживается аналогия с задачей кластеризации (или обучения без учителя). Для того чтобы свести задачу сегментации к задаче кластеризации, достаточно задать отображение точек изображения в некоторое пространство признаков и ввести метрику (меру близости) на этом пространстве признаков.

В качестве признаков точки изображения можно использовать представление ее цвета в некотором цветовом пространстве, примером метрики (меры близости) может быть евклидово расстояние между векторами в пространстве признаков. Тогда результатом кластеризации будет квантование цвета для изображения. Задав отображение в пространство признаков, можно воспользоваться любыми методами кластерного анализа. Наиболее популярные методы кластеризации, используемые для сегментации изображений – к–средних (обобщенный метод Ллойда), EM алгоритм.

Основная проблема методов кластеризации, состоит в том, что пространственное расположение точек либо не учитывается совсем, либо учитывается косвенно (например, используя координаты точки как один из признаков). Поэтому обычно после кластеризации точек изображения проводят процедуру выделения связных компонент.

Методы кластеризации плохо работают на зашумленных изображениях: часто теряют отдельные точки регионов, образуется много мелких регионов, и. т.п.

1.3.2 Методы выращивания регионов, дробления–слияния

Методы этой группы учитывают пространственное расположение точек напрямую.

Методы выращивания регионов основаны на следующей идее. Сначала по некоторому правилу выбираются центры регионов (seeds), к которым поэтапно присоединяются соседние точки, удовлетворяющих некоторому критерию. Процесс выращивания регионов (region growing) останавливается, когда ни одна точка изображения не может быть присоединена ни к одному региону.

Применяются разные критерии, на основании которых точка присоединяется или не присоединяется к региону: близость (в некотором смысле) точки к центру региона; близость к соседней точке, присоединенной к региону на предыдущем шаге; близость по некоторой статистике региона; стоимость кратчайшего пути от точки до центра региона, и т. п.

В основном процедура выращивания региона используется для получения отдельных регионов, однако, применяя эту процедуру последовательно или одновременно для нескольких регионов, можно получить разбиение всего изображения. Существуют различные стратегии выбора зерен (seeds) и выращивания регионов.

Методы дробления–слияния состоят из двух основных этапов: дробления и слияния. Дробление начинается с некоторого разбиения изображения, не обязательно на однородные области. Процесс дробления областей происходит до тех пор, пока не будет получено разбиение изображения (пересегментация), удовлетворяющее свойству однородности сегментов. Затем происходит объединение схожих соседних сегментов до тех пор, пока не будет получено разбиение изображения на однородные области максимального размера.

Конкретные методы различаются алгоритмами, используемыми на этапах дробления и слияния. Для получения пересегментации изображения используются алгоритмы k–средних, watershed, fuzzy expert systems, на втором этапе используются алгоритмы k–средних, самоорганизующиеся карты Кохонена, fuzzy expert systems, и т. д. На этапе слияния регионов используются relaxation process, k–средних, SIDE–уравнения, самоорганизующиеся карты Кохонена,и т. д.

1.3.3 Моделирование изображения Марковским полем

Хорошей моделью изображения служит Марковское случайное поле. Данная модель основана на предположении, что цвет каждой точки изображения зависит от цветов некоторого множества соседних точек. Предложено также обобщение модели изображения для случая текстурной сегментации. Данный подход является достаточно сложным в реализации, однако может являться наиболее адекватным в случае важности учёта текстуры при сегментации.

1.3.4 Методы, основанные на операторах выделения краев

При данном подходе задача сегментации формулируется как задача поиска границ регионов. Методы поиска границ хорошо разработаны для полутоновых изображений. Полутоновое изображение рассматривается как функция двух переменных (x и y), и предполагается, что границы регионов соответствуют максимумам градиента этой функции. Для их поиска применяется аппарат дифференциальной геометрии (в простейшем случае это фильтры Roberts, Kirsch, Prewitt, Sobel).

Для повышения устойчивости к шуму, перед применением фильтрации изображение обычно размывают. Благодаря коммутативности оператора Лапласа и Гауссова фильтра, можно одновременно осуществлять размытие и поиск границ. В методе Canny комбинируются результаты поиска границ при разной степени размытия.

Другой подход основан на применении steerable filters, которые осуществляют дифференцирование по направлению. Для таких фильтров можно выбрать базис, через который выражается дифференцирование по любому направлению. Для поиска границ комбинируются результаты применения базисных фильтров.

Ясно, что выбор критерия для граничных точек определяет качество работы краевых методов. Для выбора оптимального критерия граничных точек применяется машинное обучение.

Основной проблемой методов поиска границ является неустойчивость к шуму. Кроме того, поскольку понятие границы свое для каждой задачи, каждый раз при применении методов поиска границ требуется дополнительно выбирать метод доработки результатов фильтрации (edge linking, edge relaxation).

1.3.5 Методы теории графов

Методы теории графов – одно из наиболее активно развивающихся направлений в сегментации изображений.

Общая идея методов этой группы следующая. Изображение представляется в виде взвешенного графа, с вершинами в точках изображения. Вес ребра графа отражает сходство точек в некотором смысле (расстояние между точками по некоторой метрике). Разбиение изображения моделируется разрезами графа.

Обычно в методах теории графов вводится функционал «стоимости» разреза, отражающий качество полученной сегментации. Так задача разбиения изображения на однородные области сводится к оптимизационной задаче поиска разреза минимальной стоимости на графе. Такой подход позволяет помимо однородности цвета и текстуры сегментов управлять также формой сегментов, их размером, сложностью границ и т. п.

Для поиска разреза минимальной стоимости применяются различные методы: жадные алгоритмы (на каждом шаге выбирается такое ребро, чтобы суммарная стоимость разреза была минимальной), методы динамического программирования (гарантируется, что, выбирая на каждом шаге оптимальное ребро, получим в итоге оптимальный путь), алгоритм Дейкстры, и т. п. Рассмотрим некоторые методы теории графов подробнее.

1.3.6 Метод Normalized Cut

Метод Normalized Cut предложен J. Shi, J. Malik (1997). Вводится нормализованный функционал качества разреза так, чтобы одновременно максимизировать различие точек между классами и минимизировать различия точек внутри класса. Оптимизация нормализованного функционала сводится к задаче поиска собственных значений матрицы попарных расстояний между всеми точками изображения. Для сегментации изображения на две части достаточно найти второе по величине собственное значение такой матрицы.

1.3.7 Метод Nested Cuts

Метод Nested Cuts предложен Olga Veksler (2000). Основной принцип этого метода состоит в отделении каждой точки изображения от специальной точки за пределами изображения разрезом минимальной стоимости. При таком подходе изображение делится на непересекающиеся сегменты. Показано, что величиной сегментов изображения можно управлять, накладывая ограничения на стоимость разреза.

1.3.8 Метод M. Pavan и M. Pelillo

M. Pavan и M. Pelillo (2003) был предложен новый подход, основанный на разрезах графа. Авторы вводят такое определение сегмента, которое позволяет переформулировать задачу поиска разреза на графе как задачу квадратичного программирования. Предложен метод решения полученной задачи, основанный на методах эволюционной теории игр. Этот подход также требует хранения в памяти матрицы попарных расстояний, как и метод Normalized Cuts.

1.3.9 Метод сегментации SWA

Метод сегментации SWA (Segmentation by Weighted Aggregation) основан на группировании схожих точек изображения. Основная идея метода состоит в построении пирамиды взвешенных графов, каждый из которых получен из предыдущего путем объединения схожих вершин.

Качество работы методов теории графов сильно зависит от выбора метрики. Поэтому для выбора оптимальной метрики в применяют машинное обучение. Основные проблемы методов теории графов – это низкая скорость работы и большие затраты памяти. Большинство методов требует хранения в памяти матрицы попарных расстояний между точками изображения, размер которой равен квадрату числа точек. Такие ограничения делают графовые методы практически неприменимыми для больших изображений.

1.3.10 Оптимизационный подход

Задачу разбиения изображения на однородные области можно свести к задаче оптимизации. Для этого задачу сегментации формулируют как задачу поиска разбиения изображения, обладающего определенными свойствами, и затем вводится функционал, который отражает степень соответствия полученной сегментации предъявляемым требованиям. Например, в графовых методах оптимизируется функционал стоимости разреза.

1.3.11 Настройка параметров

Почти у всех описанных методов сегментации есть масса параметров, значения которых для каждой конкретной задачи приходится подбирать эвристически. Одним из подходов к решению этой проблемы является использование машинного обучения. Машинное обучение дает хороший метод избежать большого количества эвристик при выборе параметров алгоритма. Обучаемые методы сегментации – одно из наиболее перспективных на данный момент направлений.

В основе настройки параметров при помощи машинного обучения лежит следующий принцип: сначала производится настройка параметров метода сегментации на некоторой базе отсегментированных вручную изображений, и затем новые изображения сегментируются при помощи уже настроенного метода.

2. Интерактивная сегментация изображений

В последнее время стало ясно, что современные автоматические алгоритмы не способны решать произвольные задачи сегментации с гарантированным результатом [3]. Более того, по всей видимости, в ближайшее время такие алгоритмы не появятся. Поэтому всё большее и большее внимание уделяется интерактивной сегментации изображений.

Настоящий прорыв в данной области произошёл в 2000 г. – с изобретением Юрием Бойковым и Мари-Пьер Джолли алгоритма GraphCut. Этот алгоритм де-факто стал эталонным. Большая часть новых алгоритмов интерактивной сегментации изображений являются развитием алгоритма GraphCut. Остальные алгоритмы сравниваются, в первую очередь, с ним. Разрезы графов, на которые опирается GraphCut, стали активно использоваться и в других областях компьютерного зрения: сегментации видео, ститчинге, стерео-реконструкции [1],[3],[5].

Интерактивная сегментация изображений активно используется для редактирования изображений, анализа медицинских данных, а также является составной частью многих алгоритмов компьютерного зрения [10],[11],[12].

2.1 Постановка задачи

В интерактивной сегментации изображений обычно рассматривается задача разбиения только на две области – объект и фон (разбиение на большее число областей получается многократным разбиением на две области) [3].

На вход алгоритм получает:

1. исходное изображение;
2. какую–то дополнительную информацию от пользователя:
   1. ограничение на то, что некоторые конкретные пиксели обязательно должны принадлежать объекту (фону);
   2. ограничивающий прямоугольник вокруг объекта;
   3. примерную границу объекта.

В процессе работы алгоритма пользователь может уточнять или дополнять входные данные.

На выходе алгоритм должен дать разбиение исходного изображения, удовлетворяющее наложенным пользователям ограничениям. Это разбиение должно удовлетворять неким априорным представлениям пользователя о разбиении изображенных объектов.

Рисунок 3 - Пример интерактивной сегментации изображения. (анимация - 4 кадра)

2.2 Оценка качества работы алгоритмов интерактивной сегментации

В автоматической сегментации, для построения меры качества разбиения, используются предположения о том, что похожесть цвета пикселей, текстуры внутри одного объекта должна быть максимальной, а между объектами – минимальной [2]. Но в интерактивной сегментации пользователь может делать сколь угодно много подсказок алгоритму – добавлять новые ограничения, уточнять входную информацию до тех пор, пока не получит ожидаемого результата. Понятно, что в пределе, когда пользователь явно укажет про каждый пиксель, к какой области он должен принадлежать, он всегда получит идеальную сегментацию. Можно было бы оценивать качество сегментации при одних и тех же подсказках, но различные алгоритмы получают различную входную информацию от пользователя [3],[8],[9].

Также в интерактивной сегментации предполагается, что пользователь при помощи подсказок алгоритму – дополнительного ввода, должен иметь возможность отсегментировать объект даже в тех случаях, когда его часть и по цвету и по текстуре ближе фону, чем оставшейся части объекта. Это тоже затрудняет создание объективных метрик [3].

Поэтому естественно, что для сравнения алгоритмов интерактивной сегментации чаще всего используют субъективное сравнение: берется несколько изображений, и нескольким пользователям ставится одна из двух задач:

1. отсегментировать данным алгоритмом все изображения не хуже заданного уровня (сравнение на «не хуже» осуществляется субъективно самими пользователями, для сравнения даётся какой–то образец сегментации), после чего измеряется, при каком алгоритме на эту задачу ушло меньше всего времени;
2. за заданное, ограниченное время, как можно лучше отсегментировать данные изображения; после истечения положенного срока, пользователь субъективно оценивает, какой алгоритм дал лучшую сегментацию.

Выводы

В данной квалификационной работе проведен анализ методов и алгоритмов контурной сегментации изображений. В работе рассмотрены существующие подходы к автоматической и интерактивной сегментации изображений, достоинства и недостатки каждого из подходов, выделены критерии оценки качества методов и алгоритмов сегментации, а также спектр применения различных методов сегментации.

Проведенное исследование методов и алгоритмов контурной сегментации будет в дальнейшем использовано для решения задач поиска подобных изображений.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

1. Конушин А.С. Материалы курса лекций лаборатории компьютерной графики при ВМК МГУ.
   // http://courses.graphicon.ru/files/courses/vision2/2012/lectures/cv2012_14_segmentation.pdf
2. Вежневец А. Баринова О. Методы сегментации изображений: автоматическая сегментация.
   // http://cgm.computergraphics.ru/content/view/147
3. Конушин В. Вежневец В. Методы сегментации изображений: интерактивная сегментация.
   // http://cgm.computergraphics.ru/content/view/172
4. Вежневец А. Выделение связных областей в цветных и полутоновых изображениях.
   // http://cgm.computergraphics.ru/content/view/53
5. Фурман Я.А. Введение в контурный анализ. // ФИЗМАТЛИТ 2003, 592 стр.
6. Шлезингер М. И. Математические средства обработки изображений. // Наукова думка, 1989, 196 стр.
7. Шлезингер М. И. Теоретические и прикладные вопросы распознавания изображений. // Издательство института кибернетики АН УССР, 1991, 86 стр.
8. Rafael Ceferino Gonzalez, Richard Eugene Woods. Digital Image Processing. // Prentice Hall, 2008, 954 p.
9. Bernd Jähne. Digital Image Processing. // Springer, 2005, 607 p.
10. David Salomon. Data Compression. // Springer, 2007, 1092 p.
11. Paragios N., Chen Y., Faugeras O. Handbook of Mathematical Models in Computer Vision. // Springer, 2010, 605 p.
12. Francus P. Image Analysis, Sediments and Paleoenvironments. // Springer, 2004, 330 p.