Шевченко Олексій Олегович
Факультет комп'ютерних наук та технологій
Кафедра програмного забезпечення інтелектуальних систем
Спеціальність Програмне забезпечення систем
Дослідження способів оптимізації ігрового штучного інтелекту за рахунок підвищення ефективності пошуку шляху агентами
Науковий керівник: к.т.н. доц. Жук Олександр Вікторович
Реферат з теми випускної роботи
Зміст
- Введення
- 1. Актуальність теми
- 2. Методи знаходження найкоротших шляхів
- 2.1 Алгоритм Дейкстри
- 2.2 Алгоритм А *
- 2.3 Алгоритм Jump Point Search ( JPS )
- 3. Методи локальних ухилень
- 3.1 Швидкісна перешкода
- 3.2 Взаємна швидкісна перешкода
- 4. Методи побудови шляху на навігаційній поверхні
- 4.1 Переміщення по полігонах
- 4.2 Переміщення використовуючи грані полігонів
- 4.3 Переміщення по точках
- 4.4 Гібридний метод
- 4.5 Згладжування шляху
- 5. Рішення проблем використання методів швидкісних перешкод на навігаційній поверхні
- 5.1 Забезпечення навігації вздовж прокладеного маршруту і одночасний аналіз можливих колізій
- 5.2 Облік обмежень на прохідність карти при розрахунку локального ухилення
- 5.3 Повторне прокладання маршруту після виконання локального ухилення
- Висновки
- Список джерел
Введення
Теорія знаходження найкоротших шляхів має велике значення в сучасному світі. Завдяки своєму широкому застосуванню, вона останнім часом інтенсивно розвивається: поряд з удосконаленням вже існуючих методів розробляються принципово нові.
Багато завдань оптимізації пов'язані саме з пошуком найкоротших шляхів. Як результат - пошук шляху в сучасному світі використовується практично скрізь: від систем глобального позиціонування для знаходження найкоротшого маршруту серед міських вулиць і шляхів між містами, у військових і цивільних системах автопілотування, в транспортно-експедиційному обслуговуванні - і аж до комп'ютерних ігор.
Алгоритми пошуку найкоротших шляхів діляться на два типи.
- Пошук шляху на дискретній робочій поверхні (ДРП).
- Пошук шляху на графі.
Обидва класи алгоритмів мають свої переваги і недоліки, а так само свою область застосування. Перший клас алгоритмів є досить простим, але дає не завжди хороші результати, тому в даній роботі буде розглядатися другий клас.
Знаходження найкоротшого шляху це не єдина проблема. Після знаходження найкоротшого шляху в точку призначення деякого агенту необхідно пройти цей шлях так, щоб не перешкодити іншим агентам які переміщаються поруч. Для вирішення цієї проблеми так само існує ряд алгоритмів які забезпечують усім агентам безпечний шлях до точки призначення з мінімальними відхиленнями від прокладеного шляху і за мінімальний час.
1. Актуальність теми
Сучасні відеоігри – це дуже складні програми, до яких пред'являються дуже серйозні вимоги. Все, що відбувається на екрані має бути максимально реалістично, і максимально швидко. Якщо не буде бодай однієї з цих вимог, користувачам буде просто нудно.
Сьогодні існує досить багато різних алгоритмів і методик пошуку найкоротшого шляху і обходу рухомих перешкод на деякій віртуальній карті. Але всі ці методи працюють самі по собі, але не розраховані на роботу спільно, або не враховують якихось незначних особливостей. Так, наприклад, методи обходу рухомих перешкод не враховують статичні перешкоди, а методи пошуку шляху не враховують розмірів агента при прокладанні шляху.
Враховуючи все вищеперелічене, актуальним завданням є комбінування методів пошуку шляху і локальних ухилень на карті представленою навігаційною поверхнею для створення максимально реалістичної поведінки, логічного й швидкого переміщення агентів на карті.
2. Методи знаходження найкоротших шляхів
В областях теорії графів є декілька алгоритмів, які можуть шукати шляхи на поверхні зі складними перешкодами і зваженими областями. У літературі, багато з цих алгоритмів представлені в термінах зміни станів або проходу по вузлах графа. Це часто використовується для вирішення багатьох проблем, включаючи п'ятнашки
і кубик Рубіка, де станом є поєднання цифр або кубиків, і сусідні стани (або суміжні вузли) відвідуються шляхом переміщення цифр або повороту граней кубика. Застосування цих алгоритмів до пошуку шляху в геометричному просторі вимагає простої адаптації: стан або вузол графа представляють об'єкт, що знаходиться в певній клітці, і пересування в сусідні клітини відповідає переміщенню в сусідні стани або суміжні вузли.
Далі йде опис алгоритмів пошуку шляху, від простих до більш складних.
2.1 Алгоритм Дейкстри
Е. Дейкстра розробив класичний алгоритм для проходу по графах, грані яких мають різну вагу. На кожному кроці, він шукає необроблені вузли близькі до стартового, потім переглядає сусідів знайденого вузла, і встановлює або оновлює їх відповідні відстані від старту. Цей алгоритм бере до уваги вартість або довжину шляху і оновлює вузли, якщо до них знайдений кращий шлях. На рисунку 1 показана хороша адаптація алгоритму до вартості місцевості. Однак, він має слабкість пошуку в ширину, ігноруючи напрямок до мети.
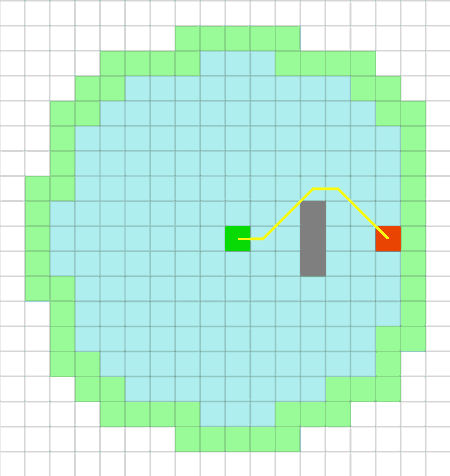
Рисунок 1 - Алгоритм Дейсктри
2.2 Алгоритм А *
Найкращим алгоритмом для пошуку оптимальних шляхів у різних просторах є A* (читається як А - зірочка
). Цей евристичний пошук сортує всі вузли по наближенню найкращого маршруту, що проходить через цей вузол. Типова формула евристики виражається у вигляді:
f(n) = g(n) + h(n),
де :
- f(n) - значення оцінки, призначене вузлу n;
- g(n) - найменша вартість прибуття в вузол n з точки старту;
- h(n) - евристичне наближення вартості шляху до мети від вузла n.
A* має багато цікавих властивостей. Він гарантовано знаходить найкоротший шлях, доти поки евристичне наближення h(n) є допустимим, тобто він ніколи не перевищує дійсного відстані що залишилась до цілі. Цей алгоритм найкращим чином використовує евристику: жоден інший алгоритм не розкриє менше число вузлів, не враховуючи вузлів з однаковою вартістю. На рисунку 2 показано як A* справляється з ситуацією проблемною для інших алгоритмів.
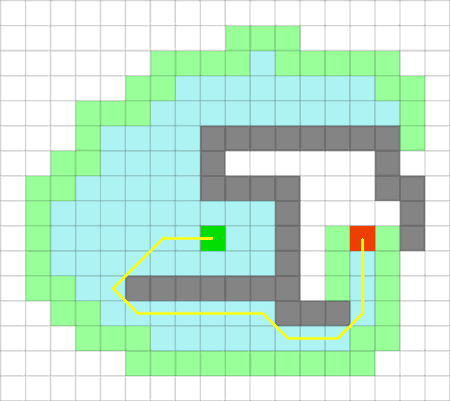
Рисунок 2 - Алгоритм А* у складній ситуації
2.3 Алгоритм Jump Point Search (JPS)
Цей алгоритм є поліпшеним алгоритмом пошуку шляху A*. JPS прискорює пошук шляху, перестрибуючи
багато місць, які повинні бути переглянуті. На відміну від подібних алгоритмів JPS не вимагає попередньої обробки і додаткових витрат пам'яті.
Алгоритм працює на неорієнтованому графі єдиної вартості. Кожне поле карти має максимум 8 сусідів, які можуть бути прохідні або ж ні. Кожен крок у напрямку (по вертикалі або по горизонталі) має вартість 1; крок по діагоналі має вартість sqrt(2). Рухи через перешкоди заборонені. Позначення відноситься до одного з восьми напрямків руху (вгору, вниз, вліво і т.д.).
Стрибкові точки
дозволяють прискорити алгоритм пошуку шляху, розглядаючи тільки необхідні
точки. Такі точки можуть бути описані двома простими правилами вибору сусідів при рекурсивному пошуку: одне правило для прямолінійного руху й інше - для діагонального. В обох випадках необхідно довести, що виключаючи з набору найближчих сусідів навколо точки, знайдеться оптимальний шлях з предка поточної точки до кожного з сусідів, і цей шлях не буде містити в собі відвідану точку. Приклад роботи алгоритму показаний на рисунку 3.
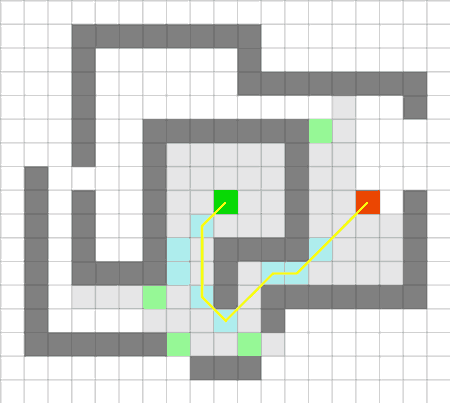
Рисунок 3 - Приклад роботи JPS
3. Методи локальних ухилень
На відміну від пошуку шляху, обхід перешкод є динамічним завданням, тобто вимагає розрахунку вектора швидкості агентів в кожен момент часу t.
Існує кілька різних підходів до вирішення цього завдання. Найпростіший підхід - це поведінки керування (Steering Behaviors). Цей підхід включає в себе багато різних методик керування автономним агентом. Наприклад, переслідування, ухилення, трасування шляху, рух групою. Різні поведінки агента показані на рисунку 4.
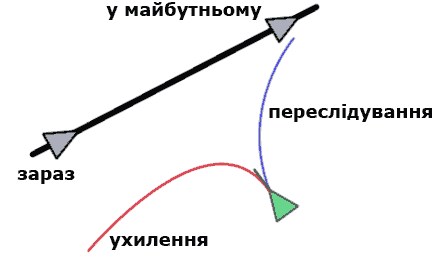
Рисунок 4 - Поведінки управління
Для вирішення завдання обходу рухомих перешкод необхідно скомбінувати переслідування, ухилення і трасування шляху.
3.1 Швидкісна перешкода
Швидкісна перешкода для віртуального агента, створена рухомою перешкодою - це всі вектори швидкостей при русі по яким, через невеликий проміжок часу, відбудеться колізія між агентом і рухомою перешкодою, за умови що перешкода буде рухатися з постійною швидкістю. Це означає, що якщо агент вибере собі вектор швидкості, який знаходиться в області швидкісної перешкоди, то, в майбутньому, між агентом і перешкодою відбудеться колізія. Якщо швидкість буде обрана за межами швидкісної перешкоди - колізія не відбудеться. Геометричне уявлення швидкісної перешкоди VOab для агента А по відношенню до агента B, що відповідає конусу, показано на рисунку 5.
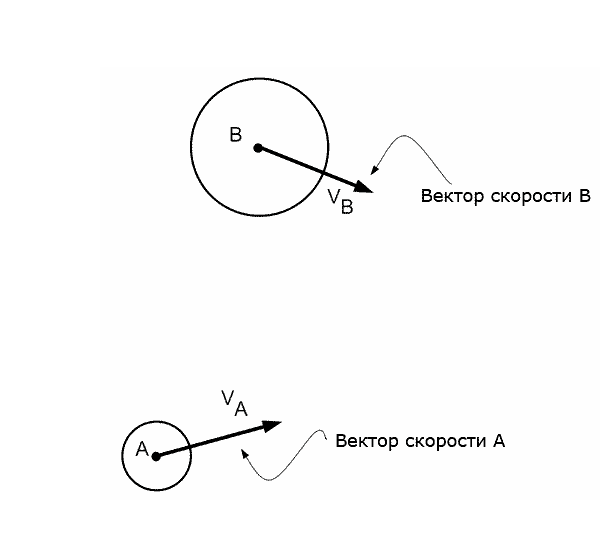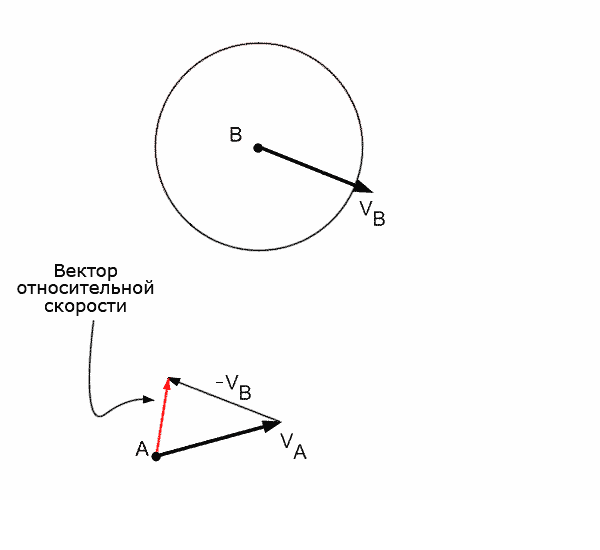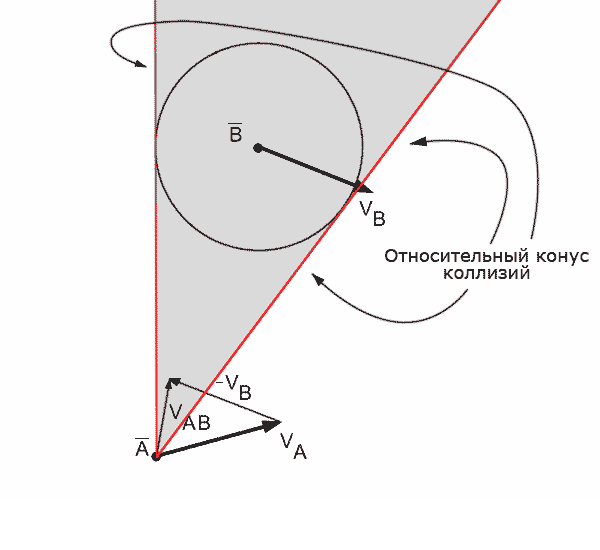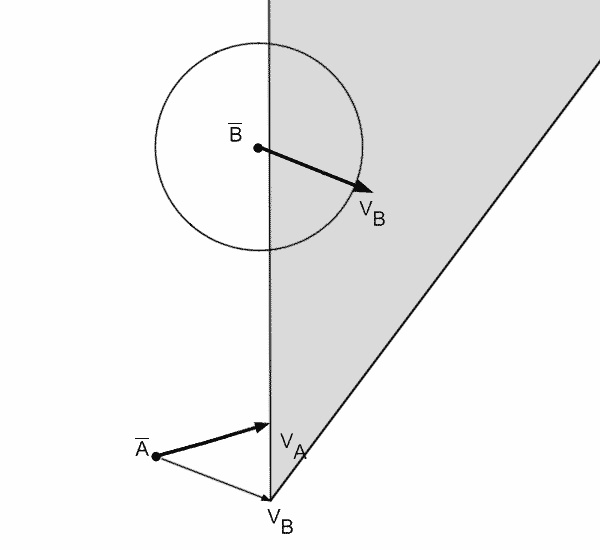
Рисунок 5 - Приклад побудови швидкісної перешкоди для агента А по відношенню до агента В (анімація: об'єм - 93,9 КБ, кількість кадрів - 22, розмір - 600х550)
Цей метод добре працює коли є один віртуальний агент який рухається в просторі з великою кількістю рухомих перешкод. Але, на жаль, цей метод погано працює на групі рухомих агентів, де кожен агент активно змінює свій вектор швидкості, для того, щоб уникнути колізії, тому що припускає, що інші агенти не будуть змінювати свою швидкість. Це створює коливання в русі всіх агентів.
3.2 Взаємна швидкісна перешкода
Взаємна швидкісна перешкода спрямована на вирішення проблеми коливань, що виникають при використанні швидкісної перешкоди, шляхом дозволу агентам реагувати на зміну вектора швидкості іншими агентами. Замість того, що б один з агентів брав на себе всю відповідальність за вчинення маневру ухилення, взаємна швидкісна перешкода, дозволяє агенту здійснити лише половину, допускаючи що другу половину здійснить інший агент. Геометричне уявлення взаємного швидкісного перешкоди RVOab для віртуального агента А по відношенню до агента B, відповідне швидкісній перешкоді з переміщеною вершиною, показано на рисунку 6.
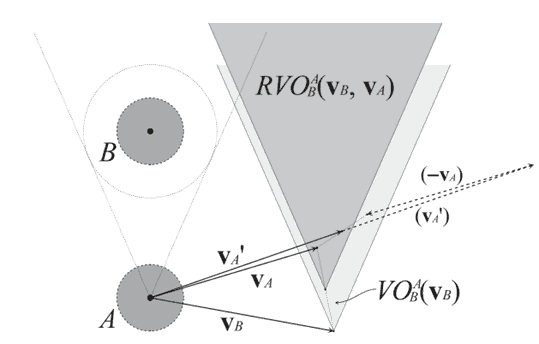
Рисунок 6 - Взаємна швидкісна перешкода
Але і цей метод не ідеальний. У нього є ряд проблем, найбільш значимою з яких є проблема взаємних танців
. Вона проявляє себе тоді, коли агенти сильно відхиляються від наміченої тректоріі руху, внаслідок чого можуть виявитися заблокованими іншими агентами. На вирішення цієї проблеми направлені метод оптимальних взаємних швидкісних перешкод і метод гібридних взаємних швидкісних перешкод.
4. Методи побудови шляху на навігаційній поверхні
Навігаційна поверхня - весь прохідний простір, що складається з полігонів, що не пересікаються. Навігаційна поверхня може містити додаткову інформацію. Наприклад: вартість проходу, або умови проходу для певних класів юнітів. Будувати шляхи по ній можна використовуючи центри полігонів, грані, точки полігонів, або кілька цих методів одночасно.
4.1 Переміщення по полігонах
Кожен центр полігону являє собою вершину для графа пошуку шляху. На рисунку 7 показана навігаційна поверхня з початковою і кінцевою точкою шляху.
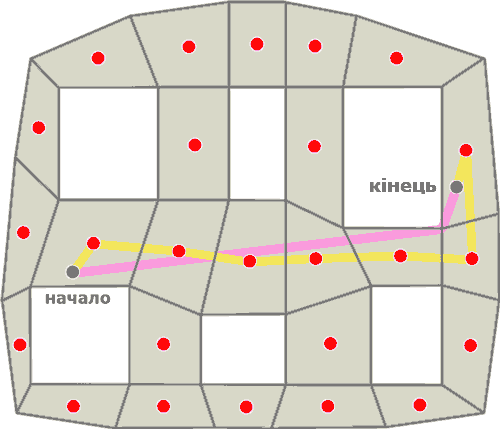
Рисунок 7 - Шлях прокладений по центрам полігонів
Жовта лінія - шлях прокладений по центрам полігонів. Рожева - найкоротший шлях. Цей підхід дає далеко не самий короткий шлях, але він один з найпростіших.
4.2 Переміщення використовуючи грані полігонів
Переміщення в центр полігону найчастіше не потрібно. Тому цей підхід дає набагато кращий результат. На рисунку 8 показаний приклад. У якості точок для переміщення обрані центри граней. Але це не обов'язково. Можна використовувати декілька точок на грані. Цей підхід дає більш точний результат ніж попередній, але шлях все ще не найкоротший.
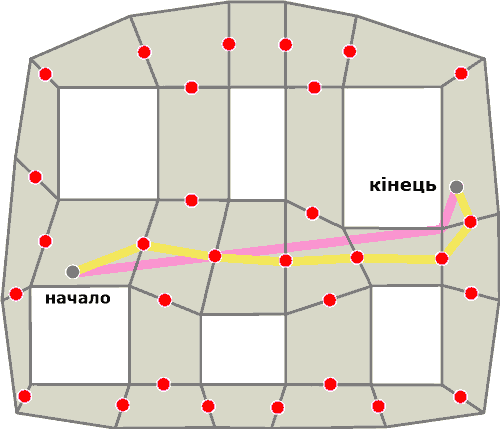
Рисунок 8 - Шлях прокладений по центрам граней полігонів
4.3 Переміщення по точках
Найкоротший шлях навколо перешкоди - це її огинання. Цей принцип використовується в даному методі. На риснку 9 показано шлях побудований по точках полігонів.
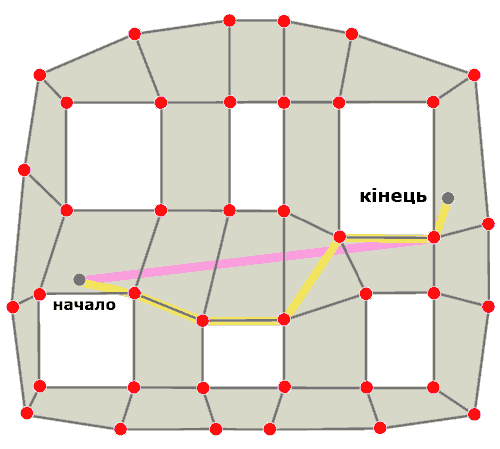
Рисунок 9 - Шлях прокладений по точках поверхні
Як видно з малюнка. На шляху з початкової точки в кінцеву є всього одна перешкода. Цей метод добре обігнув її, але рух вперед виглядає не натурально і схожий більше на рух уздовж стіни в лабіринті.
4.4 Гібридний метод
Вибір методу побудови шляху на навігаційній поверхні обмежений лише фантазією. Тому ніхто не забороняє використовувати відразу декілька методів. Наприклад на рисунку 10 показано шлях побудований за допомогою використання центрів граней і точок полігонів.
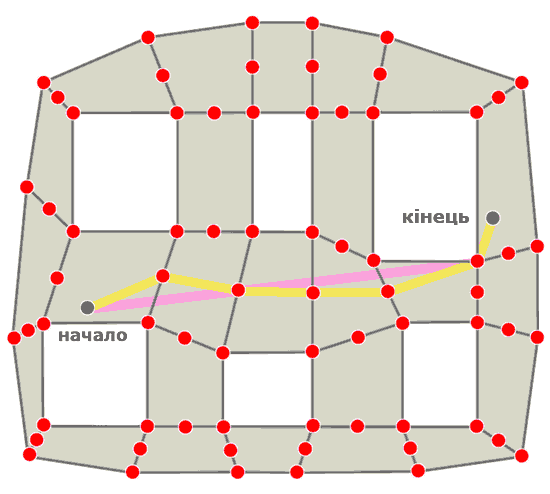
Рисунок 10 - Шлях прокладений по точках і центрах граней полігонів
Це дозволило і ефективно обігнути перешкоду і досить природно рухатися вперед.
4.5 Згладжування шляху
Всі вищеописані методи дають непоганий результат, але він все одно не є найкоротшим. Згладжування дозволяє уникнути непотрібних маневрів і рухатися прямо до мети.
Метод простий: Якщо з навігаційною точки i в точку i + 2 існує прямий шлях, то видалити точку i + 1. Повторювати це поки не залишиться точок які можна видалити.
Цей простий метод дозволить залишити тільки ті навігаційні точки, які огинають перешкоди. І якщо використовувати згладжування шляху, то для початкової побудови шляху немає необхідності використовувати центри полігонів або грані. Досить використовувати точки полігонів.
5. Рішення проблем використання методів швидкісних обмежень на навігаційній поверхні
5.1 Забезпечення навігації вздовж прокладеного маршруту і одночасний аналіз можливих колізій
Нехай найкоротший маршрут довжиною N представляє собою послідовність точок:
 , (1)
, (1)
де - початкова точка маршруту,
- початкова точка маршруту,
 - проміжні точки маршруту,
- проміжні точки маршруту,
 - кінцева точка маршруту.
- кінцева точка маршруту.
При переміщенні за маршрутом агент в кожен момент часу повинен рухатися зі швидкістю:
 , (2)
, (2)
де i - індекс останньої пройденої агентом точки маршруту,
 - величина швидкості руху агента,
- величина швидкості руху агента,
 - операція нормування вектора.
- операція нормування вектора.
Метод взаємних швидкісних перешкод не враховує дані про пункт призначення руху агента. Вхідними даними є:
- необхідний вектор швидкості для кожного з агентів (
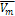 );
); - поточний вектор швидкості кожного з агентів (
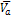 ).
).
Результатом застосування методу є новий поточний вектор швидкості для кожного з агентів. Очевидно, що для продовження руху за наміченим маршрутом, необхідний вектор швидкості  необхідно перераховувати в кожен момент часу:
необхідно перераховувати в кожен момент часу:
 , (3)
, (3)
де - поточна позиція агента на карті.
- поточна позиція агента на карті.
Описана ситуація з векторами швидкостей наведена на риcунку 11.
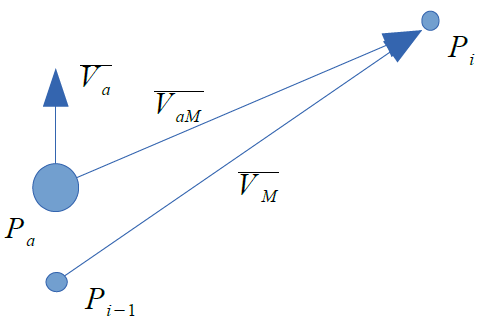
Рисунок 11 - Розрахунок вектора швидкості руху агента при спільному використанні методів пошуку найкоротшого шляху і методу взаємних швидкісних обмежень для навігації по карті
5.2 Облік обмежень на прохідність карти при розрахунку локального ухилення
Маршрут M прокладається таким чином, що агент, який рухається по ньому, може торкатися перешкод, але траєкторія його руху завжди знаходиться в межах прохідною області карти.
Водночас, при виконанні локального ухилення напрямок руху може бути обраний таким чином, що після виконання маневру агент вийде за межі області прохідності.
Метод взаємних швидкісних перешкод дозволяє розрахувати для агента вектор швидкості, що гарантує відсутність зіткнень з перешкодами. Таким чином, якщо уявити межі областей прохідності на карті як перешкоди для методу взаємних швидкісних перешкод, то розглянута проблема буде вирішена.
Кожен з полігонів навігаційної поверхні можна розбити на непересічні трикутники так, що їх сумарна площа буде дорівнювати площі полігону. Розбиття всіх полігонів навігаційної поверхні на трикутники будемо називати тріангуляцією навігаційної поверхні. Приклад навігаційної поверхні і її тріангуляції представлені на риcунку 12.
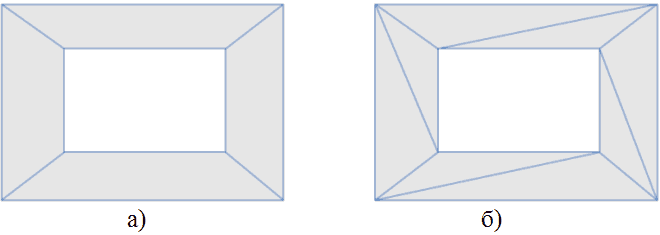
Рисунок 12 - Навігаційна поверхня (а) та її тріангуляція (б). Зафарбовані області відповідають прохідним ділянкам картки
Кожен з K отриманих трикутників являє собою повний граф. Якщо всі ці трикутники об'єднати в один граф, то отримаємо граф, що складається K компонент зв'язності. Якщо в цьому графі об'єднати вершини, що мають однакові координати, то отримаємо зв'язний граф із кратними ребрами. Нехай в отриманому графі K вершин і нехай M - матриця суміжності цього графа. Якщо над матрицею M виконати наступну операцію
 , (4)
, (4)
то це буде відповідати видаленню в отриманому графі всіх кратних ребер. Отриманий граф буде містити тільки компоненти зв'язності, кожна з яких буде циклом - контуром однієї з меж непрохідних областей на карті.
5.3 Повторне прокладання маршруту після виконання локального ухилення
Однією з властивостей маршруту, прокладеного по навігаційної поверхні, є те, що кожні дві сусідні точки в ньому знаходяться в прямій видимості одна від одної, тобто в контурах меж немає ребра, яке перетнув би відрізок  .
.
Як обговорювалося раніше, після виконання локального ухилення вектор швидкості агента до наступної точки шляху потребуватиме перерахунку. Однак не виключено, що після ухилення в контурах меж знайдеться ребро, з яким перетнеться відрізок  . Наявність такого відрізка будемо вважати показником необхідності повторного розрахунку маршруту з точки
. Наявність такого відрізка будемо вважати показником необхідності повторного розрахунку маршруту з точки  в точку E.
в точку E.
Висновки
Магістерська робота присвячена рішенню актуальної наукової задачі об'єднання методів пошуку шляху і локальних ухилень на навігаційній поверхні. У рамках проведених досліджень виконані наступні роботи:
- Проведено аналіз вже існуючих методів пошуку шляху і локальних ухилень.
- Для обраних методів і алгоритмів переглянуті можливості їх спільного використання для вирішення поставленого завдання.
- Проведено ряд тестів і виявлено основні проблеми використання методів локальних ухилень на навігаційній поверхні.
- Запропоновані можливості вирішення знайдених проблем. Реалізація цих рішень дозволить застосовувати метод взаємних швидкісних перешкод для забезпечення локальних ухилень агентів при проходженні по маршруту по карті, представленої навігаційною поверхнею.
Подальші дослідження спрямовані на наступні аспекти:
- Додавання пріоритетів агентів в методи локального ухилення.
- Врахування розмірів агента при прокладанні маршруту по навігаційної поверхні.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2014 року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Список джерел
- Алгоритм Дейкстры [Электронный ресурс] - Режим доступа: http://ru.wikipedia.org/wiki/Алгоритм_Дейкстры
- Алгоритм A* для новичков [Электронный ресурс] - Режим доступа: http://www.policyalmanac.org/games/aStarTutorial_rus.htm
- Harabor, D., Grastien, A.: Online Graph Pruning for Pathfinding on Grid Maps. In: Proceedings of the 25th National Conference on Artificial Intelligence (AAAI), San Francisco, USA (2011).
- C.W. Reynolds: Steering behaviors for autonomous characters - Game developers conference, 1999.
- P. Fiorini and Z. Shiller,
Motion planning in dynamic environments using velocity obstacles
, Int. Journal of Robotics Research, vol. 17, no. 7, pp. 760-772, 1998. - van den Berg, J., Lin, M., Manocha, D.: Reciprocal Velocity Obstacles for real-time multi-agent navigation. In: IEEE Int. Conf. on Robotics and Automation, pp. 1928–1935 (2008).
- J. Snape , J. van den Berg , S. J. Guy , D. Manocha, The Hybrid Reciprocal Velocity Obstacle, IEEE Transactions on Robotics, v.27 n.4, p. 696-706, August 2011.
- van den Berg, J., Guy, S., Lin, M., Manocha, D. (2011). Reciprocal n-body collision avoidance. In C. Pradalier, R. Siegwart, G. Hirzinger (Eds.), Robotics Research: The 14th International Symposium ISRR (pp. 3-19). Berlin, Germany: Springer.
- Marcelo Kallmann, Shortest paths with arbitrary clearance from navigation meshes, Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, July 02-04, 2010, Madrid, Spain.
