Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования
- 3. Автоматная модель
- 4. Задача анализа поведения конечных автоматов
- 5. Формальная постановка задачи
- 6. Полученные теоретические результаты
- Выводы
- Список источников
Введение
Модель конечного автомата широко используется для описания разнообразных дискретных систем и процессов. Эти системы могут подвергаться внешним искажающим воздействиям, и, как результат, изменять своё поведение. Во многих случаях такие воздействия носят локальный характер и могут быть описаны системой локальных преобразований над дугами исходного автомата–эталона. В связи с этим возникает задача сравнительного анализа поведения исходного и преобразованного автоматов и вычисления близости этих автоматов по поведению. В настоящей работе исследуется влияние одной переброски на поведение инициального определенно–диагностируемого порядка k эталона с точки зрения определения степени близости его поведения до и после переброски.
1. Актуальность темы
Теоретическое и практическое значение моделей автоматов в исследовании процессов формирования и передачи сигналов в сложных системах, решении задач технического диагностирования и проектирования стало причиной интенсивных исследований теории автоматов как математической модели сложных систем. В настоящее время практически в любой сфере человеческой деятельности встречается понятие система
. Модель конечного автомата являются одной из наиболее простых математических моделей сложных систем.
Автоматы широко используются в различных областях защиты информации. В частности, они естественным образом предоставляют возможность описывать потоковые алгоритмы шифрования. В связи с этим исследование модели конечного автомата является актуальным, а, следовательно, и изучение поведения автомата.
2. Цель и задачи исследования
Объект исследования: поведение конечного приведенного инициального автомата.
Предмет исследования:нахождение длины кратчайшего входного слова, различающего исходный автомат–эталон и автомат, полученный в результате перебросок некоторых дуг в графе переходов исходного автомата.
Целью выпускной работы магистра является разработка метода анализа автоматов, порождаемых локальными преобразованиями эталона.
Основные задачи исследования:
- Провести сравнительный анализ поведения ОД–k–эталона и автоматов, порождаемых его локальными преобразованиями.
- Поиск меры близости поведения эталона, являющегося инициальным ОД–k–автоматом, и автомата, полученного из эталона переброской одной дуги.
- Для любой переброски дуги оценить меру близости.
- Пусть К (А) – класс автоматов локально порожденных из эталона А. Задача состоит в том, чтобы описать структуру этого класса с точки зрения разбиения его на подклассы автоматов, эквивалентных по степени близости их поведения поведению эталона.
3. Автоматная модель
Сравнение поведения автоматов, получаемых в результате перебросок дуг, начнём с частного случая: в качестве эталона будем рассматривать определенно диагностируемый порядка k автомат, а под переброской будем понимать переброску ровно одной дуги.
Под моделью автомата будем понимать инициальный приведенный определенно–диагностируемый порядка k (ОД–k) автомат Мили A = (S, X, Y, δ, λ, s0), где S, X, Y – конечные множества состояний, входных и выходных символов соответственно, δ, λ − функции переходов и выходов, а s0 – начальное состояние. При необходимости, чтобы не возникало путаницы, к обозначениям этих объектов добавлен индекс А или значок штриха.
Автомат А называется инициальным, если в множестве его состояний выделено некоторое состояние s0, которое называется начальным. При функционировании инициального автомата считается, что в начальный момент времени (перед подачей на его вход некоторого слова) автомат находится в начальном состоянии s0.
В автомате А функции δ и λ обычным образом распространяются на множество всех входных слов конечной длины. Напомним, что автомат А называется ОД–k–автоматом, если k≥1 – наименьшее целое такое, что для любого входного слова p длины k и любой пары различных состояний s∈S выполняется неравенство λ(s,p) ≠ λ′(t,p), т.е. по любому порождаемому автоматом вход–выходному слову длины k однозначно определяется начальное состояние автомата.
Пусть вход–выходное слово w=(p,q) порождается состоянием s автомата А, если λ(s,р)=q. Длину слова w обозначим |w|. Два состояния s и t одного и того же автомата A или двух разных автоматов A и B соответственно, называются эквивалентными, если для всякого входного слова р′∈X* выполняется λ(a,p)=λ′(b,p), где λ′ − функция выходов автомата A или B. Автомат называется приведенным, если все его состояния попарно неэквивалентны. Каждому состоянию s поставим в соответствие множество λs всех вход–выходных слов, порождаемых этим состоянием. Под поведением автомата А будем понимать множество λs0 вход–выходных слов, порождаемых его начальным состоянием.
Автомат удобно задавать в виде графа переходов, вершины которого соответствуют состояниям из S, а дугами являются четверки (s,x,y,t), где t=δ(s,x), y=λ(s,x). Пара (x,y) называется отметкой дуги, s – ее началом, а t – концом. Если e=(t,x,y,u) – дуга в графе переходов автомата A, то переброской этой дуги из состояния u в состояние v, отличное от u, называем замену её дугой (t,x,y,v).
4. Задача анализа поведения конечных автоматов
Автоматы, близкие по поведению в том или ином смысле, исследуются достаточно давно, как и структура их классов [1]. Главным образом эта задача рассматривалась в рамках теории экспериментов с автоматами [2].
Муром было положено основание теории экспериментов с автоматами. Его исследования затрагивали два взаимосвязанных аспекта: неотличимость автоматов никакими кратными и никакими простыми (однократными) экспериментами; распознавание автоматов и их состояний с помощью таких экспериментов. Становление теории экспериментов тесно связано с работами A.M. Богомолова и его учеников, М.П. Василевского, А. Гилла, В.Н. Носкова, Н.В. Евтушенко, А.Ф. Петренко, И.К. Рысцова, В. А. Твердохлебова, С.В. Яблонского, Ф. Хенни, П. Штарке и многих других. Эти исследования разделены на три этапа: комбинаторный, сложностной и характеризационный.
Комбинаторный этап касался построения средств анализа автоматов и алгоритмов проведения экспериментов с ними, исходя из комбинаторно–мощностных соображений. Методы и результаты этого этапа достаточно полно представлены в известной книге А. Гилла [3].
На сложностном этапе основное внимание уделяется построению оптимальных по сложности алгоритмов и нахождению сложности проведения экспериментов, а также оптимальных по сложности методов анализа поведения автомата. Это потребовало анализа структуры экспериментов. Этот этап инициирован работами Ф. Хенни и М.П. Василевского, которые проводили построение контрольных экспериментов путем помещения во входные последовательности специальных подпоследовательностей (диагностических, установочных, локализующих, характеристических и т. п.), по реакции на которые исследуемого автомата можно идентифицировать его внутренние состояния. На этом этапе исследовались различные виды таких последовательностей и способы их размещения в эксперименте. Методы и результаты второго этапа достаточно полно представлены в книге В.Б. Кудрявцева, С.В. Алешина, А.С. Подколзина [4]. И.С. Грунский, по–видимому, первым назвал эти последовательности и реакции на них идентификаторами состояний, начал их систематическое изучение и обратил внимание на существование идентификаторов других ненаблюдаемых компонент поведения (например, входных последовательностей [5]). На втором этапе получено большое количество частных способов построения контрольных и распознающих экспериментов для случаев, когда они заведомо существуют. Неисследованными остались условия существования и структура таких экспериментов в общем случае. Очень трудным оказался вопрос: что должно присутствовать в этих экспериментах, а что является издержками алгоритмов их построения, то есть вопрос характеризации вышеуказанных экспериментов. Появление первых характеризационных теорем [6] можно отнести уже к становлению третьего, характеризационного, этапа.
Теория экспериментов интенсивно развивается, в ней получен ряд важных и принципиальных результатов связанных с анализом поведения автоматов. Влияние перебросок дуг на поведение автомата изучалось в [7–11], исследуя данные работы, стало известно:
- Переброска только одной дуги в приведенном автомате всегда вызывает изменение поведения – автомат становится неэквивалентным исходному приведенному автомату.
- Переброска одной дуги всегда приводит к неизоморфному автомату.
- Переброска двух дуг может привести к автомату, эквивалентному исходному.
- Для любого натурального k > 1 существует приведенный автомат, в котором найдется подмножество из k дуг, одновременная переброска которых приводит к изоморфному автомату.
- При переброске двух дуг входные–выходные отметки на перебрасываемых дугах должны совпадать.
- Возможны переброски более двух дуг, при которых входные–выходные отметки на перебрасываемых дугах различны.
- Доказаны достаточные условия изоморфизма автоматов при переброске двух дуг.
- Представлена структура автоматов, в которых возможна переброска любого числа дуг ≥ 2. Эти автоматы не являются сильно связными.
- Переброска дуг, сохраняющая изоморфизм, возможна в автоматах, обладающих определенной симметрией графа переходов, которая отражается и в циклической структуре графа.
- Существуют примеры сильно связных автоматов, в которых существует ≥ 4–х перебросок, сохраняющих изоморфизм.
5. Формальная постановка задачи
Основные понятия теории автоматов можно найти в [12].
Пусть автомат A′ получен из автомата A произвольной переброской одной дуги. Будем для определённости считать, что в результате переброски произошла замена дуги (t,x,y,u) на дугу (t,x,y,v), где t,u,v′S, u≠v. Состояния автомата A′ будем помечать штрихом так, что переброшенная дуга в нём имеет вид e′ = (t′, x, y, v′). Полученный автомат A′ назовём автоматом, локально порождённым из эталона А. Обозначим через K(А) класс всех автоматов, локально порождённых из автомата А, включая сам эталон. Интерес представляют следующие вопросы: 1) как определить степень близости поведения автоматов А и A′; 2) насколько изменилось поведение автомата после переброски дуги; 3) какова структура класса К(А) с точки зрения разбиения его на подклассы автоматов, эквивалентных по степени близости их поведения поведению эталону.
Формализуем поставленную задачу. Введем на классе автоматов бэровскую метрику [7] следующим образом. Пусть i – длина некоторого кратчайшего входного слова р, различающего начальные состояния s0 и s′0 автоматов А и A′, т.е. слова, для которого λ(s0, р) ≠ λ′ (s′0, р). Тогда положим:
![]()
Ясно, что, чем длиннее различающее слово р, тем меньше расстояние между А и A′. Пусть |X|=m и |S|=n. Каждая дуга заканчивается в одном из n состояний, и, следовательно, её можно перебросить в одно из оставшихся (n-1) состояний. Так как число дуг равно mn, то количество возможных перебросок равно mn(n-1), и, значит, класс К(А) состоит из (mn(n-1)+1) автоматов, включая эталон. Данный класс разбивается на подклассы Ki(A) автоматов, находящихся на одинаковом расстоянии 1/i от эталона. По определению, ρ(A, A′)=0, и тогда K0(A)={A}. Известно [13], что переброска одной дуги всегда приводит к неизоморфному автомату. Поэтому начальные состояния (s0, s′0) автоматов А и A′ всегда различимы некоторым словом, и, значит, ρ(A, A′)>0. Заметим, что при переброске дуги её отметка не изменяется, т.е. состояния s0 и s′0 выдают одну и ту же реакцию на каждый входной символ. Следовательно, длина различающего их слова больше или равна 2, откуда ρ(A, A′)≤1/2 и К1(А)=∅. С другой стороны, пара состояний (s0, s′0) всегда различима некоторым входным словом длины, не превосходящей (2n-1), поэтому ρ(A, A′)≥(2n-1). Таким образом: 1/(2n-1)≤ρ(A, A′)≤1/2. Итак, для класса К(А) существует разбиение на подклассы:
![]()
6. Полученные теоретические результаты
Теорема 1. Пусть А – инициальный приведенный ОД–k–автомат и A′ получен из А переброской дуги (t,x,y,u) в состояние v. Тогда ρ(A, A′)≤1/(d+k+1), где d – длина кратчайшего входного слова w такого, что δ(s0,w)=t.
Доказательство. Чтобы отличать состояния автомата А от состояний A′, будем состояния последнего помечать штрихом и пару (s,s′) называть двойственными, где s=S, s′=S′. Покажем сначала, что состояния u и v′ различимы некоторым словом длины, не большей k. Для этого воспользуемся приёмом, использованным при доказательстве того факта, что переброска дуги в любом приведенном автомате всегда приводит к автомату, не изоморфному исходному [7]. Построим автомат В, равный прямой сумме автоматов А и А′, и рассмотрим процесс построения Рk–таблиц [3] для автомата В.
Поскольку таблицы выходов автоматов А и А′ совпадают, то в таблице Р1 каждый класс эквивалентности состоит из пар двойственных состояний. Заметим, что любая пара (s, s′), кроме пары (t, t′), по любому х опять переходит в пару двойственных состояний. Пара (t, t′) – единственная, для которой это не выполняется, так как δB(t, x)=u и δB(t′, x)=v′. Отсюда следует, что пока состояния (t,t′) k–эквивалентны, любая пара (s,s′), отличная от (t,t′), будет (k+1)–эквивалентной. Сама же пара (t,t′) k–эквивалентна, пока пара (u,v′) является (k-1)–эквивалентной. Но, если (u,v′) (k-1)–эквивалентна, то тогда пары (t,t′), (u,u′), (v,v′) k–эквивалентны и, значит, состояния u,u′,v,v′ принадлежат одному классу эквивалентности в таблице Рk. Так как А ОД–k–автомат, то для некоторого i<k состояния u и v будут (i-1)–эквивалентны, но i–различимы. И тогда i–различимыми будут и состояния u и v′, где i≤k.
Пусть теперь w − кратчайшее входное слово в автомате А, переводящее его из начального состояния в состояние t, и р – кратчайшее слово, различающее u и v′. Пусть |w|=d, |p|=i, и как показано выше, i≤k. Ясно, что в автомате А′ δ(s′0,w)=t′. Тогда δ(s0,wx)=u, δ(s′0,wx)=v′, λ(s0,wx)=λ(s′0,wx), но λ(s0,wxp)≠λ(s′0,wxp), причём |wxp|≤d+1+k, что и требовалось доказать.
Покажем, что полученная оценка расстояния достижима.
На рисунке 1 приведен инициальный автономный автомат А. Пусть автомат А′ является результатом переброски одной дуги в автомате А: дуга (6,0,2,5) перебрасывается в состояние 3 и заменяется дугой (6′,0,2,3′). Поскольку перебрасывается дуга, исходящая из состояния 6, то кратчайшее слово w имеет длину d=3. Легко видеть, что λ(s0,0000)=λ(s′0,0000), но λ(s0,00000)≠λ(s′0,00000). Поэтому p=00000 и |p|=5. Отсюда ρ(A, A′)=1/5. На примере видно, что в результате переброски дуги автомат A′ стал приведенным автоматом, так как состояния 5 и 6 стали эквивалентными.
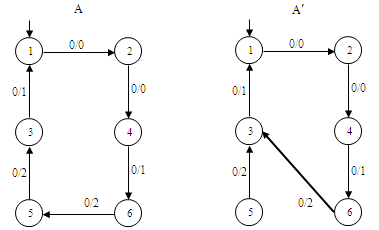
Рисунок 1 – Пример переброски одной дуги в автомате ОД–2
Теперь рассмотрим ОД–3–автомат B (рис. 2). Пусть автомат B′ является результатом переброски одной дуги в автомате B: дуга (5,1,0,2) перебрасывается в состояние 4 и заменяется дугой (5′,1,0,4′). Поскольку перебрасывается дуга, исходящая из состояния 5, то кратчайшее слово w имеет длину d=3. Легко видеть, что λ(s0,0001)=λ(s′0,0001), но λ(s0,00011)≠λ(s′0,00011). Поэтому p=00011 и |p|=5. Отсюда ρ(B, B′)=1/5. На примере видно, что в результате переброски дуги автомат B′ остался ОД–3.
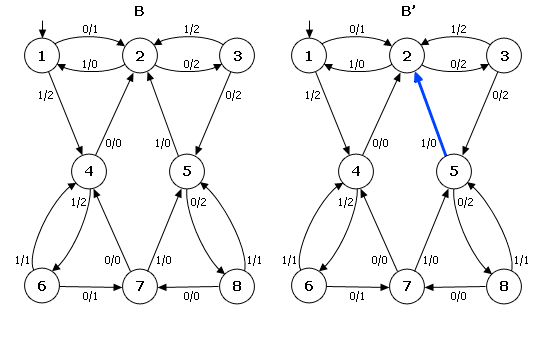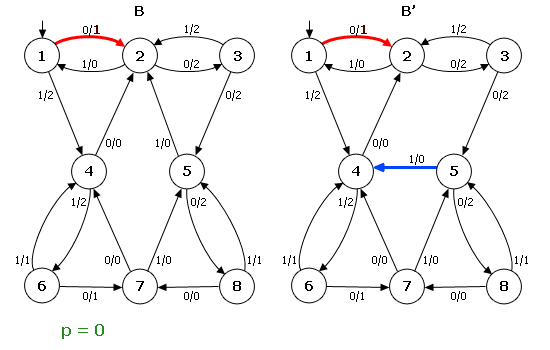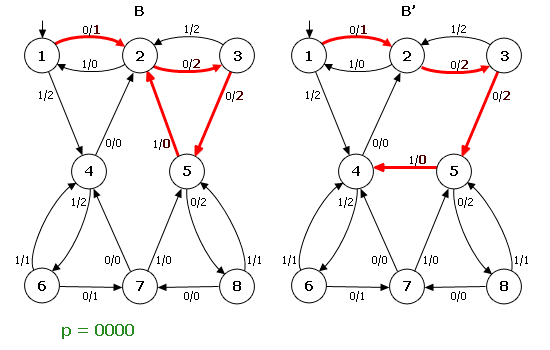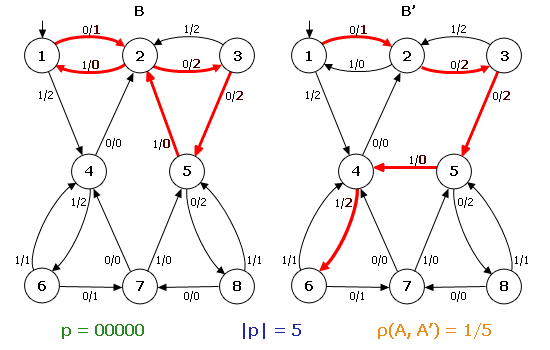
Рисунок 2 – Пример переброски одной дуги в автомате ОД–3
(анимация: 10 кадров, размер – 550х350, 146 килобайт)
(p – различающее слово, |p| – длина различающего слова, ρ(A, A′) – мера близости)
Непосредственно из теоремы 1 вытекает следующее утверждение, в котором описывается структура класса К(А).
Пусть А′ есть результат переброски дуги (t,x,y,u) в состояние v и d – длина кратчайшего входного слова w, для которого δ(s0,w)=t. Пусть также с – длина кратчайшего слова, различающего состояния u и v. Тогда справедлива следующая теорема.
Теорема 2. Класс Ki(A) состоит из всех тех автоматов А′, для которых выполняется следующее условие: d+с+1=i.
Полное доказательство теоремы 2 будет приведено в тексте магистерской работы.
Выводы
В работе получены следующие результаты:
- Найдена мера близости поведения эталона, являющегося инициальным ОД–k–автоматом, и автомата, полученного из эталона переброской одной дуги.
- Найдена верхняя оценка указанной меры близости и показано, что она достижима.
- Описана структура классов автоматов, обладающих заданной степенью близости по поведению относительно эталона.
Данное описание структуры классов может быть положено в основу алгоритма их построения.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2014 года. Полный текст работы и материалы по теме могут быть получены у автора или его научного руководителя после указанной даты.
Список источников
- Кудрявцев В.Б., Грунский И.С., Козловский В.А. Анализ поведения автоматов // Дискретная математика. – 2009. – 21, №1. – С. 3–35.
- Bhattacharyya A. Checking experiments on sequential machines. – New York: J. Wiley and Sons, 1989. – 155 с.
- Гилл А. Введение в теорию конечных автоматов. М.: Наука, 1966. – 272 с.
- Кудрявцев В.Б., Алешин С.В., Подколзин А.С. Введение в теорию автоматов. – М.:Наука, 1985. – 320 с.
- Грунский И.С., Козловский В.А., Пономаренко Г.Г., Представления конечных автоматов фрагментами поведения. – К.:Наукова думка, 1990. – 229 с.
- Козловский В.А. О структуре контрольных экспериментов с автоматом // Кибер нетика. – 1978. – № 3. – С. 19–33.
- Грунский И.С., Копытова О.М. О структуре контрольного эксперимента для определенно–диагностируемого автомата // Теория управляющих систем. – К.: Наук.думка, 1987. – С. 40–54.
- Копытова О.М. О структуре автоматов, сохраняющих поведение при перебросках дуг // Труды VIII Международной конференции "Дискретные модели в теории управляющих систем". – М.: Макс–Пресс, 2009, C. 155–159.
- Копытова О.М. Устойчивость автоматов к неисправностям их функции переходов // Труды ИПММ АН Украины. – 2010. – № 21. – С. 57–66.
- Бурлаева Е.И., Копытова О.М. Об одном типе локальных преобразований автомата // Материалы IV всеукраинской научно–технической конфиренции студентов, аспирантов и молодых ученых
Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2013)
(24.04–25.04.2013). Донецк: ДонНТУ, 2013. – C. 479–484. - Копытова О.М. О возможности сохранения поведения автомата при перебросках дуг // Материалы VI Международной научно–практической конференции
Новости научной мысли – 2010
(27.10–05.11.2010), Чехия. Прага. Издательский домОбразование и наука
, 2010 – C. 41–46. - Капитонова Ю.В., Кривий С.Л., Летичевский А.А., Луцкий Г.М., Печурин Н.К. Основы дискретной математики. – К.: Наукова думка, 2002. – 568 с.
- Кудявцев В.Б., Грунский И.С., Козловский В.А. Анализ и синтез абстрактных автоматов //Фундаментальная и прикладная математика. – Т. 15, № 4. – 2009. – С. 101–175.
