Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета та задачі дослідження
- 3. Автоматна модель
- 4. Задача аналізу поведінки скінченних автоматів
- 5. Формальна постановка задачі
- 6. Отримані теоретичні результати
- Висновки
- Перелік посилань
Вступ
Модель скінченного автомата широко використовується для опису різноманітних дискретних систем і процесів. Ці системи можуть піддаватися зовнішнім викривляючим впливам, і, як результат, змінювати свою поведінку. У багатьох випадках такі впливи носять локальний характер і можуть бути описані системою локальних перетворень над дугами початкового автомата–еталона. У зв'язку з цим виникає завдання порівняльного аналізу поведінки початкового і перетвореного автоматів і обчислення близькості цих автоматів по поведінці. У цій роботі досліджується вплив одного перекидання на поведінку ініціального визначено–діагностуємого порядку k еталона з точки зору визначення ступеня близькості його поведінки до і після перекидання.
1. Актуальність теми
Теоретичне і практичне значення моделей автоматів в дослідженні процесів формування та передачі сигналів у складних системах, вирішенні завдань технічного діагностування і проектування стало причиною інтенсивних досліджень теорії автоматів як математичної моделі складних систем. В даний час практично в будь–якій сфері людської діяльності зустрічається поняття система
. Скінченний автомат є однією з найбільш простих математичних моделей складних систем.
Автомати використовуються в криптографії та інших областях захисту інформації. Зокрема, вони природним чином дозволяють описувати потокові алгоритми шифрування. У зв'язку з цим дослідження моделі скінченного автомата є актуальним, а, отже, і вивчення поведінки автомата.
2. Мета та задачі дослідження
Об'єкт дослідження: аналіз поведінки скінченного приведеного ініціального автомата.
Предмет дослідження: знаходження довжини найкоротшого вхідного слова, що розрізняє початковий автомат–еталон і автомат, отриманий в результаті перекидань деяких дуг у графі переходів початкового автомата.
Метою випускної роботи магістра є розробка методу аналізу автоматів, породжуваних локальними перетвореннями еталона.
Основні задачі дослідження:
- Провести порівняльний аналіз поведінки ОД–k–еталона і автоматів, породжуваних його локальними перетвореннями.
- Пошук міри близькості поведінки еталона, що є ініціальним ОД–k–автоматом, і автомата, отриманого з еталона перекиданням однієї дуги.
- Для будь перекидання дуги оцінити міру близькості.
- Нехай К(А) – клас автоматів локально породжених з еталона А. Завдання полягає в тому, щоб описати структуру цього класу з точки зору розбиття його на підкласи автоматів, еквівалентних за ступенем близькості їх поведінки поведінці еталона.
3. Автоматна модель
Порівняння поведінки автоматів, одержаних у результаті перекидань дуг, почнемо з окремого випадку: як еталон будемо розглядати визначено–діагностуємий порядку k автомат, а під перекиданням будемо розуміти перекидання рівно однієї дуги.
Під моделлю автомата будемо розуміти ініціальний приведений визначено–діагностуємий порядку k (ОД–k) автомат Мілі A = (S, X, Y, δ, λ, s0), де S, X, Y – кінцеві множини станів, вхідних і вихідних символів відповідно, δ, λ – функції переходів і виходів, а s0 – початковий стан. При необхідності, щоб не виникало плутанини, до позначень цих об'єктів доданий індекс A чи значок штриха.
Автомат A називається ініціальним, якщо в множині його станів виділено якийсь стан s0, який називається початковим. При функціонуванні ініціального автомата вважається, що в початковий момент часу (перед подачею на його вхід деякого слова) автомат знаходиться в початковому стані s0.
У автоматі функції δ і λ звичайним чином поширюються на множину X* всіх вхідних слів кінцевої довжини. Нагадаємо, що автомат А називається ОД–k–автоматом, якщо k≥1 – найменше ціле таке, що для будь–якого вхідного слова p довжини k і будь–якої пари різних станів s∈S виконується нерівність λ(s, p) ≠ λ′(t, p), тобто з будь–якого породжуваного автоматом вхід–вихідного слова довжини k однозначно визначається початковий стан автомата.
Нехай вхід–вихідне слово w = (p, q) породжується станом s автомата А, якщо λ (s, р) = q. Довжину слова w позначимо |w|. Два стани s і t одного і того ж автомата A або двох різних автоматів A і B відповідно, називаються еквівалентними, якщо для всякого вхідного слова р′∈X* виконується λ(a,p)=λ′(b,p), де λ′ – функція виходів автомата A або B. Автомат називається приведеним, якщо всі його стани попарно нееквівалентні. Кожному стани s поставимо у відповідність множину λs всіх вхід–вихідних слів, породжуваних цим станом. Під поведінкою автомата А будемо розуміти множину λs0 вхід–вихідних слів, породжуваних його початковим станом.
Автомат зручно задавати у вигляді графа переходів, вершини якого відповідають станам з S, а дугами є четвірки (s, x, y, t), де t = δ (s, x), y = λ (s, x). Пара (x, y) називається відміткою дуги, s – її початком, а t – кінцем. Якщо e = (t, x, y, u) – дуга в графі переходів автомата A, то перекиданням цієї дуги зі стани u в стан v, відмінне від u, називаємо заміну її дугою (t, x, y, v).
4. Задача аналізу поведінки скінченних автоматів
Автомати, близькі за поведінкою в тому чи іншому сенсі, досліджуються досить давно, як і структура їх класів [1]. Головним чином це завдання розглядалася в рамках теорії експериментів з автоматами [2].
Муром було покладено основу теорії експериментів з автоматами. Його дослідження торкалися два взаємопов'язаних аспекти: невідмінність автоматів ніякими кратними і ніякими простими (однократними) експериментами; розпізнавання автоматів і їх станів за допомогою таких експериментів. Становлення теорії експериментів тісно пов'язане з роботами AM Богомолова та його учнів, М.П. Василевського, А. Гілла, В.Н. Носкова, Н.В. Євтушенко, А.Ф. Петренко, І.К. Рисцова, В. А. Твердохлебова, С.В. Яблонського, Ф. Хенні, П. Штарке та багатьох інших. Ці дослідження розділені на три етапи: комбінаторний, складностний і характерізаціонний.
Комбінаторний етап стосувався побудови засобів аналізу автоматів та алгоритмів проведення експериментів з ними, виходячи з комбінаторно–потужностних міркувань. Методи і результати цього етапу досить повно представлені у відомій книзі А. Гілла [3].
На складностному етапі основна увага приділяється побудові оптимальних за складністю алгоритмів і знаходженню складності проведення експериментів, а також оптимальних за складністю методів аналізу поведінки автомата. З’явилася необхідність аналізу структури експериментів. Цей етап ініційований роботами Ф. Хенні і М.П. Василевського, які проводили побудови контрольних експериментів шляхом розміщення у вхідні послідовності спеціальних підпослідовностей (діагностичних, настановних, локалізуючих, характеристичних і т. п.), з реакції на які досліджуваного автомата можна ідентифікувати його внутрішні стани. На цьому етапі досліджувалися різні види таких послідовностей і способи їх розміщення в експерименті. Методи і результати другого етапу досить повно представлені в книзі В.Б. Кудрявцева, С.В. Альошина, А.С. Подколзіна [4]. І.С. Грунський першим назвав ці послідовності і реакції на них ідентифікаторами станів, почав їх систематичне вивчення і звернув увагу на існування ідентифікаторів інших компонент поведінки, що не спостерігаються (наприклад, вхідних послідовностей [5]). На другому етапі отримано велику кількість приватних способів побудови контрольних та розпізнають експериментів для випадків, коли вони явно існують. Недослідженими залишилися умови існування та структура таких експериментів в загальному випадку. Дуже важким виявився питання: що повинно бути присутнім в цих експериментах, а що є витратами алгоритмів їх побудови, тобто питання характеризації вищевказаних експериментів. Поява перших характерізаціонних теорем [6] можна віднести вже до становлення третього, характерізаціонного, етапу.
Теорія експериментів інтенсивно розвивається, в ній отримано ряд важливих і принципових результатів пов'язаних з аналізом поведінки автоматів. Вплив перекидань дуг на поведінку автомата вивчалося в [7–11], досліджуючи дані роботи, стало відомо:
- Перекидання рівно про однієї дуги в приведеному автоматі завжди викликає зміну поведінки – автомат стає нееквівалентним початковому приведеному автомату.
- Перекидання однієї дуги завжди призводить до неізоморфного автомату.
- Перекидання двох дуг може привести до автомата, еквівалентного початковому.
- Для будь–якого натурального k>1 існує приведений автомат, в якому знайдеться підмножина з k дуг, одночасна перекидання яких призводить до ізоморфного автомата.
- При перекидах двох дуг вхідні–вихідні позначки на перекинутих дугах повинні збігатися.
- можливі перекидання більш двох дуг, при яких вхідні–вихідні позначки на перекинутих дугах різні;
- Доведені достатні умови ізоморфізму автоматів при перекидання двох дуг.
- Представлена структура автоматів, в яких можливе перекидання будь–якого числа дуг ≥ 2. Ці автомати не є сильно зв’язними.
- Перекидання дуг, що зберігає ізоморфізм, можливе в автоматах, що володіють певною симетрією графа переходів, яка відображається і в циклічній структурі графа.
- Існують приклади сильно зв'язкових автоматів, в яких існує ≥ 4–х перекидань, що зберігають ізоморфізм.
5. Формальна постановка задачі
Основні поняття теорії автоматів можна знайти в [12].
Нехай автомат A′ отримано з автомата A довільній перекиданням однієї дуги. Будемо для визначеності вважати, що в результаті перекидання відбулася заміна дуги (t, x, y, u) на дугу (t, x, y, v), де t,u,v′S, u≠v. Стани автомата A′ будемо позначати штрихом так, що перекинута дуга в ньому має вигляд e′ = (t′, x, y, v′). Отриманий автомат A′ назвемо автоматом, локально породженим з еталона А. Позначимо через K(A) клас всіх автоматів, локально породжених з автомата А, включаючи сам еталон. Інтерес представляють наступні питання: 1) як визначити ступінь близькості поведінки автоматів А і A′; 2) наскільки змінилася поведінка автомата після перекидання дуги; 3) яка структура класу K(A) з точки зору розбиття його на підкласи автоматів, еквівалентних за ступенем близькості їх поведінки поведінці еталона.
Формалізуємо поставлене завдання. Введемо на класі автоматів беровську метрику [7] таким чином. Нехай i – довжина деякого найкоротшого вхідного слова р, що розрізняє початкові стани s0 і s′0 автоматів А і A′ відповідно, тобто слова, для якого λ(s0, р) ≠ λ′(s′0, р). Тоді покладемо:
![]()
Ясно, що, чим довше розрізняє слово р, тим менше відстань між А і A′. Нехай |X| = m і |S| = n. Кожна дуга закінчується в одному з n станів, і, отже, її можна перекинути в один з решти (n-1) станів. Так як число дуг дорівнює mn, то кількість можливих перекидань дорівнює mn (n-1), і, значить, клас К(А) складається з (mn*(n-1)+1) автоматів, включаючи еталон. Даний клас розбивається на підкласи Ki(A) автоматів, що знаходяться на однаковій відстані від еталону. За визначенням, ρ(A, A′)=0, і тоді K0(A)={A}. Відомо [13], що перекидання однієї дуги завжди призводить до неізоморфного автомату. Тому початкові стани (s0, s′0) автоматів А і A′ завжди розрізнені деяким словом, і, значить, ρ(A, A′)>0. Зауважимо, що при перекиданні дуги її відмітка не змінюється, тобто стани s0 і s′0 видають одну і ту ж реакцію на кожен вхідний символ. Отже, довжина розрізненого їх слова більше або дорівнює 2, звідки ρ(A, A′)≤1/2 і К1(А)=∅. З іншого боку, пара станів (s0, s′0) завжди розрізнена деяким вхідним словом довжини, що не перевершує (2n -1), тому ρ(A, A′)≥(2n-1). Таким чином, 1/(2n-1)≤ρ(A, A′)≤1/2. Отже, для класу К (А) існує розбиття на підкласи:
![]()
6. Отримані теоретичні результати
Теорема 1. Нехай А – ініціальний приведений ОД–k–автомат і отриманий з А перекиданням дуги (t, x, y, u) у стан v. Тоді ρ(A, A′)≤1/(d+k+1), де d – довжина найкоротшого вхідного слова w такого, що δ (s0, w) = t.
Доказ. Щоб відрізняти стани автомата A від станів, будемо стани останнього позначати штрихом і пару (s, s′) називати подвійними, де s=S, s′=S′. Покажемо спочатку, що стани u і v′ розрізнені деяким словом довжини, не більше k. Для цього скористаємося прийомом, використаним при доказі того факту, що перекидання дуги в будь–якому приведеному автоматі завжди призводить до автомата, що не ізоморфний початковому [7]. Побудуємо автомат В, рівний прямий сумі автоматів А і А′, і розглянемо процес побудови Рk–таблиць [3] для автомата B.
Оскільки таблиці виходів автоматів А і А′ збігаються, то в таблиці Р1 кожен клас еквівалентності складається з пар подвійних станів. Зауважимо, що будь–яка пара (s, s′), крім пари (t, t′), по будь–якому х знову переходить в пару подвійних станів. Пара (t, t′) – єдина, для якої це не виконується, так як δB(t,x)=u і δB(t′,x)=v′. Звідси випливає, що поки стани (t, t′) k–еквівалентні, будь–яка пара (s, s′), відмінна від (t, t′), буде (k+1)–еквівалентної. Сама ж пара (t, t′) k–еквівалентна, поки пара (u, v′) є (k-1)–еквівалентної. Але, якщо (u, v′) (k-1)–еквівалентна, то тоді пари (t, t′), (u, u′), (v, v′) k–еквівалентні і, значить, стани u, u′, v, v′ належать одному класу еквівалентності в таблиці Рk. Так як А ОД–k–автомат, то для деякого i<k стани u і v будуть (i-1)–еквівалентні, але i–розрізнені. Тоді i–розрізненими будуть і стани u і v′, де i ≤ k.
Нехай тепер w – найкоротше вхідне слово в автоматі А, що переводить його з початкового стани в стан t, і р – найкоротша слово, що розрізняє u і v′. Нехай |w| = d, |p| = i, і як показано вище, i ≤ k. Ясно, що в автоматі А′ δ(s′0, w)=t′. Тоді δ(s0, wx)=u, δ(s′0, wx)=v′, λ(s0, wx)=λ(s′0, wx), але λ(s0, wxp)≠λ(s′0, wxp), причому |wxp| ≤ d+1+k, що і потрібно було довести.
Покажемо, що отримана оцінка відстані досяжна.
На малюнку 1 приведений ініціальний автономний автомат А. Нехай автомат А′ є результатом перекидання однієї дуги в автоматі А: дуга (6,0,2,5) перекидається в стан 3 і замінюється дугою (6′, 0, 2, 3′). Оскільки перекидається дуга, яка виходить із стани 6, то найкоротший слово w має довжину d = 3. Легко бачити, що λ (s0, 0000) = λ (s′0, 0000), але λ(s0, 00000)≠λ(s′0, 00000). Тому p = 00000 і |p| = 5. Звідси ρ(A, A′)=1/5. На прикладі видно, що в результаті перекидання дуги автомата А′ став неприведеним автоматом, бо стани 5 і 6 стали еквівалентними.
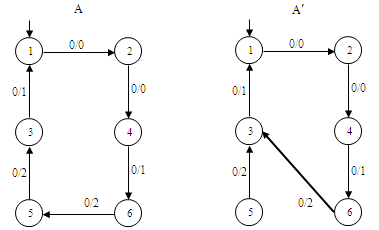
Рисунок 1 – Приклад перекидання однієї дуги в автоматі ОД–2
Тепер розглянемо ОД–3–автомат B (рис. 2). Нехай автомат B′ є результатом перекидання однієї дуги в автоматі B: дуга (5,1,0,2) перекидається в стан 4 і замінюється дугою (5′, 1, 0, 4′). Оскільки перекидається дуга, яка виходить із стани 5, то найкоротше слово w має довжину d = 3. Легко бачити, що λ (s0, 0001) = λ (s′0, 0001), але λ(s0, 00011)≠λ(s′0, 00011). Тому p = 00011 і |p| = 5. Звідси ρ(B, B′)=1/5. На прикладі видно, що в результаті перекидання дуги автомат B′ залишився ОД–3.
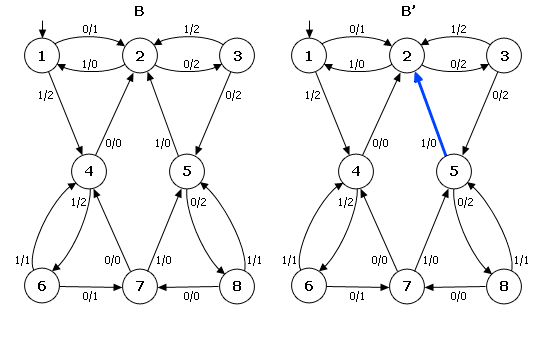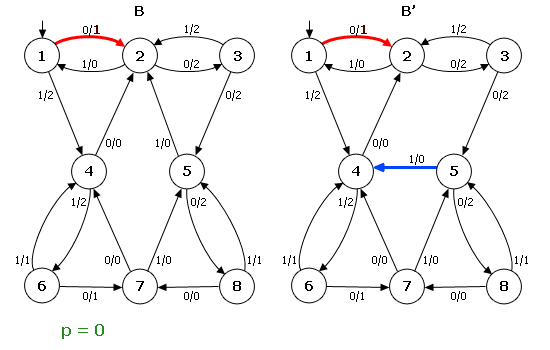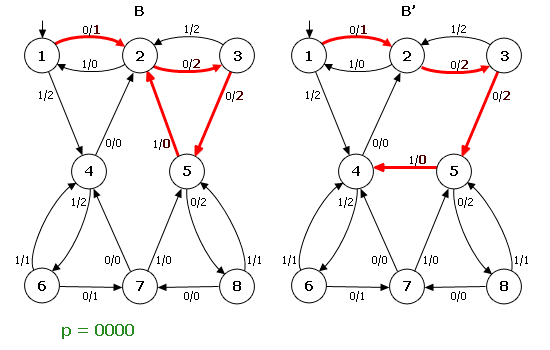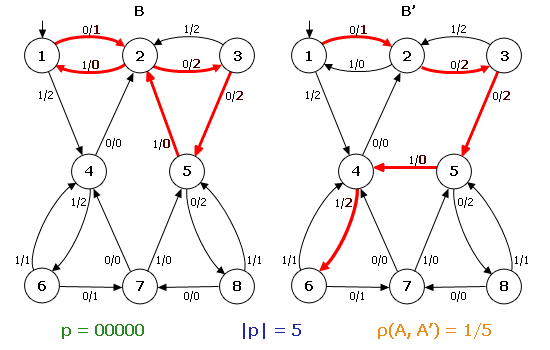
Рисунок 2 – Приклад перекидання однієї дуги в автоматі ОД3
(анімація: 10 кадрів, розмір – 550х350, 146 кілобайт)
(p – розрізняюче слово, |p| – довжина розрізняючого слова, ρ(A, A′) – міра близкості)
Безпосередньо з теореми 1 випливає наступне твердження, в якому описується структура класу К(А).
Нехай А′ є результат перекидання дуги (t, x, y, u) у стан v і d – довжина найкоротшого вхідного слова w, для якого δ (s0, w) = t. Нехай також c – довжина найкоротшого слова, що розрізняє стани u і v. Тоді справедлива наступна теорема.
Теорема 2. Клас складається з усіх тих автоматів А′, для яких виконується така умова: d + с + 1 = i.
Повний доказ теореми 2 буде приведений у тексті магістерської роботи.
Висновки
У роботі отримані наступні результати:
- Знайдена міра близькості поведінки еталона, що є ініціальним ОД–k–автоматом, і автомата, отриманого з еталона перекиданням однієї дуги.
- Знайдена верхня оцінка зазначеної міри близькості і показано, що вона досяжна.
- Описана структура класів автоматів, що володіють заданим ступенем близькості з поведінки щодо еталона.
Даний опис структури класів може бути покладений в основу алгоритму їх побудови.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2014 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його наукового керівника після вказаної дати.
Перелік посилань
- Кудрявцев В.Б., Грунский И.С., Козловский В.А. Анализ поведения автоматов // Дискретная математика. – 2009. – 21, №1. – С. 3–35.
- Bhattacharyya A. Checking experiments on sequential machines. – New York: J. Wiley and Sons, 1989. – 155 с.
- Гилл А. Введение в теорию конечных автоматов. М.: Наука, 1966. – 272 с.
- Кудрявцев В.Б., Алешин С.В., Подколзин А.С. Введение в теорию автоматов. – М.:Наука, 1985. – 320 с.
- Грунский И.С., Козловский В.А., Пономаренко Г.Г., Представления конечных автоматов фрагментами поведения. – К.:Наукова думка, 1990. – 229 с.
- Козловский В.А. О структуре контрольных экспериментов с автоматом // Кибер нетика. – 1978. – № 3. – С. 19–33.
- Грунский И.С., Копытова О.М. О структуре контрольного эксперимента для определенно–диагностируемого автомата // Теория управляющих систем. – К.: Наук.думка, 1987. – С. 40–54.
- Копытова О.М. О структуре автоматов, сохраняющих поведение при перебросках дуг // Труды VIII Международной конференции "Дискретные модели в теории управляющих систем". – М.: Макс–Пресс, 2009, C. 155–159.
- Копытова О.М. Устойчивость автоматов к неисправностям их функции переходов // Труды ИПММ АН Украины. – 2010. – № 21. – С. 57–66.
- Бурлаева Е.И., Копытова О.М. Об одном типе локальных преобразований автомата // Материалы IV всеукраинской научно–технической конфиренции студентов, аспирантов и молодых ученых
Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2013)
(24.04–25.04.2013). Донецк: ДонНТУ, 2013. – C. 479–484. - Копытова О.М. О возможности сохранения поведения автомата при перебросках дуг // Материалы VI Международной научно–практической конференции
Новости научной мысли – 2010
(27.10–05.11.2010), Чехия. Прага. Издательский домОбразование и наука
, 2010 – C. 41–46. - Капитонова Ю.В., Кривий С.Л., Летичевский А.А., Луцкий Г.М., Печурин Н.К. Основы дискретной математики. – К.: Наукова думка, 2002. – 568 с.
- Кудявцев В.Б., Грунский И.С., Козловский В.А. Анализ и синтез абстрактных автоматов //Фундаментальная и прикладная математика. – Т. 15, № 4. – 2009. – С. 101–175.
