Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і завдання дослідження, плановані результати
- 3. Огляд досліджень та розробок
- Висновки
- Список джерел
Вступ
Питанням зрівнювання геодезичних мереж приділяється велика увага. Вони використовуються при вирішенні задачі оцінювання деформацій, при зрівнянні фотограмметричних задач, в задачах оптимізації мереж. Як приклад ефективного застосування висотних мереж можна привести завдання аналізу стійкості реперів висотної основи.
Слід також зазначити, що з позиції системного підходу мережі являють собою більш цілісне побудова, тоді як мережі невільні є їх окремими випадками. Тому іноді доцільно геодезичні мережі зрівнювати як вільні, а потім перетворювати на невільні, фіксуючи будь вихідні дані.
Існує багато методів для отримання оцінок невідомих параметрів при зрівнюванні геодезичних мереж, наприклад: метод найменших квадратів, метод Коші, метод найменших модулів, метод найменших модулів, метод минимакса, метод найменших позитивних квадратних форм і т.д.
1. Актуальність теми
Як відомо, створення інженерно-геодезичних мереж відрізняється рядом особливостей, зумовлених тим, що їх проектування виконується для конкретного об'єкта (часто на забудованій території). На відміну від загально геодезичних мереж інженерно-геодезичні мережі мають складну конфігурацію, характеризуються порушенням геометричних вимог, що пред'являються до геодезичних мереж. Крім того точність в інженерно-геодезичних мережах, які передбачають винесення в натуру окремих елементів конструкцій, підвищується в міру деталізації об'єкту, що будується. Тому всі мержі мають похибку в вимірах та їх потрібно зрівнювать.
2. Мета і завдання дослідження, плановані результати
Мета і завдання дослідження: порівняти оцінки невідомих параметрів, яку можна отримати при зрівнюванні геодезичних мереж методом Коші і методом найменших квадратів.
Для виявлення найбільш ефективного порівняння та аналізу зрівнювання методом Коші і методом найменших квадратів виконуються наступні практичні завдання:
- Зрівняння равноточних вимірювань, порівняння та аналіз результатів;
- Зрівняння неравноточних вимірювань, порівняння та аналіз результатів;
- Зрівняння геодезичної мережі, порівняння та аналіз результатів.
Об'єкт дослідження: Інженерно-геодезичні мережі.
Предмет дослідження: зрівнювання інженерно-геодезичних мереж раніше мало дослідженим методом Коші і порівняння результатів з методом найменших квадратів.
В рамках магістерської роботи планується отримання актуальних наукових результатів за наступними напрямками:
- Аналіз способів зрівнювання інженерно-геодезичних мереж.
- Визначення оптимального способу зрівнювання інженерно-геодезичних мереж.
- Вплив похибок на результати зрівнювання.
3. Огляд досліджень та розробок
В даний час приділяється все більшу увагу питанням вирівнювання геодезичних мереж. В першу чергу пояснимо, що ми будемо розуміти під геодезичної мережею в контексті даної роботи.
Геодезична мережа – це система закріплених на поверхні землі точок (геодезичних пунктів) і взаємно визначених на карті / щодо існуючих об'єктів у плані та по висоті.
Існують різні методи побудови мереж.
При побудові планових мереж окремі пункти мережі служать вихідними – їх координати повинні бути відомі. Координати інших пунктів визначають за допомогою вимірювань, що пов'язують їх з вихідними. Планові геодезичні мережі створюють наступними методами.
Триангуляція – метод визначення планового положення геодезичних пунктів шляхом побудови на місцевості мережі трикутників, в яких вимірюють кути, а також довжини деяких сторін, званих засадничими сторонами (рис. 1).
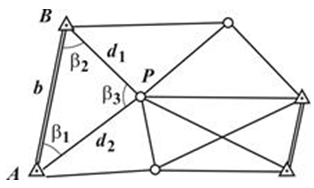
Рисунок 1.– Схема мережі тріангуляції
Продовжуючи подібним чином, обчислюють довжини всіх сторін мережі. Якщо, крім базису b відомі інші базиси (на рис. 1 базиси показані подвійною лінією), то довжини сторін мережі можна обчислити з контролем.
Координати пункту P визначаться за формулами кутової засічки. Аналогічно обчислюють координати всіх інших пунктів.
Трилатерація – метод визначення планового положення геодезичних пунктів шляхом побудови на місцевості мережі трикутників, у яких вимірюють довжини їх сторін.
Якщо в трикутнику АВP (рис. 1) відомий базис і виміряні сторони, то на основі лінійної засічки, можна обчислити кути треугольніка.Так ж обчислюють кути всіх трикутників, а потім, як і в тріангуляції, – координати всіх пунктів.
Полігонометрія – метод визначення планового положення геодезичних пунктів шляхом прокладання ламаної лінії (полігонометрічеського ходу) або системи пов'язаних між собою ламаних ліній (мережі полігонометрії), в яких вимірюють кути повороту і довжини сторін.
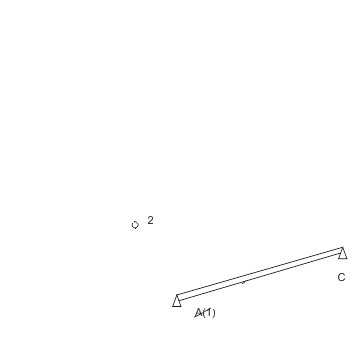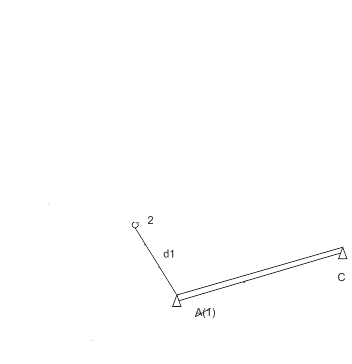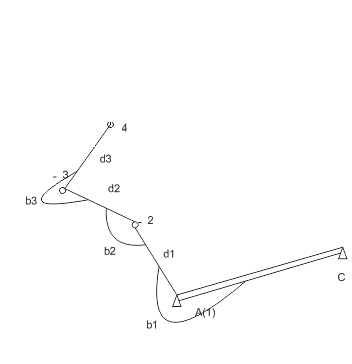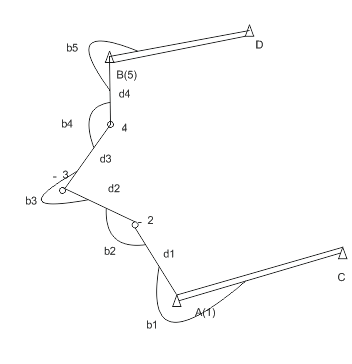
Рисунок 2.– Побудова мережі полігонометрії
(анімація: 5 кадрів, 10 циклів повторення, 20 кілобайт)
Схема полігонометричного ходу показана на рис. 2 a, де A і B – вихідні пункти; CA і BD – вихідні напрямки, кути дирекцій яких відомі; 1, 2, 3, 4, 5 точки (вершини) ходу; b – виміряні горизонтальні кути; d – виміряні довжини сторін (i = 1, 2, ...).
Супутниковий метод визначення координат геодезичних пунктів заснований на вимірах за сигналами супутників навігаційних систем ГЛОНАСС (Росія) і GPS (США), виконуваних двома (і більше) наземними приймачами. За результатами вимірювань з високою точністю визначають різниці dx, dy, dz геоцентричних координат між пунктами. Якщо координати одного з пунктів відомі, то, додавши до них виміряні різниці, знаходять координати інших пунктів. Потім координати перетворять в геодезичні або плоскі прямокутні [9].
Яким би методом не знаходились координати пунктів то вони несуть у собі помилки. Для виключення помилок і зрівнюють геодезичні мережі. Для вирівнювання геодезичних мереж складають з невідомими оцінками до координат матриці з коефіцієнтами ваг біля невідомих і вільними членами.
Розглянемо два методи зрівнювання геодезичних вимірювань: метод Коші і метод найменших квадратів.
Метод обробки геодезичних вимірювань Коші.
Розглянемо схему зрівнювання за елементами. Для простоти і без порушення спільності покладемо Х0 = 0, так що система фундаментальних рівнянь прийме вигляд.
Y = L – D = XA,
де Y – матриця вільних членів,
Х – матриця коефіцієнтів при невідомих,
А – вектор стовпець невідомих.
Або, докладніше,
yr = lr – dr = [Хrj aj] (r = 1, 2,….N) (1.1)
Спостереження передбачаються равноточнимі. Ми бачили, що при нормальності вектора похибок d метод найменших квадратів має деякі екстремальні властивості серед широкого класу інших методів, так що його застосування в цьому сенсі вигідно. Але в обчислювальному відношенні рішення системи нормальних рівнянь, незважаючи на зазвичай вживані спрощують прийоми, все ще становить труднощі. Тому іноді вдаються і до інших методів оцінюючи аj за спостереженнями lr (r = 1, 2 ..., N) і фундаментальним рівнянням.
Складання нормальних рівнянь і отримання з їх допомогою оцінок для параметрів (а1, ...., А n) є, в кінцевому рахунку, метод такого комбінування N рівнянь з похибками надлишкової системи, щоб в результаті можна було отримати розв'язні систему лінійних рівнянь щодо n параметрів ( а1, ...., а n). Таких методів може бути багато, крім методу найменших квадратів. Хоча, як пояснено вище, вони не будуть уже мати екстремальних властивостей, притаманних методу найменших квадратів. Один з таких методів був запропонований О. Коші.
Тут ми викладемо коротко його зміст.
Прямий хід. Припис О. Коші полягає в наступному. Спочатку система (1) готується, тобто множенням кожного рівняння на +1 або –1 домагаються того, що х1j>0 (j = 1,2 ... ..N). Припустимо, що це вже зроблено. Далі, всі рівняння складаються, так що виходить:
(х11 + х21…+ хN1)a1+(x12+x22+… + xN2)a2+….+(x1n+ x2n+…+ xNn)an=y1+…+yN.
Будемо дотримуватися позначень Коші, вважаючи
x1j+x2j+…+ xNj=Sxj ( j = 1,2, …, n)
Маємо тоді
a1Sx1+…+ anSxn =Sy
В силу попереднього, Sx1>0. Деля на Sx1, отримуємо:
а1 + а2 * S_(x_2 )/S_(x_2 ) +аn *S_(x_n )/(Sx_1 ) = Sy/(Sx_1 ) (1.2)
Множимо (1.2) відповідно на х11, х12 .... x1N і віднімаємо з отриманих N рівнянь рівняння системи (1.1); тоді члени, що містять а1, зникають і виходить система з N рівнянь з (n – 1) невідомими А2, ...., аn
(x12 – x11 (Sx_2)/(Sx_1 ) ) a2+… +( xnn – x11 (Sx_n)/(Sx_1 ) ) an = y1 – x11 Sy/(Sx_1 ) ,
(xN2 – xN1 (Sx_2)/(Sx_1 ) ) a2+…. +(xNn – xN1 (Sx_n)/(Sx_1 ) ) an = yN – xN1 Sy/(Sx_1 )
Далі, готуємо так само нову систему і виробляємо з нею такі ж операції. Зрештою, взагалі кажучи, отримуємо систему N рівнянь з одним невідомим аn
x'rnan = y'r ( r = 1, 2,…., N );
де хrn '> 0 – отримані коефіцієнти, а y'r – лінійні комбінації з yq (q = 1, 2, ... .N), отримані в процесі роботи.
Далі, замінюємо в кожному з y'r невідомі нам yq на відомі і спостерігаємо yq. Результат такої заміни позначимо l'r. Після цього знаходимо а'n з рівнянь
a'n = (Sl_r)/(Sx_(r ) )
Зворотний хід. Підставляємо останнім невідоме в матрицю (1.1), залишаємо невідомі в лівій частині рівняння, а відомі елементи переносимо в праву частину і застосовуємо ті ж формули, що і в прямому ході, до тих пір поки не знайдемо всі невідомі елементи. Формуємо вектор стовпець із знайдених невідомих [2].
Метод обробки геодезичних вимірювань метод найменших квадратів
Існує два підходи до вирішення завдання зрівнювання. Розглянемо їх по суті.
1. Візьмемо трикутник, де виміряні всі три кути (рис.3). Отже, має місце рівняння
b1+v1+b2+v2+b3+v3–180=0
де b – виміряні кути, v – поправки.
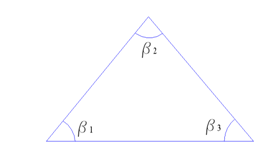
Рисунок 3.– Трикутник, де виміряні всі три кути
Позначивши:
b1+b2+b3–180=W
де W – нев'язка в трикутнику, можемо записати
v1+v2+v3+W=0. (2.1)
В (2.1) v1,v2,v3 – невідомі, а W – вільний член.
Ми отримали одне рівняння з трьома невідомими, яке має безліч рішень, тобто система є невизначеною.
2. Візьмемо систему трьох нівелірних ходів з однією вузловою точкою (рис.4.). Невідомою при цьому буде висота вузлової точки H.
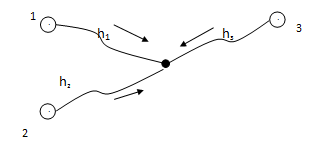
Рисунок 4 – Система трьох нівелірних ходів з однією вузловою точкою
Отже, можна записати три рівняння
H–H1–h1 = v1
H–H2–h2 = v2 (2.2)
H–H3–h3 = v3
де Hi – висоти вихідних реперів, H – висота вузлової точки, hi – виміряні перевищення.
Таким чином, ми маємо три рівняння з одним невідомим Н. Отже, ми знову отримали невизначену систему.
Принцип найменших квадратів та його обгрунтування.
Сутність рішення за принципом найменших квадратів полягає в тому, що системи вирішуються під умовою
[pvv] = min (2.3)
де р – ваги вимірювань, тобто під умовою мінімуму суми квадратів поправок, помножених на ваги вимірів. У разі равноточних вимірювань (2.3) приймає вигляд:
[vv] = min
Розглянемо рішення задачі зрівнювання за цим способом на прикладі системи (2.2).
Уявімо (2.2) у вигляді:
H–l1 = v1
H–l2 = v2
H–l3 = v3
де li = Hi + hi (i = 1,2,3), і підставимо в (2.3).
f (H) = p1v1v1 + p2v2v2 + p3v3v3 = p1 (H–h1) ^ 2 + p2 (H–h2) ^ 2 + p3 (H–h3) ^ 2
Щоб знайти мінімум функції f (H) візьмемо похідну по змінним hi і прирівняємо її нулю.
f '(H) = 2p1 (H–h1) + 2p2 (H–h2) + 2p3 (H–h3) = 0
або
2H (p1 + p2 + p3) –2 (h1p1 + h2p2 + h3p3) = 0
У результаті отримаємо:
H = [ph] / [p] (2.4)
Вираз (2.4) являє собою загальну арифметичну середину [ 5 ].
Щоб переконатися, що рішення (2.4) дійсно дає мінімум (2.3), знайдемо другу похідну:
f '(H) = 2p1 + 2p2 + 2p3 = 2 [p]> 0
Друга похідна позитивна. Отже,
f (H) = [pvv] = min
Підіб'ємо підсумок:
1. Ми отримали єдине рішення системи (2.2). При цьому воно виявилося загальної арифметичної серединою, що підтверджує єдність принципу найменших квадратів і принципу арифметичної середини.
2. З (2.3) і (2.4) випливає, що рішення (2.4) відповідає мінімуму функції (2.3) і відповідно мінімуму емпіричної середньоквадратичної похибки одиниці ваги:
mm = [pvv] / (n–1)
Отже, вага визначається величини, що дорівнює:
PH = c [p] / mm
де с – довільна позитивна постійна.
За будь–яких значеннях с, [p] PH буде максимальним [ 6 ].
Тому рішення, знайдене способом найменших квадратів відповідає найбільшому вазі визначається величини.
Стосовно до двох підходів, сформульованих нами в 2.2 у вигляді рівнянь (2.2) і (2.1) існує два способи зрівнювання:
1. Параметричний спосіб
2. Спосіб зрівнювання виміряних величин, пов'язаних умовами [ 3 ].
Параметричний спосіб зрівнювання.
Нехай для визначення значень невідомих x, y, z, ... t виконані равноточние незалежні вимірювання L1, L2, .., Ln. Загальне число невідомих t, загальне число вимірювань n. При чому n> t, тобто система невизначена.
Невідомими можуть бути координати пунктів, висоти реперів та інші величини, значення яких необхідно визначити.
Вимірюваними величинами в цьому випадку будуть горизонтальні напрямки, горизонтальні або вертикальні кути, довжини ліній, перевищення і т.д.
Між невідомими x, y, z ... t і виміряними величинами Li існують точні математичні залежності, які в загальному вигляді можна представити:
fi (x, y, x, .., t) = Li + Vi (2.5)
де Vi – поправки до виміряних значень Li.
На підставі (2.5) зможемо записати систему рівнянь поправок в загальному вигляді:
f1 (x, y, x, .., t) –L1 = V1
f2 (x, y, x, .., t) –L2 = V2 (2.6)
....................
fn (x, y, x, .., t) –Ln = Vn
Перед вирівнюванням рівняння (2.6) необхідно привести до лінійного вигляду. Для цього введемо наближені значення невідомих x0, y0, z0, .., t0 і поправки до цих наближеним значенням dx, dy, dz, .., dt тобто
x = x0 + dx
y = y0 + dy
z = z0 + dz (2.7)
.......
t = t0 + dt
Підставами (2.7) в (2.6)
fi (x0 + dx, yo + dy, z0 + dz, .., to + dt) –Li = Vi (2.6a)
Розкладемо функцію fi в ряд Тейлора, обмежуючись тільки першими ступенями поправок. В результаті отримаємо:
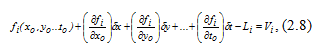
Рисунок 5.–Розкладання в ряд Тейлора функції fi
де i = (1,2, .., n)
Введемо позначення:

Рисунок 6.–Позначення
З урахуванням (2.7), (2.8), і (2.9) система рівнянь поправок (2.6) приймає вигляд:
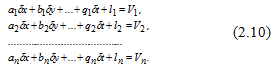
Рисунок 7.–Система рівнянь поправок
Загальне число рівнянь поправок дорівнює числу вимірювань n [ 8 ].
Візьмемо систему рівнянь поправок в лінійному вигляді. Щоб викладки були не такими громіздкими, обмежимося тільки трьома невідомими, маючи на увазі, що отримані результати можна буде поширити на будь–яке число невідомих. Отже,
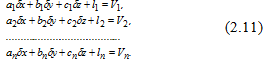
Рисунок 8.–Система рівнянь поправок с трьома невідомими
Кількість рівнянь більше числа невідомих. Число рівнянь n, число невідомих 3. Число надлишкових вимірювань r = n – 3, а тому система (2.11) не має єдиного рішення.
Знайдемо для цієї системи мінімум [vv]. Зведемо в квадрат ліві і праві частини рівнянь поправок (2.11), а результати складемо.
![Знаходження [vv] Знаходження [vv]](images/9.png)
Рисунок 9.–Знаходження [vv]
Щоб знайти мінімум [vv], візьмемо від функції (2.12) приватні похідні з невідомих dx, dz, dz і прирівняємо їх нулю
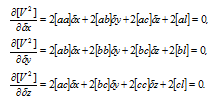
Рисунок 10.–Приватні похідні з невідомих
Скоротивши спільний множник 2, отримаємо
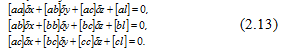
Рисунок 11.–Приватні похідні з невідомих скорочені на 2
У системі (2.13) число невідомих дорівнює числу рівнянь. Така система має єдине рішення. Ось чому рівняння (2.13) прийнято називати нормальними рівняннями.
У цій системі коефіцієнти при невідомих, розташовані по головній діагоналі, називають квадратичними, які завжди позитивні [ 4 ]. Коефіцієнти при невідомих, розташовані симетрично щодо головної діагоналі, попарно рівні між собою, тобто система (2.13) симетрична. Вирішивши цю систему, знаходимо невідомі dx, dy, dz. Підставляємо невідомі в (2.11) і знаходимо поправки.
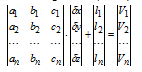
Рисунок 12.–Матричний вигляд системи рівнянь поправок
або скорочено:
ad + l = V (2.14)
Матриця a має розмір nxt, d–tx1, V–nx1.
Транспоніруем матрицю a і множимо її зліва почленно на вираз (2.14).
a ^ Tad + a ^ Tl = a ^ TV (2.15)
Розглянемо твори матриць, що входять в (2.15).
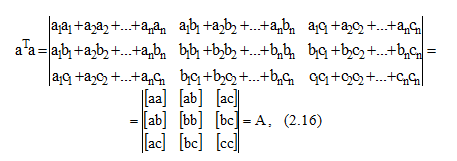
Рисунок 13.–Множення матриць a^T*a
т.е. ми отримали матрицю коефіцієнтів нормальних рівнянь (2.13) [ 10 ].
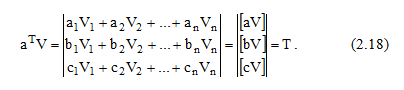
Рисунок 14.–Множення матриць a^T*V
Беручи до уваги (2.16) і (2.17), приходимо до висновку, що ліва частина виразу (2.11) є не що інше, як система нормальних рівнянь (2.9) в матричної формі. В (2.13) і (2.15) ліві частини рівні [ 1 ]. Отже, повинні бути рівні праві. Тому можемо записати
[aV] = 0; [bV] = 0; [cV] = 0 (2.19)
Система нормальних рівнянь набуває вигляду:
Ad + alfa = 0 (2.20)
Так як рівняння поправок (2.16) незалежні один від одного, матриця A неособлива. Отже, для вирішення рівняння (2.20) необхідно і достатньо помножити його зліва на матрицю A ^ –1, зворотну матриці A. В результаті матимемо:
d = –A ^ –1 * alfa (2.21)
Підіб'ємо підсумок. Зрівняння параметрическим способом здійснюється в такій послідовності:
1. Підраховуємо кількість обумовлених невідомих t, підраховуємо число незалежних вимірювань n і визначаємо число надлишкових вимірювань r = nt. Якщо n = t, r = 0, то завдання зрівнювання виміряних величин не виникає.
2. Використовуючи тільки необхідні вимірювання, визначаємо тим чи іншим способом наближені значення невідомих x0, y0, z0, .., t0.
3. Складаємо рівняння поправок в загальному вигляді (2.7), приводимо їх до лінійного вигляду (2.11). В результаті отримуємо коефіцієнти рівнянь поправок a, b, c, .., q.
4. Обчислюємо вільні члени рівнянь поправок за формулою (2.10).
5. Складаємо матрицю коефіцієнтів рівнянь поправок і матріцу– стовпець вільних членів l. Розмір матриці a (nxt), а матриці l (nx1). Складаємо рівняння поправок в матричної формі (2.16).
6. Транспоніруем матрицю a.
7. Множимо матричне рівняння (2.16) зліва на матрицю a ^ T. В результаті отримуємо систему нормальних рівнянь (2.15), представлену в матричної формі (2.21).
8. Знаходимо матрицю A ^ –1, зворотну матриці коефіцієнтів нормальних рівнянь A. Розмір тієї та іншої матриці txt.
9. Множимо рівняння (2.21) зліва на матрицю A ^ –1. В результаті отримуємо вектор-стовпець поправок d. Розмір матриці tx1.
10. Обчислюємо за формулою (2.8) зрівнялися значення невідомих x, y, ..., t.
11. Підставляємо вектор-стовпець d в рівняння (2.15), множимо і складаємо матриці. В результаті отримуємо матрицю-стовпець поправок до виміряних величин V. Розмір матриці nx1. Обчислюємо зрівнялися значення Li + Vi.
12. Оцінюємо точність отриманих в результаті зрівнювання невідомих величин x, y, .., t [ 7 ].
Висновки
При виконанні аналізу методів була проаналізована нормативна література і різні інтернет джерела описують найбільш раціональне застосування того чи іншого методу зрівнювання.
На момент написання реферату було написана мною програма в MathCAD з реалізації зрівнювання геодезичних мереж методом Коші, виповнилося зрівняння равноточних і неравноточних вимірювань і зроблено аналіз в порівнянні результатів розрахованих за методом Коші і методом найменших квадратів.
На підставі отриманих даних можемо зробити висновок, що використання методу найменших квадратів є кращий для виконання зрівнювання геодезичних мереж, т. К. Обчислюється оцінка з більшою точністю.
Планується проведення подальших досліджень.
На момент написання реферату, Магістерська робота ще не завершена. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після грудня 2015 року.
Список джерел
- Метод наименьших квадратов – [Электронный ресурс] –http://geodesy-book.narod.ru/Numerical_methods/05.pdf
- Метод наименьших квадратов и основы теории обработки наблюдений/ Ю. В. Линник. –М.:Государственное издательство физико-математической литературы, 1958 – с. 338.
- Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений: Учебное пособие для вузов.– М.:Недра, 1984, 352 с.
- Теория матриц./Ланкастер П. – М.: Наука, 1982. – 272 с.
- Чернова Н.И. Теория вероятностей: Учеб. пособие/ Сиб-ГУТИ. Новосибирск, 2007. – 128с.
- Губанов В.С. Обобщенный метод наименьших квадратов. Теория и применение в астрометрии. – М.: Наука, 1997. – 319с.
- Чеботарев А.С. Способ наименьших квадратов. – М.: Геодезический факультет и военно-геодезическое отделение Московского межевого института, Издательство Московского высшего технического училища, 1928. – 475 с.
- Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.: Физматгиз, 1963, 734 с.
- Методы и приборы высокоточных геодезических измерений в строительстве./ Под редакцией В.Д. Большакова. – М.: Недра, 1976.– 335 с.
- Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: – Наука. Главная редакция физико-математической литературы. 1984. – 320 с.
