Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- Выводы
- Список источников
Введение
Вопросам уравнивания геодезических сетей уделяется большое внимание. Они используются при решении задачи оценивания деформаций, при уравнивании фотограмметрических задач. Как пример эффективного применения высотных сетей можно привести задачу анализа устойчивости реперов высотной основы.
Следует также отметить, что с позиции системного подхода свободные сети представляют собой более целостное построение, тогда как сети несвободные являются их частными случаями. Поэтому иногда целесообразно геодезические сети уравнивать как свободные, а затем превращать в несвободные, фиксируя любые исходные данные.
Существует много методов для получения оценок неизвестных параметров при уравнивании геодезических сетей, например: метод наименьших квадратов, метод Коши, метод наименьших модулей, метод наименьших модулей, метод минимакса, метод наименьших положительных квадратных форм и т.д.
1. Актуальность темы
Как известно, создание инженерно-геодезических сетей отличается рядом особенностей, обусловленных тем, что их проектирование выполняется для конкретного объекта (часто на застроенной территории). В отличии от общих геодезических сетей инженерно-геодезические сети имеют сложную конфигурацию, характеризуются нарушением геометрических требований, предъявляемых к геодезическим сетям. Кроме того точность в инженерно-геодезических сетях, предусматривающих вынос в натуру отдельных элементов конструкций, повышается по мере детализации строящегося объекта. Поэтому все сети содержат погрешности измерения и их необходимо уравнивать.
2. Цель и задачи исследования, планируемые результаты
Цель и задачи исследования: сравнить оценки неизвестных параметров, которую можно получить при уравнивании геодезических сетей методом Коши и методом наименьших квадратов.
Для выявления наиболее эффективного сравнения и анализа уравнивания методом Коши и методом наименьших квадратов выполняются следующие практические задачи:
- Уравнивание равноточных измерений, сравнение и анализ результатов;
- Уравнивание неравноточных измерений, сравнение и анализ результатов;
- Уравнивание геодезической сети, сравнение и анализ результатов.
Объект исследования: инженерно-геодезические сети.
Предмет исследования: Уравнивания инженерно-геодезических сетей ранее мало исследованным методом Коши и сравнение результатов с методом наименьших квадратов.
В рамках магистерской работы планируется получение актуальных научных результатов по следующим направлениям:
- Анализ способов уравнивания инженерно-геодезических сетей.
- Определение оптимального способа уравнивания инженерно-геодезических сетей.
- Влияние погрешностей на результат уравнивания.
3. Обзор исследований и разработок
В настоящее время уделяется все большее внимание вопросам уравнивания геодезических сетей. В первую очередь поясним, что мы будем понимать под геодезической сетью в контексте данной работы.
Геодезическая сеть – это система закрепленных на поверхности земли точек (геодезических пунктов) и взаимно определенных на карте / относительно существующих объектов в плане и по высоте.
Существуют разные методы построения сетей.
При построении плановых сетей отдельные пункты сети служат исходными – их координаты должны быть известны. Координаты остальных пунктов определяют с помощью измерений, связывающих их с исходными. Плановые геодезические сети создают следующими методами.
Триангуляция – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют углы, а также длины некоторых сторон, называемых базисными сторонами (рис. 1).
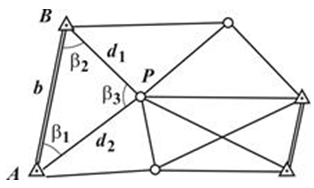
Рисунок 1.– Схема сети триангуляции
Продолжая подобным образом, вычисляют длины всех сторон сети. Если, кроме базиса b известны другие базисы (на рис. 1 базисы показаны двойной линией), то длины сторон сети можно вычислить с контролем.
Координаты пункта P определятся по формулам угловой засечки. Аналогично вычисляют координаты всех остальных пунктов.
Трилатерация – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют длины их сторон.
Если в треугольнике АВP (рис. 1) известен базис и измерены стороны , то на основе линейной засечки, можно вычислить углы треугольника.Так же вычисляют углы всех треугольников, а затем, как и в триангуляции, – координаты всех пунктов.
Полигонометрия – метод определения планового положения геодезических пунктов путем проложения ломаной линии (полигонометрического хода) или системы связанных между собой ломаных линий (сети полигонометрии), в которых измеряют углы поворота и длины сторон.
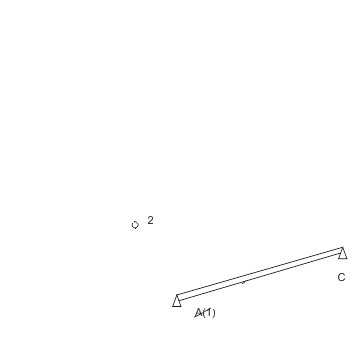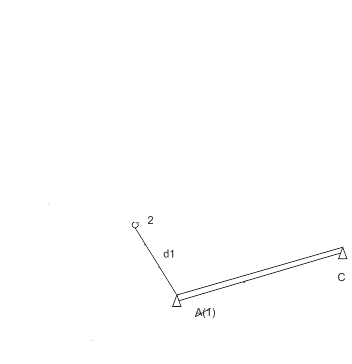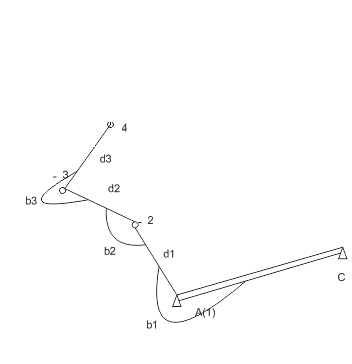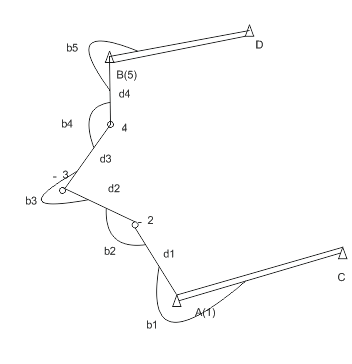
Рисунок 2.– Построение сети полигонометрии
(анимация: 5 кадров, 10 циклов повторения, 20 килобайт)
Схема полигонометрического хода показана на рис. 2 a, где A и B – исходные пункты; CA и BD – исходные направления, дирекционные углы которых известны; 1, 2, 3, 4, 5– точки (вершины) хода; b – измеренные горизонтальные углы; d – измеренные длины сторон (i = 1, 2, …).
Спутниковый метод определения координат геодезических пунктов основан на измерениях по сигналам спутников навигационных систем ГЛОНАСС (Россия) и GPS (США), выполняемых двумя (и более) наземными приемниками. По результатам измерений с высокой точностью определяют разности dx,dy,dz геоцентрических координат между пунктами. Если координаты одного из пунктов известны, то, прибавив к ним измеренные разности, находят координаты остальных пунктов. Затем координаты преобразуют в геодезические или плоские прямоугольные [9].
Каким бы методом не находились координаты пунктов то они несут в себе погрешности. Для исключения погрешностей и уравнивают геодезические сети. Для уравнивания геодезических сетей составляют с неизвестными оценками к координатам матрицы с коэффициентами весов возле неизвестных и свободными членами.
Рассмотрим два метода уравнивания геодезических измерений: метод Коши и метод наименьших квадратов.
Метод обработки геодезических измерений Коши
Рассмотрим схему уравнивания по элементам. Для простоты и без нарушения общности положим Х0=0, так что система фундаментальных уравнений примет вид.
Y = L – D = XA,
где Y – матрица свободных членов,
Х – матрица коэффициентов при неизвестных,
А – вектор столбец неизвестных.
Или, подробнее,
yr = lr – dr = [Хrj aj] (r = 1, 2,….N) (1.1)
Наблюдения предполагаются равноточными. Мы видели, что при нормальности вектора погрешностей d метод наименьших квадратов имеет некоторые экстремальные свойства среди широкого класса других методов, так что его применение в этом смысле выгодно. Но в вычислительном отношении решение системы нормальных уравнений, несмотря на обычно применяемые упрощающие приемы, все еще представляет затруднения. Поэтому иногда прибегают и к другим методам оценивая аj по наблюдениям lr ( r = 1, 2…, N) и фундаментальным уравнениям.
Составление нормальных уравнений и получение с их помощью оценок для параметров (а1 , …., а n) есть, в конечном счете, метод такого комбинирования N уравнений с погрешностями избыточной системы, чтобы в результате можно было получить разрешимую систему линейных уравнений относительно n параметров (а1 , …., а n). Таких методов может быть много, помимо метода наименьших квадратов. Хотя, как пояснено выше, они не будут уже иметь экстремальных свойств, присущих методу наименьших квадратов. Один из таких методов был предложен О. Коши.
Здесь мы изложим вкратце его содержание.
Прямой ход. Предписание О. Коши состоит в следующем. Сначала система (1) подготавливается,умножением каждого уравнения на +1 или –1 добиваются того, что х1j>0 ( j = 1,2…..N). Предположим, что это уже сделано. Далее, все уравнения складываются, так что получается
(х11 + х21…+ хN1)a1+(x12+x22+… + xN2)a2+….+(x1n+ x2n+…+ xNn)an=y1+…+yN.
Будем придерживаться обозначений Коши, полагая
x1j+x2j+…+ xNj=Sxj ( j = 1,2, …, n)
Имеем тогда
a1Sx1+…+ anSxn =Sy
В силу предыдущего, Sx1>0. Деля на Sx1, получаем:
а1 + а2 * S_(x_2 )/S_(x_2 ) +аn *S_(x_n )/(Sx_1 ) = Sy/(Sx_1 ) (1.2)
Умножаем (1.2) соответственно на х11, х12…. x1N и вычитаем из полученных N уравнений уравнение системы (1.1); тогда члены, содержащие а1, исчезают и получается система из N уравнений с (n – 1 ) неизвестными а2, ….,аn
(x12 – x11 (Sx_2)/(Sx_1 ) ) a2+… +( xnn – x11 (Sx_n)/(Sx_1 ) ) an = y1 – x11 Sy/(Sx_1 ) ,
(xN2 – xN1 (Sx_2)/(Sx_1 ) ) a2+…. +(xNn – xN1 (Sx_n)/(Sx_1 ) ) an = yN – xN1 Sy/(Sx_1 )
Далее, подготавливаем так же новую систему и производим с ней такие же операции. В конце концов, вообще говоря, получаем систему N уравнений с одним неизвестным аn
x'rnan = y'r ( r = 1, 2,…., N );
где хrn'>0 – получившиеся коэффициенты, а y'r – линейные комбинации из yq ( q = 1, 2, ….N ), получившиеся в процессе работы.
Далее, заменяем в каждом из y'r неизвестные нам yq на известные и наблюдаем yq . Результат такой замены обозначим l'r . После этого находим а'n из уравнений
a'n = (Sl_r)/(Sx_(r ) )
Обратный ход. Подставляем последнее неизвестное в матрицу (1.1), оставляем неизвестные в левой части уравнения, а известные элементы переносим в правую часть и применяем те же формулы, что и в прямом ходе, до тех пор пока не найдем все неизвестные элементы. Формируем вектор столбец из найденных неизвестных [2].
Метод обработки геодезических измерений метод наименьших квадратов
Существует два подхода к решению задачи уравнивания. Рассмотрим их по существу.
1. Возьмем треугольник, где измерены все три угла(рис.3). Следовательно, имеет место уравнение
b1+v1+b2+v2+b3+v3–180=0
где b – измеренные углы, v – поправки.
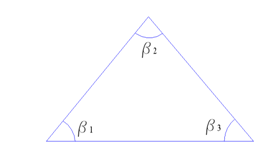
Рисунок 3.– Треугольник, где измерены все три угла
Обозначив:
b1+b2+b3–180=W
где W – невязка в треугольнике, можем записать
v1+v2+v3+W=0. (2.1)
В (2.1) v1,v2,v3 – неизвестные, а W – свободный член.
Мы получили одно уравнение с тремя неизвестными, которое имеет множество решений, т.е. система является неопределенной.
2. Возьмем систему трех нивелирных ходов с одной узловой точкой(рис.4.). Неизвестной при этом будет высота узловой точки H.
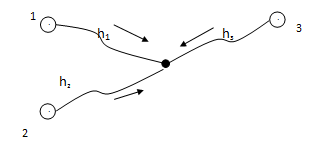
Рисунок 4 – Система трех нивелирных ходов с одной узловой точкой
Следовательно, можно записать три уравнения
H–H1–h1=v1
H–H2–h2=v2 (2.2)
H–H3–h3=v3
где Hi – высоты исходных реперов, H – высота узловой точки, hi – измеренные превышения.
Таким образом, мы имеем три уравнения с одним неизвестным Н. Следовательно, мы снова получили неопределенную систему.
Принцип наименьших квадратов и его обоснование.
Сущность решения по принципу наименьших квадратов состоит в том, что системы решаются под условием
[pvv]=min (2.3)
где р – веса измерений, т.е. под условием минимума суммы квадратов поправок, умноженных на веса измерений. В случае равноточных измерений (2.3) принимает вид:
[vv]=min
Рассмотрим решение задачи уравнивания по этому способу на примере системы (2.2).
Представим (2.2) в виде:
H–l1=v1
H–l2=v2
H–l3=v3
где li=Hi+hi(i=1,2,3), и подставим в (2.3).
f(H)=p1v1v1+p2v2v2+p3v3v3=p1(H–h1)^2+p2(H–h2)^2+p3(H–h3)^2
Чтобы найти минимум функции f(H) возьмем производную по переменным hi и приравняем ее нулю.
f'(H)=2p1(H–h1)+2p2(H–h2)+2p3(H–h3)=0
или
2H(p1+p2+p3)–2(h1p1+h2p2+h3p3)=0
В результате получим:
H=[ph]/[p] (2.4)
Выражение (2.4) представляет собой общую арифметическую средину [5].
Чтобы убедиться, что решение (2.4) действительно дает минимум (2.3), найдем вторую производную:
f'(H)=2p1+2p2+2p3=2[p]>0
Вторая производная положительна. Следовательно,
f(H)=[pvv]=min
Подведем итог:
1. Мы получили единственное решение системы (2.2). При этом оно оказалось общей арифметической срединой, что подтверждает единство принципа наименьших квадратов и принципа арифметической средины.
2. Из (2.3) и (2.4) следует, что решение (2.4) соответствует минимуму функции (2.3) и соответственно минимуму эмпирической средней квадратической погрешности единицы веса:
mm=[pvv]/(n–1)
Следовательно, вес определяемой величины, равный:
PH=c[p]/mm
где с – произвольная положительная постоянная.
При любых значениях с, [p] PH будет максимальным [6].
Поэтому решение, найденное способом наименьших квадратов соответствует наибольшему весу определяемой величины.
Применительно к двум подходам, сформулированных нами в 2.2 в виде уравнений (2.2) и (2.1) существует два способа уравнивания:
1. Параметрический способ
2. Способ уравнивания измеренных величин, связанных условиями [3].
Параметрический способ уравнивания.
Пусть для определения значений неизвестных x,y,z,…t выполнены равноточные независимые измерения L1,L2,..,Ln. Общее число неизвестных t , общее число измерений n. При чем n>t, т.е. система неопределенная.
Неизвестными могут быть координаты пунктов, высоты реперов и другие величины, значения которых необходимо определить.
Измеряемыми величинами в этом случае будут горизонтальные направления, горизонтальные или вертикальные углы, длины линий, превышения и т.д.
Между неизвестными x,y,z…t и измеренными величинами Li существуют точные математические зависимости, которые в общем виде можно представить:
fi(x,y,x,..,t)=Li+Vi (2.5)
где Vi – поправки к измеренным значениям Li .
На основании (2.5) сможем записать систему уравнений поправок в общем виде:
f1(x,y,x,..,t)–L1=V1
f2(x,y,x,..,t)–L2=V2 (2.6)
....................
fn(x,y,x,..,t)–Ln=Vn
Перед уравниванием уравнения (2.6) необходимо привести к линейному виду. Для этого введем приближенные значения неизвестных x0,y0,z0,..,t0 и поправки к этим приближенным значениям dx,dy,dz,..,dt т.е.
x=x0+dx
y=y0+dy
z=z0+dz (2.7)
.......
t=t0+dt
Подставим (2.7) в (2.6)
fi(x0+dx,yo+dy,z0+dz,..,to+dt)–Li=Vi (2.6a)
Разложим функцию fi в ряд Тейлора, ограничиваясь только первыми степенями поправок. В результате получим:
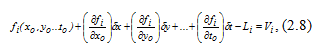
Рисунок 5.–Разложение в ряд Тейлора функции fi
где i=(1,2,..,n)
Введем обозначения:
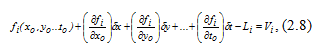
Рисунок 5.–Разложение в ряд Тейлора функции fi

Рисунок 6.–Обозначения
С учетом (2.7), (2.8), и (2.9) система уравнений поправок (2.6) принимает вид:
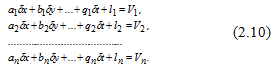
Рисунок 7.–Система уравнений поправок
Общее число уравнений поправок равно числу измерений n [8].
Возьмем систему уравнений поправок в линейном виде. Чтобы выкладки были не такими громоздкими, ограничимся только тремя неизвестными, имея ввиду, что полученные результаты можно будет распространить на любое число неизвестных. Итак,
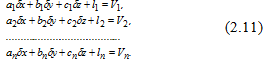
Рисунок 8.–Система уравнений поправок с тремя неизвесными
Число уравнений больше числа неизвестных. Число уравнений n, число неизвестных 3. Число избыточных измерений r = n – 3, а потому система (2.11) не имеет единственного решения.
Найдем для этой системы минимум [vv] . Возведем в квадрат левые и правые части уравнений поправок (2.11), а результаты сложим.
![Нахождение [vv] Нахождение [vv]](images/9.png)
Рисунок 9.–Нахождение [vv]
Чтобы найти минимум [vv] , возьмем от функции (2.12) частные производные по неизвестным dx,dz,dz и приравняем их нулю
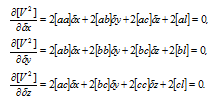
Рисунок 10.–Частные производные по неизвестным
Сократив на общий множитель 2, получим
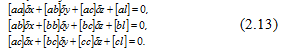
Рисунок 11.–Частные производные по неизвестным сокращенные на 2
В системе (2.13) число неизвестных равно числу уравнений. Такая система имеет единственное решение. Вот почему уравнения (2.13) принято называть нормальными уравнениями.
В этой системе коэффициенты при неизвестных, расположенные по главной диагонали, называют квадратичными, которые всегда положительны [4]. Коэффициенты при неизвестных, расположенные симметрично относительно главной диагонали, попарно равны между собой, т.е. система (2.13) симметрична. Решив эту систему, находим неизвестные dx,dy,dz. Подставляем неизвестные в (2.11) и находим поправки.
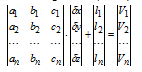
Рисунок 12.–Матричный вид системы уравнений поправок
или сокращенно:
ad+l=V (2.14)
Матрица a имеет размер nxt,d–tx1,V–nx1.
Транспонируем матрицу a и умножаем ее слева почленно на выражение (2.14).
a^Tad+a^Tl=a^TV (2.15)
Рассмотрим произведения матриц, входящих в (2.15).
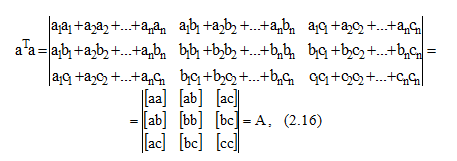
Рисунок 13.–Произведение матриц a^T*a
т.е. мы получили матрицу коэффициентов нормальных уравнений (2.13) [10].
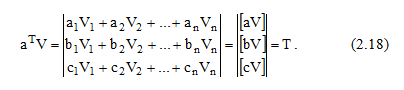
Рисунок 14.–Произведение матриц a^T*V
Принимая во внимание (2.16) и (2.17), приходим к выводу, что левая часть выражения (2.11) есть не что иное, как система нормальных уравнений (2.9) в матричной форме. В (2.13) и (2.15) левые части равны [1]. Следовательно, должны быть равны правые. Поэтому можем записать
[aV]=0;[bV]=0;[cV]=0 (2.19)
Система нормальных уравнений принимает вид:
Ad+alfa=0 (2.20)
Так как уравнения поправок (2.16) независимы друг от друга, матрица A неособенная. Следовательно, для решения уравнения (2.20) необходимо и достаточно умножить его слева на матрицу A^–1, обратную матрице A . В результате будем иметь:
d=–A^–1*alfa (2.21)
Подведем итог. Уравнивание параметрическим способом осуществляется в такой последовательности:
1. Подсчитываем количество определяемых неизвестных t, подсчитываем число независимых измерений n и определяем число избыточных измерений r=n–t. Если n=t, r=0, то задача уравнивания измеренных величин не возникает.
2. Используя только необходимые измерения, определяем тем или иным способом приближенные значения неизвестных x0,y0,z0,..,t0.
3. Составляем уравнения поправок в общем виде (2.7), приводим их к линейному виду (2.11). В результате получаем коэффициенты уравнений поправок a,b,c,..,q.
4. Вычисляем свободные члены уравнений поправок по формуле (2.10).
5. Составляем матрицу коэффициентов уравнений поправок и матрицу- столбец свободных членов l. Размер матрицы a(nxt), а матрицы l(nx1). Составляем уравнения поправок в матричной форме (2.16).
6. Транспонируем матрицу a.
7. Умножаем матричное уравнение (2.16) слева на матрицу a^T. В результате получаем систему нормальных уравнений (2.15), представленную в матричной форме (2.21).
8. Находим матрицу A^–1, обратную матрице коэффициентов нормальных уравнений A. Размер той и другой матрицы txt.
9. Умножаем уравнение (2.21) слева на матрицу A^–1. В результате получаем вектор-столбец поправок d. Размер матрицы tx1.
10. Вычисляем по формуле (2.8) уравненные значения неизвестных x,y,...,t.
11. Подставляем вектор-столбец d в уравнение (2.15), умножаем и складываем матрицы. В результате получаем матрицу-столбец поправок к измеренным величинам V . Размер матрицы nx1 . Вычисляем уравненные значения Li+Vi.
12. Оцениваем точность полученных в результате уравнивания неизвестных величин x,y,..,t [7].
Выводы
При выполнении анализа методов была проанализирована нормативная литература и различные интернет источники описывающие наиболее рациональное применение того или иного метода уравнивания.
На момент написания реферата было написана мною программа в MathCAD по реализации уравнивания геодезических сетей методом Коши, выполнилось уравнивание равноточных и неравноточных измерений и сделан анализ по сравнению результатов рассчитанных по методу Коши и методу наименьших квадратов.
На основании полученных данных можем сделать вывод, что использование метода наименьших квадратов является предпочтительнее для выполнения уравнивания геодезических сетей, т. к. вычисляется оценка с большей точностью.
Планируется проведения дальнейших исследований.
На момент написания реферата, Магистерская работа еще не завершена. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после декабря 2015 года.
Список источников
- Метод наименьших квадратов. – [Электронный ресурс] –http://geodesy-book.narod.ru/Numerical_methods/05.pdf
- Метод наименьших квадратов и основы теории обработки наблюдений/ Ю. В. Линник. –М.:Государственное издательство физико-математической литературы, 1958 – с. 338.
- Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений: Учебное пособие для вузов.– М.:Недра, 1984, 352 с.
- Теория матриц./Ланкастер П. – М.: Наука, 1982. – 272 с.
- Чернова Н.И. Теория вероятностей: Учеб. пособие/ Сиб-ГУТИ. Новосибирск, 2007. – 128с.
- Губанов В.С. Обобщенный метод наименьших квадратов. Теория и применение в астрометрии. – М.: Наука, 1997. – 319с.
- Чеботарев А.С. Способ наименьших квадратов. – М.: Геодезический факультет и военно-геодезическое отделение Московского межевого института, Издательство Московского высшего технического училища, 1928. – 475 с.
- Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.: Физматгиз, 1963, 734 с.
- Методы и приборы высокоточных геодезических измерений в строительстве./ Под редакцией В.Д. Большакова. – М.: Недра, 1976.– 335 с.
- Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: – Наука. Главная редакция физико-математической литературы. 1984. – 320 с.
