ДонНТУ   Портал магистров

Геометрия Лобачевского как пример аксиоматической теории

Когда-то Лобачевский думал,
Кутаясь в пальто,
Как мир прямолинеен,
Видно, что-то здесь не то.
Но он вгляделся пристальней
В безоблачную высь,
А там все параллельные его пересеклись.

История своего увлечения

Математика — мой любимый школьный предмет с первого класса. Мне нравится решать примеры и задачи, находить ответы на логические вопросы.

Математика нужна абсолютно во всех сферах жизни. Каждый день мы пользуемся простыми арифметическими действиями, чтобы делать покупки, чтобы планировать свое время. В каждой профессии так или иначе используются математические расчеты, даже если это не заметно с первого взгляда. Для многих специальностей нужно глубокое знание математики, например, для инженеров, программистов, физиков.

Математика — это основа для всех наук. Невозможно изучать физику, химию, биологию, если не умеешь делать необходимые расчеты. Чтобы добиться успеха и получить хорошее образование, необходимо хорошо знать математику. Эта наука двигает мир вперед, помогает развивать науку. Это основа для научно-технического прогресса, основа для нашего нового, будущего мира.

На уроках геометрии в 7-м классе я познакомилась с аксиомой параллельности прямых: в плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.

Углублённо изучая геометрию, я узнала, что эта аксиома верна только для геометрии Евклида в пространстве, которое тоже называется Евклидовым. И, что существуют другие геометрии и другие пространства, где эта аксиома не выполняется. Одну из таких геометрий придумал Николай Иванович Лобачевский.

Я выбрала тему Геометрия Лобачевского как пример аксиоматической теории по нескольким причинам:

  1. Теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир.
  2. Это интересный, необычный и прогрессивный раздел современной геометрии.
  3. Она дает материал для размышлений — в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением.

Вначале геометрия Лобачевского считалась непригодной к практическому применению, так как пространство, в котором мы живем, не соответствует пространству, описываемому этой геометрией. Однако законы, выведенные Лобачевским, вскоре нашли практическое применение.

За последние 15 лет значение геометрии Лобачевского еще более возросло благодаря работам американского математика Тёрстона (лауреата Филдсовской медали 1983 г.), установившего ее связь с топологией трехмерных многообразий. Десятки работ ежегодно публикуются в этой области. Современные исследования все больше требуют владения геометрией Лобачевского [1].

Геометрия как раздел математики о пространстве мира

Геометрия — важный раздел математики, изучающий пространственные структуры и отношения. Она наглядно позволяет отобразить разные закономерности и геометрические объекты. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур.

Например, название фигуры трапеция происходит от греческого слова трапезион (столик), от которого произошли также слово трапеза и другие родственные слова.

Рисунок 1 — Пример трапеции

Рисунок 1 — Пример трапеции

От греческого слова конос (сосновая шишка) произошло название конус, а термин линия возник от латинского линум (льняная нить). И факты геометрии сначала имели опытное происхождение [2].

Рисунок 2 — Пример конуса

Рисунок 2 — Пример конуса

Рисунок 3 — Примеры линий

Рисунок 3 — Примеры линий

В геометрии можно выделить следующие разделы:

Понятие пространства мира

Корни развития представления о пространстве уходят в немецкую философию. Если Ньютон довел до логического завершения материалистически-атомистическую тенденцию развития представлений о пространстве, то идеалистическую трактовку пространства в наиболее развернутой форме дал Гегель. Пространство, считает Гегель, находится в неразрывной диалектической взаимосвязи со временем, движением и материей: лишь в движении пространство и время действительны, но точно так же, как нет движения без материи, так не существует материи без движения.

Гегель утверждает: ...Пространство и время непрерывны в самих себе, и движущееся тело одновременно находится и не находится в одном и том же месте, т.е. одновременно находится в другом месте, и точно так же одна и та же временная точка существует и вместе с тем не существует, т.е. есть вместе с тем другая точка. Или: Две точки сливаются в единую точку, и в то время, когда они есть в одном, они также не есть в одном. Движение и состоит именно в том, что тело находится в одном месте и одновременно в другом месте, причем столь же верно, что оно находится не в другом, а именно в данном месте [4].

Евклидова геометрия, представляет собой геометрическую теорию, основанную на системе аксиом, впервые изложенной в Началах Евклида (III век до н. э.). Евклидова геометрия — привычная геометрия, изучаемая в школе. Обычно относится к двум или трём измерениям, хотя можно говорить о многомерном евклидовом пространстве.

В Началах собраны все геометрические сведения, полученные трудами десятков математиков античности, живших до Евклида. Этот труд, состоящий из тридцати томов, на два тысячелетия стал единственным учебником, по которому можно было изучить геометрию. И Начала прекрасно описывают пространство, в котором мы живем, благодаря чему эту геометрию (как и пространство) назвали Евклидовой [5].

Каждая из книг начинается определением понятий (точка, линия, плоскость, фигура и т. д.), которые в ней используются, а затем на основе небольшого числа основных положений, принимаемых без доказательства, строится вся система геометрии [6].

Вспомним три основные аксиомы евклидовой геометрии:

  1. Между двумя точками можно провести одну и только одну прямую.
  2. Эта прямая есть кратчайшее расстояние между точками.
  3. Через любую точку, лежащую вне прямой, можно провести одну и только одну прямую, параллельную данной.

Практика подсказывает, что эти аксиомы совершенно очевидны и не требуют специального геометрического либо какого-то другого математического доказательства.

Возникновение геометрии Лобачевского

При исследовании Начал Евклида делались попытки уточнить основные положения геометрии. Но очень немногие ставили задачу пополнения списка аксиом или постулатов. Напротив, их количество (в большинстве случаев) пытались уменьшить.

В этих исследованиях особое место занимают исследования, связанные с V постулатом Евклида [7].

V постулат: если на плоскости при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180°, то эти прямые при достаточном продолжении пересекаются, и притом с той стороны, с которой эта сумма меньше 180° (через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её) (рисунок 4).

Рисунок 4 — Внутренние односторонние углы

Рисунок 4 — Внутренние односторонние углы

(Анимация Размер: 100 Кб; Количество кадров: 14; Количество повторов: неограничено; Задержка: 0.75 сек)

Вопрос о V постулате Евклида, занимавший геометров более двух тысячелетий, был решен Лобачевским. Это решение сводится к тому, что постулат не может быть доказан на основе других посылок евклидовой геометрии и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий. Лобачевский сделал об этом сообщение в 1826, а в 1829–30 напечатал работу О началах геометрии с изложением своей теории. В 1832 была опубликована работа венгерского математика Яноша Больяй аналогичного содержания. Как выяснилось впоследствии, немецкий математик Карл Гаусс также пришёл к мысли о возможности существования непротиворечивой неевклидовой геометрии, но скрывал её, опасаясь быть непонятым [8].

Сущность геометрии Лобачевского

Основная идея геометрии Лобачевского заключается в новой формулировке аксиомы параллельности, противоположной евклидовой: к данной прямой через данную точку, лежащую вне ее, можно провести по меньшей мере две прямые так, что они не пересекают данную прямую. Очевидно, что любая прямая, расположенная между этими прямыми и проходящая через данную точку, также не пересечет данную прямую. Таким образом, через данную точку можно провести сколько угодно прямых, параллельных данной. Все другие аксиомы Евклида сохраняются. Из этого Лобачевский выводит ряд теорем, которые не противоречат друг другу, и строит логически непротиворечивую геометрию, которая значительно отличается от евклидовой и кажется весьма странной. Так, сумма углов треугольника всегда меньше 180°; невозможно построить фигуру, подобную данной, но имеющую другие размеры; расстояние между двумя прямыми в одном направлении асимптотически увеличивается, а в другом, противоположном, асимптотически уменьшается; угол параллельности меняется в зависимости от расстояния от точки, через которую проводится параллельная линия, до данной линии и т.д. [9].

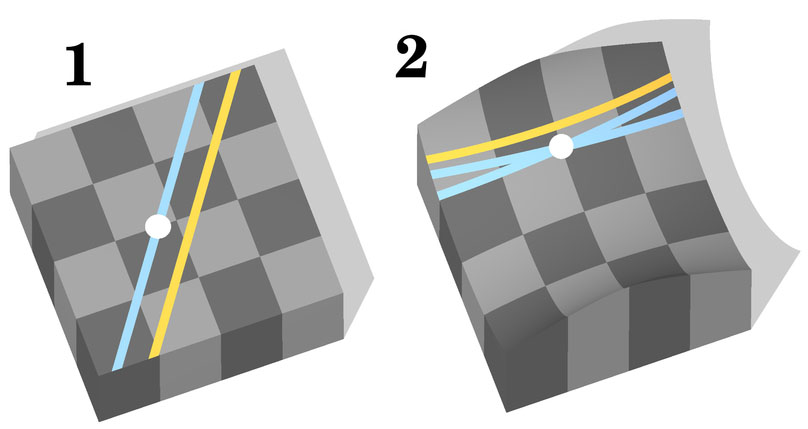
Рисунок 5 — Евклидова геометрия (1) и геометрия Лобачевского (2)

Рисунок 5 — Евклидова геометрия (1) и геометрия Лобачевского (2)

Аксиома Лобачевского является точным отрицанием аксиомы Евклида (при выполнении всех остальных аксиом), так как случай, когда через точку, не лежащую на данной прямой, не проходят ни одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её, исключается в силу остальных аксиом (аксиомы абсолютной геометрии).

Можно построить двумерный образ геометрии Лобачевского путем вращения трактрисы вокруг оси OY как оси вращения. Полученная поверхность носит название псевдосферы. На такой поверхности кратчайшей линией между двумя точками будет кривая, называемая геодезической. Эта кривая и соответствует прямой Лобачевского. При передвижении фигуры по поверхности будет меняться кривизна фигуры, но сохранятся углы, отрезки и величина площади [4].

Чтобы понять это, необходимо сделать одно очень важное уточнение: геометрия Лобачевского описывает не плоское пространство, как это делает геометрия Евклида, а оперирует понятиями гиперболического пространства. В геометрии Лобачевского пространство не плоско, оно имеет некоторую отрицательную кривизну. Представить это достаточно сложно, но хорошей моделью такого пространства являются геометрические тела, похожие на воронку и седло (рисунок 6). И все сказанное выше относится именно к поверхностям этих фигур [5].

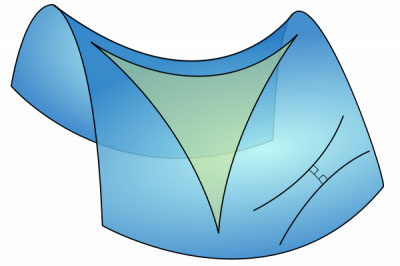
Рисунок 6 — Пример модели пространства Лобачевского

Рисунок 6 — Пример модели пространства Лобачевского

Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере [10]. Пример модели псевдосферы показан на рисунке 7.

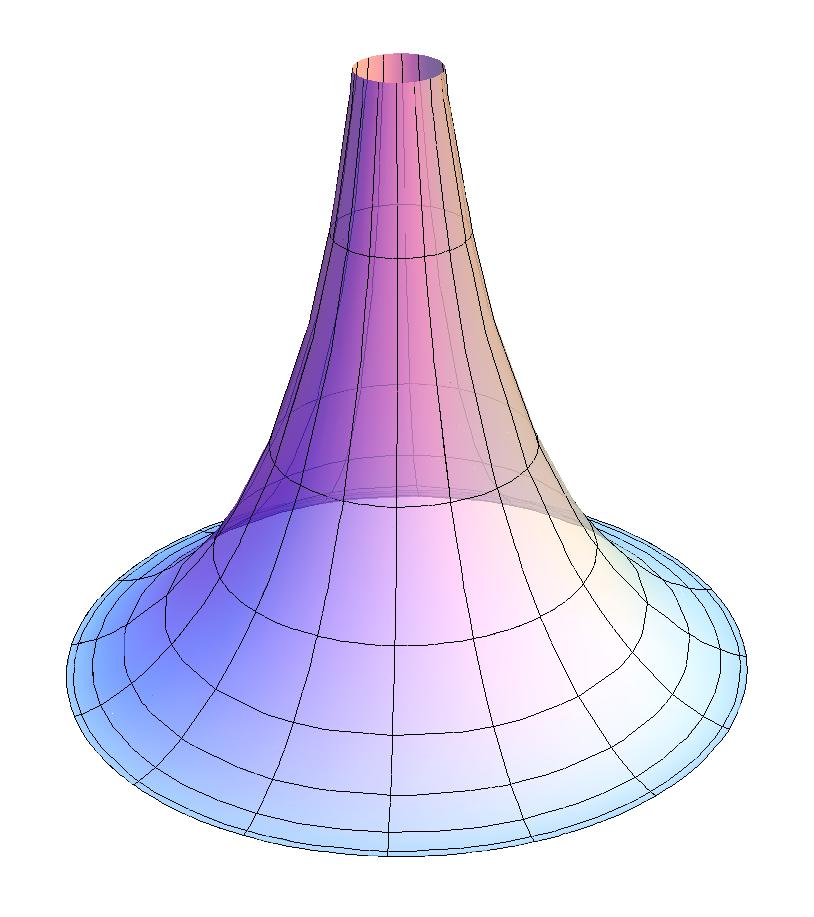
Рисунок 7 — Пример модели псевдосферы

Рисунок 7 — Пример модели псевдосферы

Приведём несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским:

  1. В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому как прямой угол выделен своими свойствами.
  2. Сумма углов всякого треугольника меньше π и может быть сколь угодно близкой к нулю (разница между 180° и суммой углов треугольника ABC в геометрии Лобачевского положительна — её называют дефектом этого треугольника)
  3. Через точку, не лежащую на данной прямой , проходит бесконечно много прямых, не пересекающих прямую и находящихся с ней в одной плоскости.
  4. Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.
  5. Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.
  6. Длина окружности не пропорциональна радиусу, а растет быстрее.

Остальные аксиомы Лобачевский оставил без изменения и на основе новой системы построил новую геометрию, отличную от евклидовой.

Заслуга Лобачевского состоит в том, что он не только высказал идею, но действительно построил и всесторонне развил новую геометрию, логически столь же совершенную и богатую выводами, как евклидова, несмотря на её несоответствие обычным наглядным представлениям. Лобачевский рассматривал свою геометрию как возможную теорию пространственных отношений [11].

Создание геометрии Лобачевского оказало огромное влияние на все науки. Ее результаты используются внутри математики – в теории чисел, в математическом анализе. В частности, сам Лобачевский с помощью своей геометрии вычислили около 200 интегралов. Но наиболее широкое применение она нашла в современной физике — общей и специальной теории относительности, в квантовой механике и других областях [1].

Непреходящее значение открытия геометрии Лобачевского для науки состоит в том, что оно разрушило приобретенные веками традиционные взгляды на окружающий мир, вывело ученых из узких рамок созданных ими стереотипов мышления. Они стали более восприимчивы к новым неожиданным научным открытиям.

Применение геометрии Лобачевского

Геометрия Лобачевского продолжает разрабатываться многими геометрами; в ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей и т. п. В целом Лобачевского геометрия является обширной областью исследования, подобно геометрии Евклида.

Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов. Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой геометрии чисел [12].

Спутниковые навигационные системы (GPS и ГЛОНАСС) состоят из двух частей: орбитальная группировка из 24–29 спутников, равномерно расположенных вокруг Земли, и управленческий сегмент на Земле, обеспечивающий синхронизацию времени на спутниках и использование ими единой системы координат. На спутниках установлены очень точные атомные часы, а в приемниках (GPS-навигаторах) обычные, кварцевые. Для работы навигаторов нужны очень точные часы на спутниках орбитальной группировки. Ход часов в этих условиях изменяется благодаря известному в специальной теории относительности эффекту: из-за большой скорости спутника часы на орбите идут иначе, чем такие же часы на Земле. Но кроме этого, есть и специфический для общей теории относительности эффект такого рода, связанный как раз с неевклидовой геометрией пространства-времени. И если в какойто момент отключить учёт этих эффектов, то уже за сутки работы в показаниях навигационный системы накопится ошибка порядка 10 км.

Формулы геометрии Лобачевского также используются в физике высоких энергий, а именно, в расчетах ускорителей заряженных частиц. Гиперболические пространства встречаются и в самой природе. Геометрия Лобачевского проглядывается в структурах кораллов, в организации клеточных структур у растении, в архитектуре, у некоторых цветков и так далее [13].

Список источников

  1. А.С. Гребеньков. Поиск текстов в Интернете на основе базы цитат. X Всероссийская объединенная конференция, с. 258-260 — [Электронный ресурс]. — Режим доступа: http://ict.edu.ru/vconf/files/7877.pdf
  2. Кристофер Д. Маннинг, Прабхакар Рагхаван, Хайнрих Шютце. Введение в информационный поиск — [Электронный ресурс]. — Режим доступа: https://www.ozon.ru/context/detail/id/5497130/
  3. Хараламбос Марманис, Дмитрий Бабенко. Алгоритмы интеллектуального Интернета. Передовые методики сбора, анализа и обработки данных — [Электронный ресурс]. — Режим доступа: https://www.ozon.ru/context/detail/id/6753996/
  4. Г.С. Осипов, И.А. Тихомиров, И.В. Смирнов. Интеллектуальный поиск в глобальных и локальных вычислительных сетях, и базах данных. Программные системы: теория и приложения. Переславль-Залесский, 2004, 21-34 — [Электронный ресурс]. — Режим доступа: http://docplayer.ru/27455876-Intellektualnyy-poisk-v-globalnyh-i-lokalnyh-vychislitelnyh-setyah-i-bazah-dannyh.html
  5. Г.С. Осипов, И.А. Тихомиров, И.В. Смирнов. Искусственный интеллект и принятие решений, Реляционно-ситуационный метод поиска и анализа текстов и его приложения, 2008, №2, 3-10 — [Электронный ресурс]. — Режим доступа: http://docplayer.ru/29580361-Relyacionno-situacionnyy-metod-poiska-i-analiza-tekstov-i-ego-prilozheniya.html
  6. Ландэ Д.В., Снарский А.А., Безсуднов И.В. Интернетика. Навигация в сложных сетях. Модели и алгоритмы — [Электронный ресурс]. — Режим доступа: http://poiskbook.kiev.ua/art/internetica/
  7. Ландэ Д.В., Снарский А.А. Моделирование сложных сетей — [Электронный ресурс]. — Режим доступа: http://freescb.info/sites/freescb.info/files/mss-new.pdf
  8. А.Г. Додонов, Д.В. Ландэ, В.Г. Путятин. Компьютерные сети и аналитические исследования — [Электронный ресурс]. — Режим доступа: http://dwl.kiev.ua/art/ksai/an-book.pdf
  9. Каламитра Марина Викторовна. Метапоисковая система Дворцы Крыма — [Электронный ресурс]. — Режим доступа: http://masters.donntu.ru/2013/fknt/kalamitra/ind/index.htm
  10. Саркисова И.О. Автоматизация поиска неиндексируемых ресурсов в распределенных компьютерных сетях — [Электронный ресурс]. — Режим доступа: http://magazine.stankin.ru/arch/n_10/14/index.html.
  11. Архитектура метапоисковых систем — [Электронный ресурс]. — Режим доступа: http://citforum.ru/internet/search/metaping.shtml
  12. Мета-поисковые системы — [Электронный ресурс]. — Режим доступа: http://catalysis.ru/link/index.php?ID=12&SECTION_ID=54
  13. Мета-поисковые системы — [Электронный ресурс]. — Режим доступа: http://www.vsepoisk.ru/2009/07/blog-post_23.html
  14. Метапоисковые системы: принципы работы, опыты кластеризации поисковых результатов — [Электронный ресурс]. — Режим доступа: http://life-prog.ru/2_10898_metapoiskovie-sistemi-printsipi-raboti-opiti-klasterizatsii-poiskovih-rezultatov.html
  15. Метапоисковые системы — [Электронный ресурс]. — Режим доступа: https://studopedia.org/11-95698.html
  16. Шпаргалка по метапоисковым системам — [Электронный ресурс]. — Режим доступа: http://internetno.net/category/shpargalki/meta-search/
  17. Серёженко О.А., Коломойцева И.А. Применение мета-поиска к решению задач поиска цитат // Программная инженерия: методы и технологии разработки информационно-вычислительных систем (ПИИВС-2016): сборник научных трудов I научно-практической конференции (студенческая секция). 16-17 ноября 2016 г. — Донецк, ГОУ ВПО Донецкий национальный технический университет, 2016. — с. 194-200.
На верх