Реферат по теме выпускной работы

Содержание

• Введение
• 1. Актуальность темы
• 2. Цель и задачи исследования, планируемые результаты
• 3. Обзор исследований и разработок
• 3.1 Обзор международных источников
• 3.2 Обзор национальных источников
• 3.3 Обзор локальных источников
• 4. Пример плоского раскроя
• Выводы
• Список источников

Введение

Проблема экономии ресурсов является актуальной и современной для всех сфер человеческой деятельности как в настоящем, так и в обозримом будущем. При решении задачи промышленного раскроя (компоновки) важным является создание карт раскроя, при которых получается максимальный комплект заготовок деталей и, следовательно, достигается минимизация отходов материалов.

Задачи такого рода объединены под термином «задача раскроя-упаковки» и относятся к классу NP-трудных (Nondeterministic polynomial), т.е. переборная вычислительная сложность задачи не позволяет находить точное решение для достаточного количества геометрических объектов за приемлемое время.

1. Актуальность темы

Разработка программного обеспечения оптимального раскроя востребована и актуальна в различных сферах автоматизированного проектирования и планирования. Разработка и использование эффективных методов решения этих задач имеет не только практическую, но и научную ценность, так как в основе лежат комбинаторные оптимизационные модели. Использование современных средств разработки и визуализации позволяет повысить качество программного обеспечения и расширить круг решаемых задач.

В настоящее время в мире происходит серьезная перестройка ряда отраслей промышленности, идут интеграционные процессы, связанные с укрупнением промышленного производства и созданием групп предприятий. Обострение конкуренции среди промышленных предприятий и необходимость снижения себестоимости производимой продукции требуют повышения эффективности производства, более рационального расходования имеющихся в его распоряжении финансовых и материальных средств и ресурсов, повышения производительности труда за счет повышения качества планирования производства, его реструктуризации и модернизации, освоения новой, более совершенной и конкурентоспособной продукции.

2. Цель и задачи исследования, планируемые результаты

Целью исследования является разработка математических моделей алгоритмов раскроя, разработка новых алгоритмов и методов решения, модификация (при необходимости) существующих, программная реализация подсистем комплекса, визуализация, оценка эффективности разработанного ПО и используемых алгоритмов, исследование работоспособности, которые смогут минимизировать отходы на производстве. На основании полученных методов необходимо создать алгоритмы для программного комплекса, результатами работы которых будут повышение эффективности создания карт раскроя.

Основные задачи исследования:

1. Анализ существующего программного обеспечения оптимального раскроя.
2. Анализ классов задач плоского раскроя и их оценка с точки зрения вычислительной сложности.
3. Разработка математических моделей решаемых задач.
4. Разработка алгоритмов и методов решения.
5. Визуализация исходных данных и результатов.
6. Оценка эффективности разработанного ПО и используемых алгоритмов, исследование работоспособности.
7. Документирование, создание программного комплекса и оценка работы.

Объект исследования: оптимизация производства.

Предмет исследования: методы и алгоритмы создания карт оптимального плоского раскроя.

В рамках магистерской работы планируется получение актуальных научных результатов по следующим направлениям:

1. Создание карт раскроя.
2. Исследование существующих алгоритмов раскроя.
3. Разработка собственных алгоритмов.
4. Оценка эффективности алгоритмов.

В качестве практических результатов планируется разработка программного комплекса, способного генерировать карты раскроя, вычислять эффективность алгоритмов.

3. Обзор исследований и разработок

Поскольку вопросы оптимизации являются неотъемлимой частью цифровых систем, то проблемы их анализа, минимизации и реализации были широко исследованы как американскими, европейскими, японскими учеными, так и отечественными специалистами.

  3.1 Обзор международных источников

Обзор работ по проблеме упаковки/размещения трехмерных геометрических объектов (ГО), которая востребована во многих областях человеческой деятельности (компоновка [1], упаковка грузов, раскрой кристаллов и т.д.), позволяет сделать вывод, что сложность решения рассматриваемой задачи обуславливает отсутствие эффективных алгоритмов её решения. Большинство работ сводится к размещению простых геометрических фигур (параллелепипедов, цилиндров, сфер и т.д.). Поэтому поиск новых подходов и алгоритмов для решения задачи размещения трехмерных ГО остается актуальным [2, 3, 4, 5].

  3.2 Обзор национальных источников

В работе М. А. Мясогутова [6] приведен алгоритм решения NP-трудной задачи упаковки невыпуклых многогранников в прямоугольный параллелепипед минимальной высоты, позволяющий получать результаты, превосходящие известные методы решения этой проблемы, и базирующийся на построении годографа функции плотного размещения для моделирования условий взаимного непересечения многогранников. В дальнейшем предполагается проведение углубленного вычислительного эксперимента по исследованию эффективности применения различных методов оптимизации при реализации внешней (оптимизационной) процедуры.

В своей статье Р. Т. Мурзакаев, В. С. Шилов и А. В. Буркова [7] проанализировали основные методы решения задачи фигурной нерегулярной укладки плоских деталей.

  3.3 Обзор локальных источников

В Донецкой национальном техническом университете разрабатывались научные статьи, посвященные оптимизации алгоритмов раскроя. В статье Шатат Ахмед Фуад [8] приводится пример гильотинного раскроя рулонных материалов.

4. Реализация алгоритма раскроя

  4.1 Общая постановка проблемы

В условиях современного мелкосерийного производства занимающегося изготовлением деталей из листового (рулонного) материала, достаточно остро стоит вопрос об оптимальном раскрое данного материала, так как правильный раскрой, в первую очередь, позволит сократить материальные затраты ресурсов и соответственно снизить себестоимость готовой продукции, повысить ее конкурентные кондиции и в конечном итоге получить большую прибыль. Итак, среди существующих раскроев можно выделить следующие: фигурный, косоугольный, прямоугольный. Фигурный раскрой размещает на карте детали непрямоугольной формы, косоугольный – прямоугольной формы, но расположенным не параллельно граням материала. Прямоугольный раскрой работает только с деталями прямоугольной формы, которые на карте раскроя располагаются со следующими ограничениями:

• ребра предметов параллельны ребрам полосы;
  
• предметы не пересекаются друг с другом;
  
• предметы не пересекаются со сторонами полосы;
  

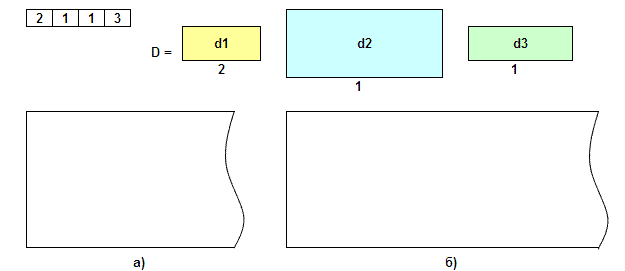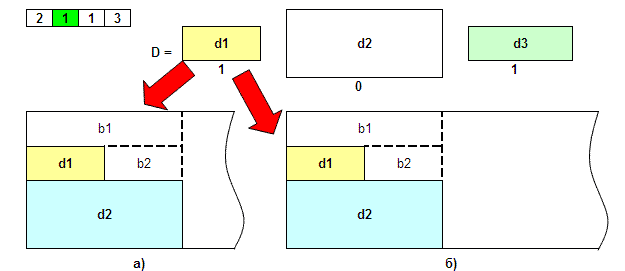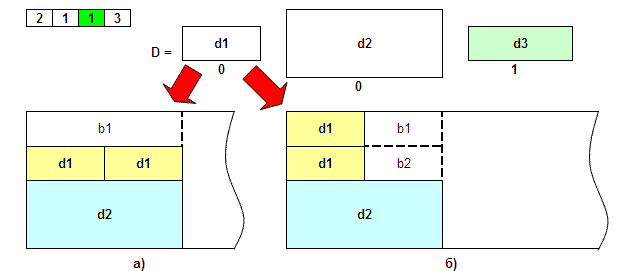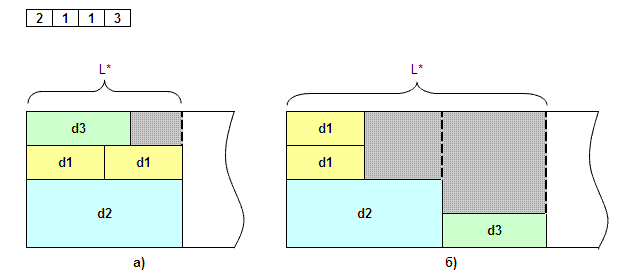
Также прямоугольный раскрой может быть гильотинный (рис. 1а) и негильотинный (рис. 1б). Под гильотинным понимается раскрой, реализуемый последовательностью сквозных резов, параллельных кромкам материала (рис. 1а) [9]. На рис. 1б представлен негильотинный раскрой. Раскрой, о котором пойдет речь в данной статье будет прямоугольным, гильотинным и рулонным (размер полосы: ширина = const, длина = ∞ ).

Рисунок 1 - Прямоугольный раскрой

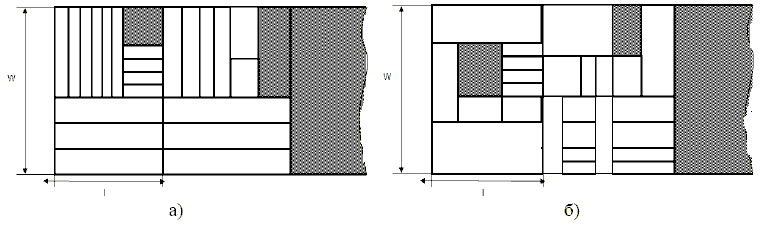
  4.2 Постановка задачи

Поставленную задачу, которую необходимо решить в данной работе можно сформулировать следующим образом: имеется исходный материал D = {W, L} полубесконечной прямоугольной формы. Ширина имеет фиксированный размер W = const, а длина является условно бесконечной L ≈ ∞, а также векторы типоразмерностей прямоугольных деталей d = {d₁(w₁, l₁), d₂(w₂, l₂), … , d_i(w_i, l_i), … , d_k-1(w_k-1, l_k-1), d_k(w_k, l_k)} и их количество n = {n₁, n₂, … , n_i, … ,n_k-1, n_k}. Необходимо оптимально расположить детали d на поверхности материала D с соблюдением следующих условий:

• w_i параллельно или перпендикулярно (если предполагается поворот детали на 90°) W – условие прямоугольности резов;
  
• d_i ∩ d_j = {l; ∅}, где l – отрезок – детали не пересекаются друг с другом;
  
• d_i ∩ D = d_i – детали не выходят за пределы исходного материала;
  

Предполагается использование нескольких критериев оценки оптимальности размещения деталей, имеющих различный приоритет. То есть, при выполнении оптимума первого приоритета отбирается размещение по оптимуму следующего приоритета и т.д. Для данной постановки, опишем оптимумы в соответствии с их приоритетами:

1. Оптимальными будут такие последовательности P_i размещения деталей, при которых L'(P _i) > min, где L' – длина использованного исходного материала L.
2. Из отобранных по первому приоритету оптимальными будут такие последовательности K_i, при которых K(P_i) > min, где K' – количество необходимых резов.
3. Из отобранных по второму приоритету оптимальными будут такие последовательности O_i, при которых O(K_i) > min, где O – площадь полученных отходов.

Следует отметить, что в постановку задачи входит так же дополнительные условия производственной оптимизации, которые могут включать:

• возможность увеличения типоразмера деталей в заданных пределах для минимизации количества отходов и резов;
  
• ограничение на количество деталей в подкорзине (одна или несколько);
  
• возможность поворотов деталей на 90°;
  
• учет величины кромки, как для деталей, так и для материала.

  4.3 Возможные методы решения.

Задача раскроя-упаковки принадлежит к классу NP-трудных задач, тоесть для ее точного решения не существует алгоритма полиномиальной сложности. Более того, рассматриваемая задача является NP-трудной в сильном смысле, так как содержит NP-трудную задачу в качестве подзадачи. До сих пор не разработано эффективных и достаточно точных способов расчета нижних границ для данной задачи, позволяющих определить достижение оптимума. Таким образом, точные алгоритмы сводятся к полному перебору вариантов. В связи с этим, использование точных алгоритмов для решения задачи раскроя-упаковки часто оказывается нецелесообразным и невозможным по причине больших затрат времени. Поэтому большое значение уделяется разработке и исследованию эвристических методов оптимизации [10].

Так, например, имея N деталей, мы получаем N! перестановок, а если детали могут быть ориентированы двумя способами, число перестановок будет равна (2N)!, т. е. применяется каждая из них с поворотом на 90 ° предметами. Однако, если все N деталей одного типоразмера, то результат укладки всех перестановок, очевидно, будут одинаковым, то есть число действительно различных перестановок равно 1. В общем случае количество перестановок для нахождения точного решения поставленной задачи без учета повторяющихся за счет одинаковой типоразмерности деталей будет (n₁ + n₂ + … + n_k)! / (n₁! + n₁! + … + n₁! ), что является оценкой поля для поиска решения.

На данный момент для решения задач дискретной оптимизации наиболее активно используются генетические алгоритмы. Также широкое распространение получили метаэвристики «Поиск с запретами», «Имитация отжига» и «Муравьиной колонии». Помимо выбранной методики и особенностей ее реализации конкретным автором, большое влияние на качество и быстроту получения результата оказывает выбор процедуры декодера. Под декодером обычно понимается процедура, которая позволяет на основе абстрактной информации (например, приоритетный список предметов), однозначно определить взаимное положение предметов и построить карту раскроя. Выбор декодера является важным вопросом при проектировании нового метода.

Следует отметить, что для оптимизации нахождения оптимумов размещения можно применить известные методы, такие как: муравьиные алгоритмы, генетические алгоритмы. Очевидно, что методы, использующие алгоритмы нейронных сетей, нам не подходят, так как они ориентированы на обучение с «учителем», а количество обучающих наборов в этом случае будет бесконечно велико.

На мой взгляд, наиболее подходящим методом для решения поставленной задачи будет определенным образом модифицированный генетический алгоритм, который имеет свойство сходимости в экстремумах функций. Так как поставленная задача является многоэкстремальной, можно говорить о том, что найденный экстремум не обязательно будет являться глобальным, поэтому полученный результат может отличаться от точного, но при увеличении времени обработки и предотвращении преждевременной сходимости можно получить оптимальное решение достаточное для решения задачи оптимизации производства.

Идея эволюционного алгоритма «подсмотрена» у природы и основана на четырех взаимосвязанных естественных процессах, обеспечивающих приспосабливаемость популяции к воздействию среды, а именно селекция, скрещивание, мутация и отбор. Описание программных реализаций эволюционных алгоритмов реализующих эти этапы описаны достаточно подробно в литературе и выходит за рамки данной статьи.

Хромосома, представляющая потенциальное решение может иметь соседское, порядковое или путевое представление (предварительно все детали нумеруются без учета типоразмера). Наиболее перспективной для данной задачи, по моему мнению, является путевое представление хромосомы как наиболее естественное и удобное для трансформации самого алгоритма. В работе будет предпринята попытка обработки генетического алгоритма с хромосомой аллелью, которой является номер типоразмера детали, а длина хромосомы равна количеству деталей.

Важной составляющей алгоритма является физическое размещение деталей на поверхности материала. Т.е. необходимо получить однозначную интерпретацию хромосомы как объекта возможного решения не подверженного коллизиям толкования. Для такой цели могут подойти некоторые известные эвристики такие как «первая подходящая», «лучшая» корзины (рис. 2). «Первая подходящая» эвристика размещает i-ю деталь, представленную в хромосоме в ближайшую j-ю корзину, размеры которой не меньше размера детали. «Лучшая» эвристика ищет корзину с минимальным остатком материала после размещения в ней детали. Выбор эвристики не является очевидным, так как при всей привлекательности «лучшей корзины» существуют опасения преждевременной сходимости алгоритма в локальном экстремуме. По этой причине не предполагается использование «жадного» алгоритма.

Рисунок 2 – Использование эвристик «первая подходящая корзина» и «лучшая корзина»

Выводы

В настоящее время все более актуальными становятся вопросы автоматизации производства в полном объеме с целью возможного перехода к созданию на предприятии единой информационной среды, позволяющей гибкое интегрирование современных средств проектирования, производства, управления и т.д., которые позволяют эффективно решать задачи оперативного планирования производства. Поэтому в таких условиях особенно важным становится поиск новых подходов, обеспечивающий целесообразную перестройку системы оптимального расчета карт кроя с учетом жизненных реалий. Уровень развития вычислительной техники позволяет вполне успешно решать поставленные задачи в необходимом для практики объеме и качестве. Один из таких примеров представлен в данной статье.

Дальнейшие исследования направлены на следующие этапы:

1. Проектирование и реализация программного комплекса для визуализации и вычисления эффективности расчётов.
2. Оценка существующих методов для реализации алгоритма раскроя.
3. Обоснование выбранного критерия эффективности алгоритма.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2020 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

1. Stoyan Y., Gil N., Scheithauer G. Packing of convex polytopes into a parallelepiped // Preprint.-Dresden.- MATH-NM-06-2004.-2004 - 32C.
2. Sykora A.M. Nesting problems: exact and heuristic algorithms. / A.M. Sykora// A Thesis for the degree of Doctor of Philosophy in the University of Valencia. 2010. Valence / – 187 c.
3. Lamousin H., Waggenspack W. Nesting of two-dimensional irregular parts using a shape reasoning heuristic // Computer-Aided Design. 1997. Vol. 29, N. 3.
4. Milenkovic V.J., Daniels K. Translational polygon containment and minimal enclosure using mathematical programming.-ITOR special issue with papers from IFORS'96, 1996, 30p.
5. Dykhoff, H. A typology of cutting and packing problems / H. Dykhoff //Evropean Journal of Operational research. – 1990. – Vol. 44. – P. 145-159.
6. Месягутов, М. А. Задача двухмерной ортогональной упаковки: поиск нижней границы на базе решения одномерной продолженной упаковки / М. А. Мясогутов // Информационные технологии. – М., 2010. – №6. – С. 13 – 23.
7. Основные методы решения задачи фигурной нерегулярной укладки плоских деталей [Електронний ресурс] / Р. Т. Мурзакаев, В. С. Шилов, А. В. Буркова // Электронный научный журнал : Инженерный вестник Дона. – 2013. // [Электронный ресурс]. — Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2013/2043
8. Шатат Ахмед Фуад Задача рулонного раскроя / М. А. Мясогутов // Информационные технологии. – М., 2005. // [Электронный ресурс]. — Режим доступа: http://masters.donntu.ru/2005/kita/shatat/
9. Мухачева A.C., Чиглинцев A.B. Генетический алгоритм поиска минимума в задачах двумерного гильотинного раскроя // Информационные технологии. 2001 №3. С. 27-32.
10. Норенков И.П. Эвристики и их комбинации в генетических методах дискретной оптимизации. // Информационные технологии. 1999. №1. С. 2-7.