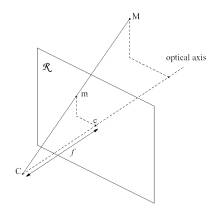
Рисунок 1 – Модель перспективной проекции
Автор: Антон Конушин
Источник: Конушин А. Геометрические свойства нескольких изображений //Компьютерная графика и мультимедиа. Вып. – 2006. – №. 4. – С. 3.
Для детального описания методов отслеживания точечных особенностей, калибровки камеры и реконструкции трехмерных объектов необходимо ввести модель перспективной проектирования и описать геометрические свойства этого преобразования. Точки нескольких изображений, полученных с помощью перспективной проекции, находятся в особых отношениях друг с другом, которые описываются эпиполярной геометрией. Модели этих отношений должны быть подробно рассмотрены, т.к. практически все методы трехмерной реконструкции требуют оценки соответствующих моделей и опираются на их свойства.
Необходимо отметить отдельно предположение, что на всех исходных изображениях запечатлена одна и та же сцена, т.е. каждое изображение является видом сцены с какой-то определенной камеры. Поэтому для удобства описания вводится понятие вида, как изображение с ассоциированной с ним моделью камеры, с которой оно было получено.
Модель перспективной проекции соответствует идеальной камере-обскуре. Эта модель довольно точно соответствует процессу построения изображения в большинстве современных фото- и видеокамер. Однако из-за ограничений современной оптики реальный процесс несколько отличается от модели камеры-обскуры. Отличия реального процесса от модели называются искажениями и моделируются отдельно.
Модель простейшей камеры-обскуры удобна тем, что она полностью описывается центром проекции и положением плоскости изображения. Поэтому проекция любой точки сцены на изображении может быть найдена как пересечение луча, соединяющего центр проекции и точку сцены, с плоскостью изображения.

Рисунок 1 – Модель перспективной проекции
Рассмотрим простейший случай, когда центр проекции камеры (фокус) помещен в начало системы координат, и плоскость изображения совпадает с плоскостью Z=1. Пусть (X,Y,Z) - координаты точки в 3-х мерном пространстве, а (x,y) - проекция этой точки на изображение I. Перспективная проекция в этом случае описывается следующими уравнениями:
 (2.1)
(2.1)В матричной форме с использованием однородных координат эти уравнения переписываются в следующем виде:
 (2.2)
(2.2)Плоскость, расположенная на расстоянии 1 от центра проекции, и перпендикулярная оптической оси называется идеальной плоскостью изображения. Оптическая ось пересекает идеальную плоскость изображения в точке с, называемой принципиальной точкой. Иллюстрация простейшего случая перспективной проекции приведена на рис. 1.
Простейший случай перспективной проекции практически всегда не соответствует реальной камере. Расстояние от центра проекции до плоскости изображения, т.е. фокусное расстояние, обозначаемое f, обычно не равно 1. Также координаты точки в плоскости изображения могут не совпадать с абсолютными координатами. При использовании цифровой камеры, соотношение между координатами точки в изображении и абсолютными координатами точки на идеальной плоскости, определяется формой и размерами пикселов матрицы.
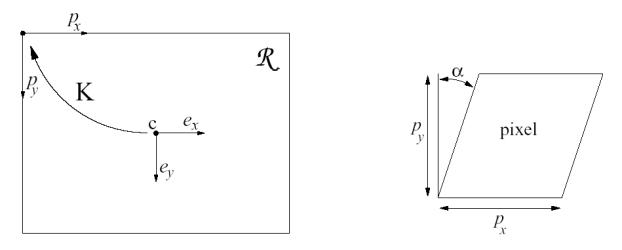
Рисунок 2 – Преобразование из координат идеальной плоскости в координаты изображения
Обозначим размеры пиксела матрицы цифровой камеры за px, py, угол наклона пиксела за α, а принципиальную точку за [cx, cy,1], рис.2. Тогда координаты точки (x,y) в изображении, соответствующей точке (xR, yR) на идеальной плоскости, определяются выражением:
 (2.3)
(2.3)Если за fx,fy обозначить фокусное расстояние f, измеренное в ширинах и высотах пикселей, а tan(α)*f/py обозначить как s, то формула 2.3 преобразуется в:
 (2.4)
(2.4)Матрица K называется матрицей внутренней калибровки камеры. В большинстве случаев у реальных цифровых камер угол наклона пикселей близок к прямому, т.е. параметр s=0, а ширина и высота пикселя равны. Принципиальная точка обычно располагается в центре изображения. Поэтому матрица K может быть записана в виде:
 (2.5)
(2.5)Это предположение о виде матрицы K широко используются для упрощения алгоритмов определения внутренней калибровки камеры, а также при синтетическом моделировании изображений, необходимых для оценки качества и эффективности методов трехмерной реконструкции.
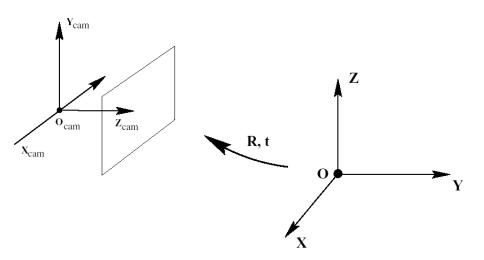
Рисунок 3 – Евклидово преобразование пространства из системы координат сцены в систему координат, связанную с камерой
Пусть M - точка сцены в 3-х мерном пространстве. Любое движение является евклидовым преобразованием пространства, поэтому в однородных координатах оно выражается как:
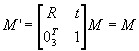 (2.6)
(2.6)где R - матрица вращения, T=[t1,t2,t3]T - вектор переноса.
Движение камеры относительно сцены эквивалентно обратному движению точек сцены относительно камеры, поэтому равно:
 (2.7)
(2.7)где R, T - матрица вращения и вектор перемещения камеры относительно сцены. Матрица С называется матрицей внешней калибровки камеры. Матрица C-1 называется матрицей движения камеры. Таким образом, матрица внешней калибровки камеры переводит координаты точек сцены из системы координат сцены в систему координат, связанную с камерой.
Из выражений 2.1, 2.4, 2.7 можно вывести выражение произвольной перспективной проекции для любой камеры с произвольной ориентацией и положением в пространстве:

В более краткой форме с учетом предыдущих обозначений эта формула может быть записана как:

Матрица P называется матрицей проекции камеры.
По аналогии с общим перспективным преобразованием рассмотрим вначале простейший случай перспективного преобразования плоскости. Пусть плоскость p совпадает с плоскостью Z=0, тогда однородные трехмерные координаты любой ее точки M=[X,Y,0,1]. Для любой камеры с матрицей проекции P, перспективное преобразование плоскости описывается матрицей размерности 3*3:
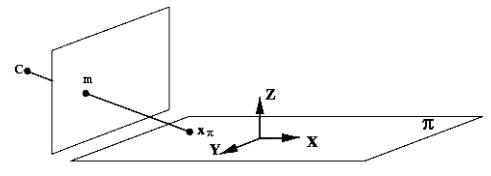

Рисунок 4 – Перспективное преобразование плоскости
Поскольку любую плоскость в 3-х мерном пространстве можно перевести в плоскость Z = 0 евклидовым преобразованием поворота и переноса, что эквивалентно домножению матрицы камеры P на матрицу преобразования L, то перспективное отображение произвольной плоскости в пространстве описывается линейным преобразованием с матрицей размерности 3*3.
Перспективное преобразование плоскости также называется гомографией. В матричной форме перспективное преобразование плоскости записывается как m=HM.
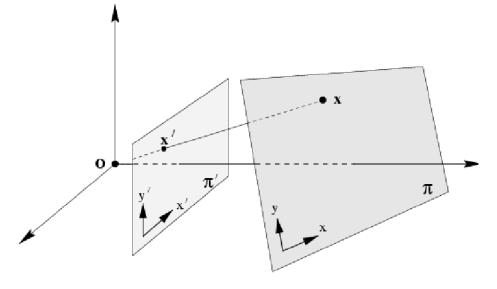
Рисунок 5 – Перспективное преобразование произвольной плоскости в 3-х мерном пространстве
Запечатленная на всех исходных изображениях сцена считается неподвижной, поэтому взаимное расположение проекций точек сцены на разных кадрах не может меняться произвольным образом. Ограничения, накладываемые на расположение проекций точек, очевидно зависят от параметров камер и их положения друг относительно друга. Поэтому определение моделей таких ограничений дает часть информации о взаимном расположении камер, с которых были получены изображения.
Если центры двух камер совпадают, то точки на плоскостях изображения обеих камер переводятся друг в друга перспективным преобразованием плоскости. В этом случае, преобразование точек между изображениями не зависит от формы 3-х мерной сцены, а зависит только от взаимного положения плоскостей изображений.
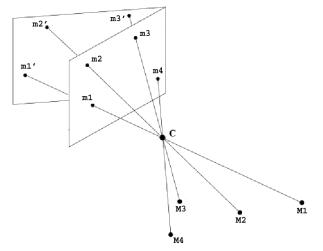
Рисунок 6 – Перспективное преобразование плоскости между плоскостями изображений двух видов с совпадающими центрами камер
Если вся сцена или ее часть представляет собой плоскость, то ее изображения на разных видах с несовпадающими центрами камер, можно перевести друг в друга преобразованием гомографии. Пусть p - наблюдаемая плоскость, H1 - преобразование гомографии между плоскостью p и изображением I1, H2- преобразование гомографии между плоскостью p и изображением I2. Тогда преобразование гомографии H12 между изображениями I1 и I2 можно вывести следующим образом:

H12 не зависит от параметризации плоскости p, а значит не зависит и от системы координаты в пространстве
Большинство методов определения координат 3х мерных точек по их проекциям и методов реконструкции 3-х мерной сцены, опираются на предположение о движении центра камеры между видами. Поэтому при совпадении центров камер нескольких видов эти методы будут давать некорректные результаты. Такие конфигурации камер должны обнаруживаться и обрабатываться специальным образом.
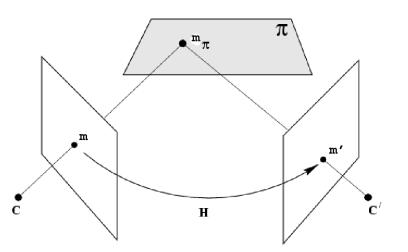
Рисунок 7 – Перспективное преобразование плоскости между точками двух изображений с разными центрами камер, если наблюдаемая сцена является плоскостью
Поскольку преобразование гомографии записано в однородных координатах, то матрица H определена с точностью до масштаба. Она имеет 8 степеней свободы, и параметризируется 8 переменными. Каждое известная пара соответствующих точек m1 и m2 на первом и втором изображении соответственно дает 2 линейных уравнения от элементов матрицы H. Поэтому 4-х известных пар соответствующих точек достаточно для составления системы линейных уравнений из 8 уравнений с 8 неизвестными. По этой системе гомография H может быть однозначно определена, если никакие три из точек не лежат на одной прямой.
Рассмотрим случай, когда центры камер двух видов не совпадают. Пусть C1 и C2- центры двух камер, M - 3-х мерная точка сцены, m1 и m2 - проекции точки M на первое и второе изображение соответственно. Пусть П - плоскость, проходящая через точку M и центры камер C1 и C2. Плоскость П пересекает плоскости изображений первого и второго видан по прямым l1 и l2. Поскольку лучи C1M и C2M лежат в плоскости П, то очевидно, что точки m1 и m2 лежат на прямых l1 и l2 соответственно. Можно дать более общее утверждение, что проекции любой точки M', лежащей в плоскости П, на оба изображения должны лежать на прямых l1 и l2. Эти прямые называются эпиполярными линиями. Плоскость П называются эпиполярной плоскостью.
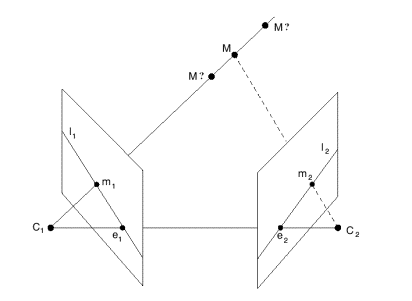
Рисунок 8 – Эпиполярная геометрия двух видов
Два вида одной и той же сцены называются стереопарой, а отрезок C1C2, соединяющий центры камер, называется базой стереопары (baseline) или стереобазой. Любая эпиполярная плоскость проходит через отрезок C1C2. Пусть C1C2 пересекает первое и второе изображение в точках e1 и e2 соответственно. Точки e1 и e2 называются эпиполярными точками или эпиполями. Все эпиполярные линии пересекаются в точках e1 и e2 на первом и втором изображении соответственно. Множество эпиполярных плоскостей представляет собой пучок, пересекающийся по стереобазе C1C2. Множество эпиполярных линий на обоих изображений также представляют собой пучки прямых, пересекающихся в e1 и e2 .
Точки m1 и m2 называются соответствующими, если они являются проекциями одной и той же точки сцены M. Эпиполярные линии l1 и l2 называются соответствующими, если они лежат в одной и той же эпиполярной плоскости П. Если эпиполярная плоскость П проходит через точку m1, тогда эпиполярные линии l1 и l2, лежащие в ней, называются соответствующими точке m1.
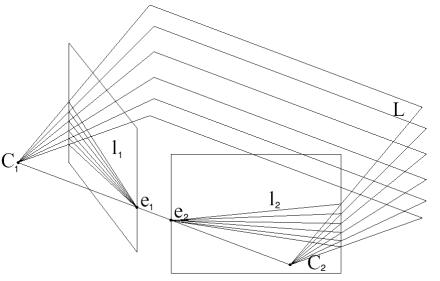
Рисунок 9 – Пучок эпиполярных плоскостей
Ограничение на положение соответствующих точек m1 и m2, вытекающей из эпиполярной геометрии, можно сформулировать следующим образом: точка m2, соответствующая m1, должна лежать на эпиполярной линии l2, соответствующей m1 . Это условие называется эпиполярным ограничением. В однородных координатах условие того, что точка m лежит на линии l записывается как lTm=0 . Эпиполярная линия проходит также через эпиполярную точку. Уравнение прямой, проходящей через точки m1 и e1 можно записать как:
где [e1]x - антисимметричная матрица размерности 3*3 такая что, [e1]xm1 - векторное произведение m1 и e1.
Для соответствующих эпиполярные линий l1 и l2 верно:

где P+ - псевдоинверсия матрицы P.
Матрица F называется фундаментальной матрицей. Она представляет собой линейный оператор, сопоставляющей каждой точке m1 соответствующую ей эпиполярную линию l2. Для каждой пары соответствующих точек m1 и m2 верно
Это формулировка эпиполярного ограничения через фундаментальную матрицу.
Фундаментальная матрица имеет 7 степеней свободы. Каждая пара соответствующих точек m1 и m2 задает одно линейное уравнение на элементы матрицы, поэтому она может быть вычислена по известным 7 парам соответствующих точек.
Эпиполярное ограничение справедливо для любых пар соответствующих точек, расположенных на идеальных плоскостях двух видов. Если известны матрицы внутренней калибровки K1 и K2 камер обоих видов, то эпиполярное ограничение для соответствующих точек на идеальных плоскостях записывается как:

Матрица E называется существенной матрицей. Можно показать, что существенная матрица также может быть получена из взаимного расположения камер.
Пусть P1=(I|0) и P2=(R|-RT) - две матрицы проектирования с калибровкой K = I. Тогда уравнения проектирования на идеальную плоскость обеих камер записываются в виде:

Найдем эпиполярную линию на втором виде, соответствующую точке m'1 на первом. Для этого достаточно спроектировать на второй вид две точки, лежащие на луче (C1,m'1) на второй вид, например центр первой камеры (0,0,0,1)T и точку на плоскости бесконечности (x'1,y'1,z'1,0)T. Проекциями этих точек будут являться соответственно -RT, и R(x'1,y'1,z'1,0)T. Уравнение эпиполярной линии l2 , проходящей через обе этих точки задается как векторное произведение:
В матричной форме векторне произведение T×(x'1,y'1,z'1)T можно записать с помощью матрицы S:

Тогда эпиполярное ограничение на точки в идеальной плоскости записывается как:

Выражение существенной матрицы через параметры внешней калибровки двух камер используется для вычисления относительного положения камер.
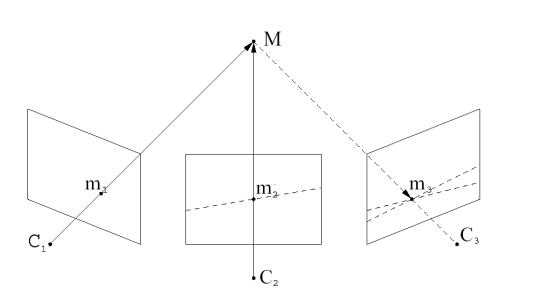
Рисунок 10 – Определение положение проекции точки М на на третьем виде по двум эпиполярным ограничениям между первым и вторым и третьем виде
Пусть C1,C2 и C3 - центры трех видов одной и той же трехмерной сцены. В этом случае, эпиполярные ограничения накладываются на соответствующие точки любой пары видов. Если известны проекции двух точек m1 и m2 на первый и второй вид, то положение проекции на третье изображение может быть найдено как пересечение двух эпиполярных видов, соответствующих точкам m1 и m2.
По двум известным проекциям m1 и m2 на два изображения с известной калибровкой можно определить положение точки M в пространстве. Поэтому если известна калибровка третьего изображения, то проекция точки M на третий вид может быть определена простой проекцией.
Ограничения, накладываемые на положение соответствующих точек более двух изображений, также можно записать в линейной форме. Для трех видов эти ограничения записываются в виде трифокального тензора, для четырех видов - в форме квадрифокального тензора. Однако вычисление этих ограничений эквивалентно вычислению калибровки всех трех или четырех видов в проективном пространстве. В этой работе эти виды ограничений не используются, поэтому более подробно не рассматриваются.