Реферат по теме выпускной работы
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2021 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Содержание
- Введение
- 1.Методы геометрического моделирования
- 2.Комплекс универсальных аналитических методов моделирования сложных геометрических объектов и их преобразований
- 2.1 Метод гладкого сопряжения кривых и плоскостей
- 2.2 Метод поворота геометрического объекта вокруг оси, проходящей через заданную точку пространства
- Заключение
- Список источников
Введение
Математическое моделирование физико–механических процессов и инженерных сооружений часто связано с необходимостью создания геометрических моделей. С их помощью можно определить образ существующего или проектируемого объекта, провести соответствующий постановке задачи численный эксперимент и осуществить необходимые коррекции. Геометрической моделью в широком смысле называется совокупность формального описания исследуемого объекта и соответствующего ему визуального образа, представленного в пространствах различной размерности. Формальным описанием в связи с развитием современных методов компьютерного моделирования в первую очередь является численное моделирование геометрических объектов окружающего мира. При этом их многообразие создается с использованием базовых геометрических элементов: точки, линии и поверхности.
1.Методы геометрического моделирования
Геометрическое моделирование в настоящее время развивается по двум направлениям. Первое направление – численные методы в задачах САПР и компьютерной графики. Современные этапы внедрения САПР характеризуются переходом от плоского моделирования к объемному. Точность модели геометрического объекта обеспечивается точностью осуществления преобразования базового примитива. Для плоского моделирования, основными объектами моделирования являются отрезки, дуги, полилинии и кривые, в том числе кривые Безье, сплайны, рациональные кривые. Базовые преобразования на их основе – продление, обрезка и соединение. В объемном моделировании основные объекты – это замкнутые контуры. При этом используются поверхности движения, линейчатые, поверхности Безье, Кунса. Главные операции – булевы: объединение, дополнение, пересечение, а также преобразования поворота и трансляции. Существует понятие базовой поверхности, с которой в процессе моделирования осуществляют то или иное преобразование. В результате средствами САПР проектируемый объект численно конструируется из геометрических тел, называемых графическими примитивами, которые могут быть трансформированы теми или иными программными средствами. Аналитического представления новых форм, получаемых такими преобразованиями, не существует.
Второе направление геометрического моделирования представлено работами, где геометрические объекты задаются в аналитическом виде. Выделено более 500 аналитически заданных поверхностей 38 классов, которые могут быть использованы при решении различных задач науки и техники. Аналитические методы представления геометрических объектов обладают высокой степенью точности. Возможны различные формы описания объектов и их преобразований – векторные, операторные, тензорные и иные формы, что позволяет задавать каждую точку геометрического объекта и выполнять произвольные преобразования в аналитическом виде. В основе классификации аналитических поверхностей существенную роль имеют те способы, в результате которых эти поверхности получаются. Существует большой класс поверхностей, которые получены преобразованием вращения плоской кривой вокруг оси Oz. Еще один обширный класс поверхностей получается преобразованием переноса кривой некоторого направления, так что ее одна точка скользит по другой кривой. Более сложные преобразования образуют классы винтовых, спиралевидных и других поверхностей. Пополнение известного набора аналитических поверхностей новыми и расширение их классов представляет интерес для развития методов геометрического моделирования и их приложений. Важной составляющей исследований в этом направлении может быть расширение многообразия поверхностей и создание новых аналитических форм путем различных преобразований: дополнений, поворотов, пересечений и других. Использование аналитических методов может являться начальным этапом проектирования. Это позволяет после верификации соответствующих геометрических моделей транслировать их в графические пакеты, поддерживающие геометрические масштабы для получения проектной документации.
Существуют алгоритмы гладкого сопряжения кривых и плоскостей при разработке системы геометрического моделирования машиностроительных деталей на основе численных методов. Для их применения требуется описать объекты сопряжения в форме поверхности или кривой Безье, или сплайновой поверхности соответственно, как рассмотрено в работах. Степень гладкости сопряжения зависит от числа контрольных точек, что в свою очередь увеличивает алгебраическую степень кривых, и затрудняет численные расчеты. Более широко данные методы моделирования используются для поверхностного моделирования сложных объемных форм.
Сопряжение поверхностей в компьютерной геометрии осуществляется для операции скругления ребер. Для этого строят новые грани, которые различным образом сопрягают тела, которые стыкуются в скругляемых ребрах. В основе этих методов лежат геометрические алгоритмы с использованием поверхностей скругления постоянного радиуса и поверхностей, представляющие собой следы от качения сферы, частей цилиндрических поверхностей и поверхностей тора. В случае если требуется построить поверхность переменного радиуса, то опорная дуга поверхности сопряжения представляется в виде рациональной кривой Безье. Также рассматриваются и гладкие сопрягаемые поверхности – эллиптические, параболические и гиперболические, которые получаются варьированием функции веса средней точки, заданной рациональной кривой Безье. При этом не исследовался вопрос кривизны и степени гладкости такого сопряжения. Возникающая от привлечения численных методов погрешность, в описанных методах гладкого сопряжения при определении точек касания требует дополнительных исследований.
Исследованию преобразования центрального проецирования посвящен раздел геометрии – проективная геометрия, которая развилась и выделилась в отдельную ветвь знаний в первые десятилетия 19 века в связи с потребностью развития теории изображений в перспективе. Геометр Жан Виктор Понселе один из первых выделил особые свойства геометрических фигур, названные им проективными. Проективная геометрия составляет геометрию класса проективных преобразований и представляет из себя систему теорем, утверждающих низменность свойств фигур в этом классе. Идея классификации различных отраслей геометрии в соответствии с классами преобразований принадлежит Феликсу Клейну.
Метод создания перспективного изображения широко применяется в компьютерной графике при создании реалистического изображения. В основе метода в популярных и конкурирующих между собой пакетах OpenGL и DirectX лежит построение так называемой проекционной матрицы и ее применение для создания проективного изображения. Преобразование осуществляется с использованием однородных координат с переходом на заключительной стадии к декартовым для определения положения координаты трёхмерной вершины на двумерном экране монитора.
Формирование проекционной матрицы для создания требуемой иллюзии осуществляется с помощью четырёх параметров: угол обзора в радианах – fovy, соотношение сторон – aspect, расстояние до ближней плоскости отсечения (n), расстояние до дальней плоскости отсечения – f.
В данных методах объект проецирования задается организованным программным образом массивом координат. При использовании аналитических форм возникает обязательная необходимость в переходе к таким массивам перед осуществлением преобразования проецирования. Используются различные методы, в частности, триангуляции, для возможности выполнения процедур в соответствии с аксиоматикой проективной геометрии. Серьезные вычислительные трудности возникают в тех случаях, когда проецируемый объект, плоскость проецирования или центр проецирования меняют свое положение в пространстве произвольным образом. Все алгоритмы получения проективных изображений связаны с необходимостью переходов от декартовых координат к однородным и затем требуют выполнение обратного перехода.
2.Комплекс универсальных аналитических методов моделирования сложных геометрических объектов и их преобразований
При этом для задания геометрических объектов и их преобразований используется векторное представление, не зависимое от выбранного координатного базиса, на всей стадии решения. Такое представление можно назвать инвариантным. Понятие инвариантности базируется на концепции Ф.Клейна, как свойстве некоторого класса математических объектов, остающихся неизменными при преобразованиях, и на принципе инвариантности геометрических понятий Г.Ф.Лаптева, как связи геометрических понятий с рассматриваемой фигурой, полностью определяемые фигурой и не зависящие от способа ее задания. Формальным инструментом для построения математических моделей являются векторы и кватернионы, как объекты, позволяющие осуществлять алгебраические преобразования, сохраняя принцип инвариантности геометрических понятий. Основными компонентами решения являются алгебраический подход к решению векторных уравнений, включая дифференциальные и аналитический метод построения кривых и поверхностей.
2.1 Метод гладкого сопряжения кривых и плоскостей
Многообразие форм аналитических поверхностей позволяет решать различные задачи геометрического моделирования в графическом дизайне, архитектурно–строительной сфере, судо– и авиастроении, машиностроении. Расширению возможности аналитических методов задания поверхностей в задачах формообразования может способствовать гладкое сопряжение плоскостей. Гладкое сопряжение с использованием примитивов в качестве инструмента сглаживания или скругления постоянного/переменного радиуса эффективно применяется в CAD–системах.
Рассмотрим аналитический метод гладкого сопряжения плоскостей на примере сопряжения двух пересекающихся плоскостей, произвольно ориентированных в пространстве, что позволяет получить поверхность сопряжения в аналитическом виде с заданным порядком гладкости.
На первом этапе решения задачи введем в рассмотрение две плоскости S1 и S2, которые заданы своими нормальными единичными векторами и радиус–векторами r1,r2 фиксированных точек (рис.2.1).
Аналитическая запись линии пересечения плоскостей может быть представлена системой векторных уравнений
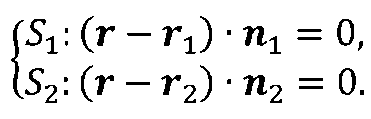
(рис 2.1)
Первый шаг процедуры решения поставленной задачи заключается в получении линии пересечения плоскостей в параметрической форме
Уравнение линии пересечения плоскостей L ищется в следующей параметрической форме
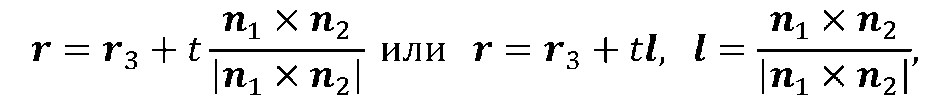
(рис 2.2)где r3 – радиус–вектор точки на прямой L, l – единичный вектор этой прямой.
На следующем шаге находится положение такой точки М3, которая лежит на пересечении прямой L с перпендикулярно расположенной к ней прямой, лежащей в плоскости St и проходящей через точку Мг. Положение этой точки может быть найдено путем решения системы следующих уравнений
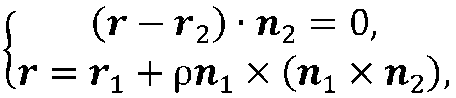
(рис 2.3)где р – параметр системы.
Первое уравнение задает плоскость S2, а второе уравнение задает прямую в параметрической форме, проходящую через точку М1; лежащую в плоскости S1 и перпендикулярную L.
Подставим в систему (2.3) радиус–вектор точки М3 . Исключая из этой системы вектор г3, находим значение параметра р
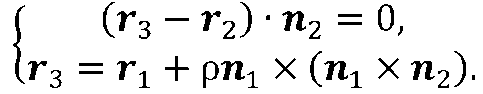
Исключая из этой системы вектор r3, находим значение параметра р
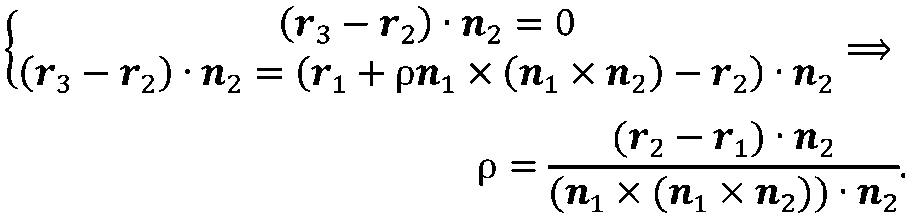
Подставляя найденное значение параметра р во второе равенство системы (2.3), находим положение точки М3
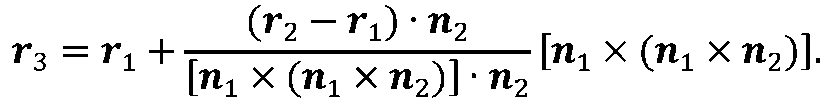
(рис 2.4)
С использованием тождества
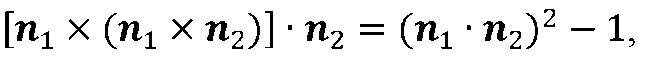
Которое вытекает из правила вычисления двойного векторного произведения, формула (2.4) преобразуется к виду
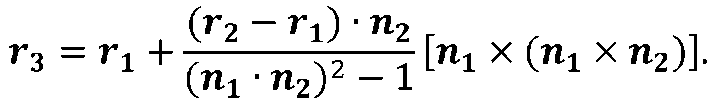
Подстановка полученного значения г3 в формулу (2.2) дает уравнение линии пересечения плоскостей St и S2 в инвариантной параметрической форме
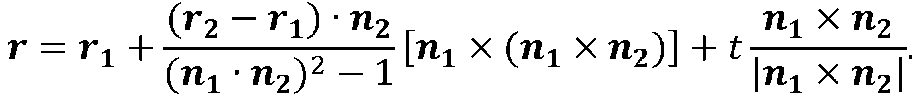
(рис 2.5)
При этом знаменатель обращается в ноль, когда плоскости параллельны.
Дальнейшее решение задачи гладкого сопряжения плоскостей заключается в нахождении лучей L1и L2. Лучи Lt и L2 исходят из точки М3, лежат в плоскостях S1 и S2 и перпендикулярны к прямой L.
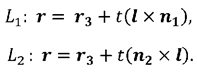
Далее на лучах Lt и L2 выбираются точки на расстояниях dt и d2 от линии пересечения плоскостей. Их положение при этом определяется равенствами
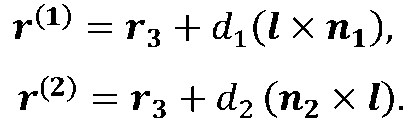
Гладкое сопряжение лучей Lt и L2 осуществляется с помощью векторного полинома пятой степени
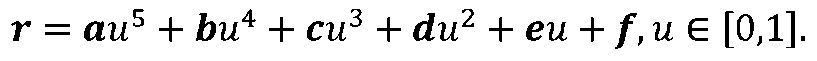
(рис 2.6)
Степень полинома выбирается из условий обеспечения гладкого сопряжения лучей L1 и L2, при котором выполняются следующие краевые условия:
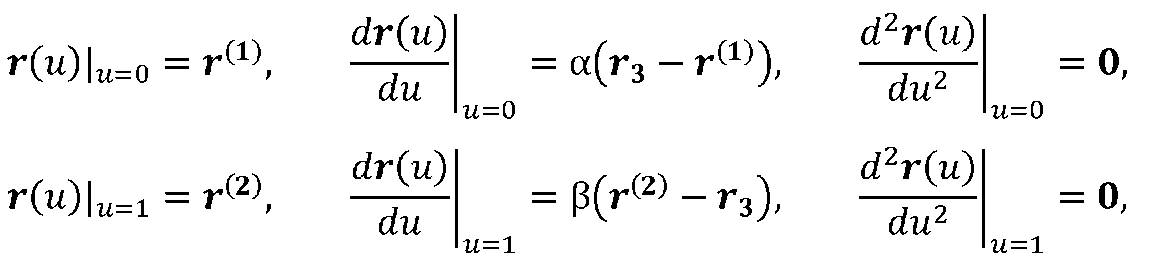
Подстановка векторного полинома (2.6) в краевые условия приводит к следующей системе линейных уравнений с векторными неизвестными
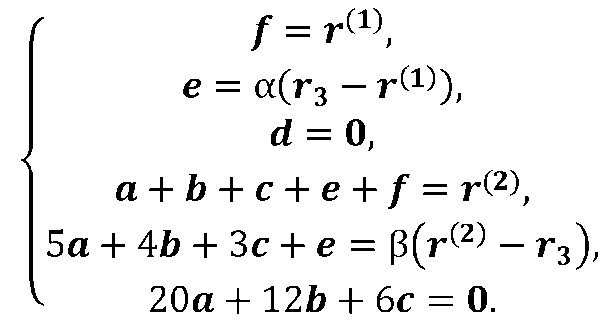
Эта система сводится к матричному уравнению относительно трёх неизвестных векторов а, b, с.
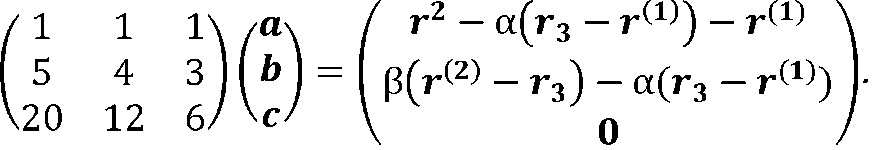
Решение этой системы в инвариантной форме записывается равенством
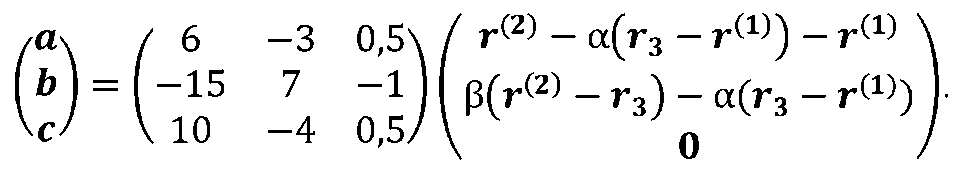
Откуда
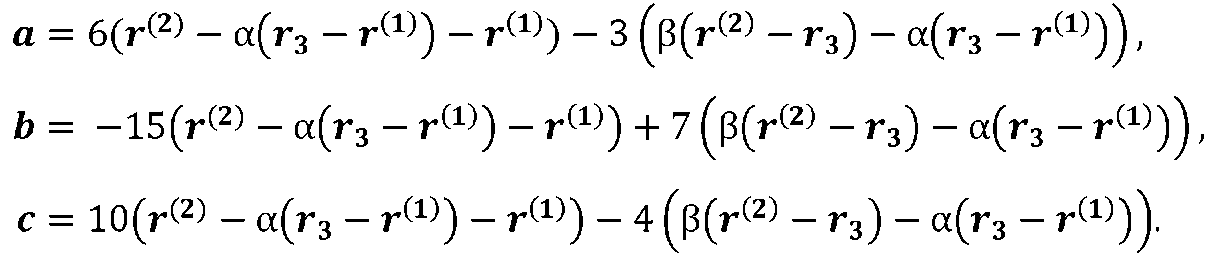
Окончательно, поверхность, реализующая гладкое сопряжение плоскостей S1 и S2, находится, как поверхность переноса с образующей в виде полинома пятой степени (2.6) и направляющим вектором l.
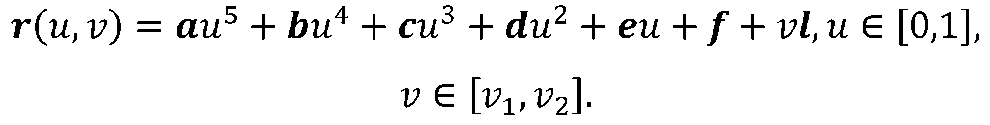
(рис 2.7)
В качестве примера рассматривается сопряжение, выполненное в системе компьютерной алгебры Mathcad, двух плоскостей (рис.2.2).
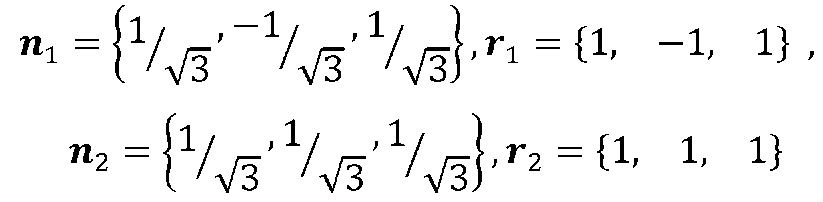
при значениях параметров
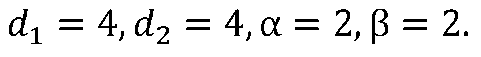
По уравнению образующей кривой
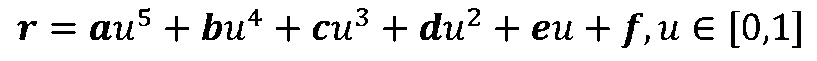
определяется кривизна на интервале сопряжения по формуле
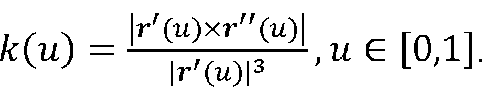
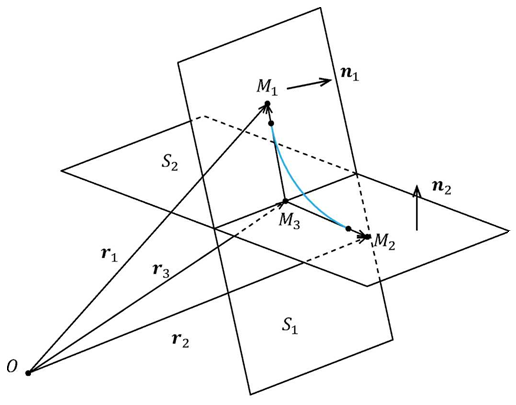
Базовая линия сопряжения двух плоскостей
2.2 Метод гладкого сопряжения кривых и плоскостей
Поворот или вращение трехмерного евклидова пространства вместе с параллельным переносом образуют так называемую подгруппу движения группы аффинных преобразований. Математические алгоритмы преобразования поворота востребованы при решении различных задач динамики твердого тела, робототехники, мультипликации, твердотельного моделирования. Для решения задач используются различные алгоритмы. Так, поворот вокруг оси произвольным образом ориентированной в пространстве традиционно решается путем последовательного выполнения операций параллельного переноса и поворота вокруг координатных осей.
Рассмотрим обобщенный метод поворота вокруг оси с единичным направляющим вектором I, проходящей через заданную точку пространства Мг. При таком преобразовании все точки оси остаются неподвижными, а остальные точки поворачиваются в плоскостях перпендикулярных этой оси на один и тот же угол д .
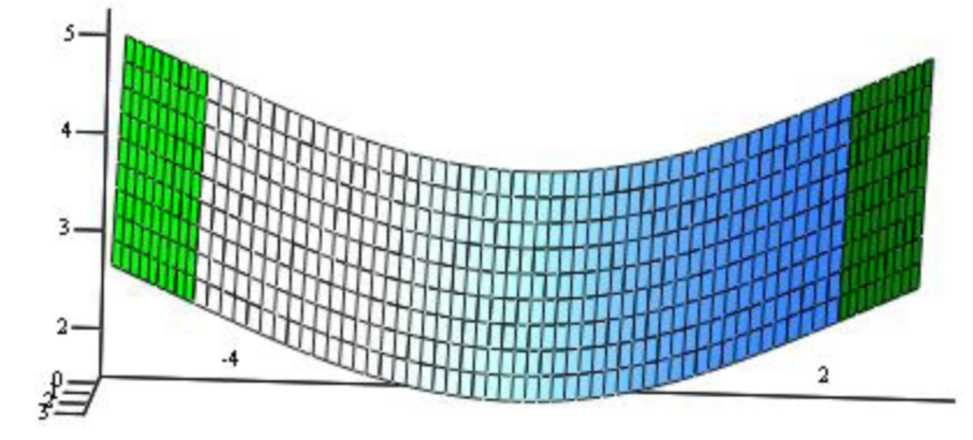
Поверхность гладкого сопряжения двух плоскостей
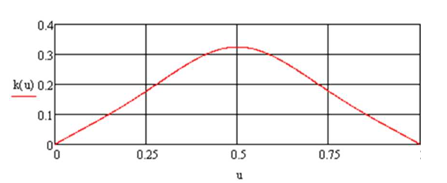
График изменения кривизны образующей кривой поверхности гладкого сопряжения, построенный в системе компьютерной алгебры Mathcad
С учетом равенства
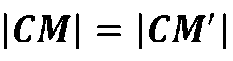
имеем
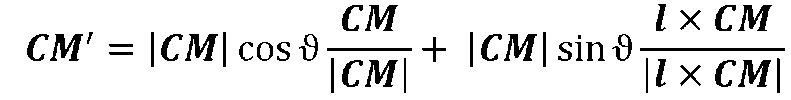
или
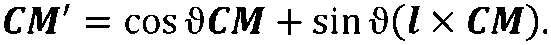
Из геометрических соображений находим, что
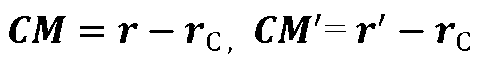
При этом
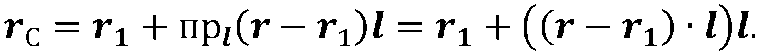
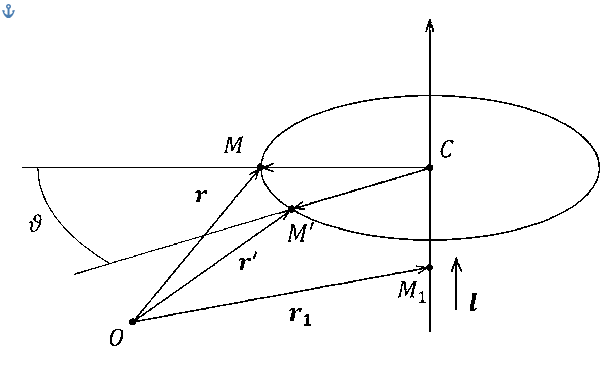
Схема поворота точки М евклидова пространства вокруг произвольной оси, с единичным направляющим вектором I, проходящей черезточку Мг
Как следует из графика изменения кривизны образующей кривой (рис. 2.3) при данных значениях корректирующих параметров аир изменение кривизны образующей кривой происходит симметрично. Путем варьирования этих параметров изменение кривизны может быть реализовано по разным законам с учётом требуемых целей моделирования.
Заключение
По результатам анализа существующих методов геометрического моделирования установлено, что при математическом моделировании сложных геометрических объектов и их преобразований используются два основных подхода – численные методы в задачах САПР, компьютерной графики и аналитическое геометрическое моделирование. Средствами САПР проектируемый объект численно конструируется из геометрических тел, называемых графическими примитивами, которые могут быть трансформированы теми или иными программными средствами. Точность модели геометрического объекта обеспечивается точностью осуществления поточечного преобразования базового примитива. Аналитические же методы обладают высокой степенью точности результатов моделирования, так как аналитически задается каждая точка геометрического объекта и преобразования выполняются синхронно.
Существуют алгоритмы гладкого сопряжения кривых и плоскостей при разработке системы геометрического моделирования машиностроительных деталей методами САПР на базе использования численных методов. Степень гладкости сопряжения зависит от числа контрольных точек, что увеличивает и алгебраическую степень кривых сопряжения и затрудняет численные расчеты.
Операцию скругления ребер осуществляют методами компьютерной геометрии, в основе которых лежит сопряжение в аналитической форме с использованием поверхностей постоянного радиуса
Основным применением методов создания перспективных изображений является решение задач компьютерной визуализации. Теоретические основы соответствующих методов заложены в проективной геометрии. Основными инструментами при моделировании построения центральной проекции являются проективные матрицы в однородных координатах с использованием глобальных и локальных систем координат. Объект проецирования задается поточечно – числовым массивом его координат. Расположение плоскости проецирования является строго фронтальной.
Наряду с рассмотренными, возможен иной поход к математическому моделированию представленных выше преобразований, когда объекты моделирования заданы в аналитической форме, а все преобразования выполняются в аналитическом виде независимо от выбора системы координат.
Обзор существующих методов описания поворота твердого тела, как наиболее широко используемого преобразования, свидетельствует о большом разнообразии подходов к решению задачи. Объединяющим является использование в разных формах представления матрицы поворота вокруг оси, проходящей через начало координат. Поворот вокруг оси, проходящей через произвольную точку пространства осуществляется путем композиции преобразования поворота относительно координатных осей и преобразования трансляции. При этом обязательным условием является введение подвижной и неподвижной системы отсчета.
Эффективным средством описания сферического движения твердого тела является использование кватернионной параметризации, которая в последние годы находит все большее применение в задачах управления движением, робототехники и компьютерной анимации. При этом популярность приобретает метод сферической линейной интерполяции кватернионов. Методы нелинейной интерполяции кватернионов, позволяющих в более широком диапазоне задавать кинематические законы сферического движения в научной литературе отсутствуют. Представляется целесообразным получение независимых от выбора системы координат и удобных для реализации в пакетах компьютерной алгебры алгоритмов описания поворота твердого тела относительно оси произвольного положения.
Результат обзора позволяет сделать вывод о целесообразности создания универсальных математических методов для аналитического описания сложных геометрических объектов и их преобразований в основе которых лежит выполнение требований независимости от выбора системы координат и совместимости с существующими аналитическими представлениями объектов
Именно такие методы позволят осуществить компьютерное моделирование преобразований сложных геометрических объектов в пакетах компьютерной алгебры.
Список источников
- Казанович Я.Б. Сегментация изображений с помощью динамических нейронных сетей / Я.Б. Казанович. // Научная сессия МИФИ–2008. Х Всероссийская научно–техническая конференция
Нейроинформатика–2008
: Лекции по нейроинформатике – Часть 2. – М.: МИФИ, 2008. – C. 37–97. - Запрягаев, С.А. Программная оболочка для поиска примитивов на изображении / С.А.Запрягаев, А.И. Сорокин. // Вестник ВГУ, Серия Системный анализ и информационные технологии – №2 – 2008. – С. 37–47.
- Введение в контурный анализ: приложения к обработке изображений и сигналов / Под ред. Я.А.Фурмана. – М.: ФизматЛит, 2003. – 592 с.
- Виноградов, А.Н. Выделение и распознавание локальных объектов на аэрокосмических снимках / [Виноградов А.Н. и др.]. // Авиакосмическое приборостроение – № 9 – 2007. – С.39–45.
- Хайкин, С. Нейронные сети: полный курс / С. Хайкин., [пер. с англ.]. – 2–е изд. – М.: Вильямс, 2006. – 1104 с.
- Ермоленко, А.В. Применение преобразования Фурье для преобразования объектов при нейросетевом анализе образов / А.В. Ермоленко. // Сборник трудов конференции
Интегрированные модели и мягкие вычисления в искусственном интеллекте
– М.: Изд–во МГТУ им. Н.Э. Баумана, 2009. – C. 39–75. - Бочаров, Д.М. Методы преобразования 2D–фотографий помещения в 3D–модель / Д.М. Бочаров, Р.А. Сорокин // Сучасні інформаційні системи і технології: матеріали другої міжнародної науково–практичної конференції (Суми, 21–24 травня 2013 року.) / Сумський державний університет. – Суми, – 2013. – С. 150–151.
- Бочаров, Д.М. Предварительная обработка 2D–изображений при 3D–реконструкции / Д.М. Бочаров, Р.А. Сорокин // Искусственный интеллект. Интеллектуальные системы ИИ–2013 : материалы международной научно–технической конференции (пос. Кацивели АР Крым, 23 – 27 сентября 2013 года) / Донецкий национальный технический университет. Донецк, – 2013.– С.70–72.
- Бочаров, Д.М. Фильтрация и сегментация изображений для задач 3D–реконструкции / Д.М. Бочаров, Р.А. Сорокин // Информационные управляющие системы и компьютерный мониторинг : материалы V международной научно–технической конференции студентов, аспирантов и молодых ученых (Донецк, 22 – 23 апреля 2014 года) / Донецкий национальный технический университет. – Донецк, – 2014. – С. 398–404.
- Кудряшов, А.П. Реконструкция трехмерных сцен городской обстановки / А.П. Кудряшов // Информационные технологии. – № 7. – 2009. – С. 63–68.
- Сорокин, Р.А. Выделение геометрических фигур на фотоизображении / Р.А. Сорокин, Д.М. Бочаров // Инновационные перспективы Донбасса : материалы международной научно–практической конференции (Донецк, 20–22 мая 2015 года) / Донецкий национальный технический университет. – Донецк, – 2015. – С. 86–90.
