Реферат по теме выпускной работы
На момент написания данного реферата магистерская работа не завершена. Предполагаемая дата завершения – май 2022 г. Полный текст работы, а также материалы по теме могут быть получены у автора или его руководителя после указанной даты. .
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- 3.1 Обзор международных источников
- 3.2 Обзор национальных источников
- 4. Моделирование движения автотранспорта с помощью клеточных автоматов
- Выводы
- Список источников
Введение
В настоящее время в больших городах существует проблема перегрузки общественного транспорта в так называемые «часы пик». В эти часы нагрузка на общественный транспорт непропорционально возрастает, что приводит к тому, что он не справляется с пассажиропотоком. Это означает, что люди не могут вовремя добраться до работы или добираются в подавленном состоянии из-за перегруженности транспорта. В свою очередь, данные факторы негативно сказываются на производительности труда работников и, как следствие, на росте экономики города.
Транспортная система в наиболее общем случае – это образующая связанное целое совокупность работников, транспортных средств и оборудования, элементов транспортной инфраструктуры и инфраструктуры субъектов перевозки, включая систему управления, направленная на эффективное перемещение грузов и пассажиров.
Эффективность транспортной системы не может рассматриваться только в рамках достижения оптимальности выполнения соответствующих процессов внутри системы. Основными задачами транспортной системы являются удовлетворение потребности экономики в перевозке грузов и обеспечение мобильности населения. В связи с этим эффективность транспортной системы всегда будет определяться неким балансом между противоречивыми требованиями экономики и общества. Ярким примером является желание пассажира, чтобы транспорт подъехал к остановке, как только пассажир подошел к ней, и желание перевозчика установить такой интервал движения, чтобы транспортные средства всегда были заполнены полностью и приносили, максимальный доход. Таким образом, для построения эффективной транспортной системы необходимо познания в области транспорта сочетать с экономикой, градостроительством, географией, экологией, социологией и психологией.
1. Актуальность темы
Актуальность темы. Математические модели как инструменты, позволяющие исследовать сложные процессы реального мира, в том числе транспортную инфраструктуру, без капитальных затрат, являются востребованным инструментом решения многих проблем в различных сферах народного хозяйства. Развитие информационных технологий и вычислительных средств позволило расширить рамки решаемых с помощью моделей задач. Моделирование транспортных потоков необходимо потому, что активные эксперименты в существующей транспортной сети чреваты непредсказуемыми последствиями, а во многих случаях не выполнимы совсем.
Интенсивный рост автомобильного парка в городах привел к исчерпанию пропускной способности улично-дорожных сетей. Поэтому вопрос оценки эффективности организации дорожного движения в условиях высокой загрузки стал более остро, особенно для крупных и крупнейших городов. При поиске лучших стратегий управлением транспортными потоками, принятию оптимальных решений при проектировании новых объектов транспортной инфраструктуры, а также выбору рациональной организации дорожного движения необходимо принимать максимально эффективные транспортные решения.
Теория транспортных потоков обладает множеством различных моделей, однако общий уровень исследований, а также уровень практического использования моделей пока недостаточен и характеризуется определенными проблемами.
В связи с тем, что транспортные потоки нестабильны и неравномерны в течении времени, возникает проблема получения качественной и объективной информации о характеристиках транспортного потока. Проблема образования транспортных заторов в настоящее время в научной среде имеет много нерешенных вопросов, выдвигаются различные гипотезы и модели, основанные на движении жидкостей или газов, отдельных агентов, клеточных автоматов т.д. Однако, общей точки зрения в вопросе образования очередей не принято. Дорожные условия в виде резко меняющихся погодно-климатических параметров, ДТП, некачественного дорожного покрытия, ремонтных работ усложняют процесс моделирования транспортных потоков.
Таким образом, формализация движения транспортных потоков является сложным процессом и требует применения различных инструментов и технологий моделирования транспортных потоков.
Эффективным и информативным способом моделирования движения совокупности транспортных средств по магистрали являются клеточные автоматы. На основе подхода микромоделирования разработан ряд моделей, позволяющих отслеживать динамику как отдельно взятого автомобиля, так и потока в целом, и получать исходные данные для оценки времени передвижения, времени ожидания в пробке и средней скорости. Учитывая вышеизложенное можно говорить о высокой актуальности темы диссертационного исследования.
2. Цель и задачи исследования, планируемые результаты
Целью диссертационной работы является совершенствование организации дорожного движения путем применения технологии моделирования транспортного потока с помощью клеточного автомата. Для достижения поставленной цели необходимо решить следующие задачи:
- Исследовать существующие подходы к моделированию автотранспортных потоков.
- Разработать модель дорожного движения, учитывающую структуру потока автотранспорта.
- Разработать программный инструментарий для моделирования потока автомашин.
Объект исследования: транспортный поток,
Предмет исследования: математические модели транспортного потока на микроскопическом уровне.
При решении поставленных задач использовались методы:
- Компьютерного моделирования.
- Теории клеточных автоматов.
- Квантовой теории поля.
- Математической статистики..
Практическая значимость состоит в применении разработанной модели к прогнозированию дорожной ситуации.
3. Обзор исследований и разработок
3.1 Обзор международных источников
Моделирование и исследование транспортных потоков часто проводится с помощью теории конкурентного бескоалиционного равновесия, описывающего достаточно адекватный механизм функционирования автомобильных улично-дорожных сетей (УДС). Рассматриваемые модели позволяют получить прогнозные оценки по загрузке элементов транспортной сети. Подобные задачи интересны в частности тем, что являются одним из инструментов для объективной оценки эффективности проектов по модификации УДС с точки зрения разгрузки наиболее проблемных участков дорог и уменьшения общих затрат на передвижение пользователей сети.
- Модель класса Лайтхилла–Уизема–Ричардса
Первая макроскопическая (гидродинамическая) модель однополосного транспортного потока, названая впоследствии моделью Лайтхилла–Уизема–Ричардса(LWR), в которой поток АТС (вместо термина «автомобиль» и тем более «машина» в транспортной литературе принято использовать АТС) рассматривается как поток одномерной сжимаемой жидкости(часто эту модель называют моделью Лайтхилла–Уизема)[1]. В модели LWR предполагается, что:
1) существует взаимно-однозначная зависимость (уравнение состояния) между скоростью v(t,x) и плотностью (погонной) ρ(t, x) потока;
2) выполняется закон сохранения массы (количества АТС).
Запись ρ(t, x) обозначает число АТС на единицу длины в момент времени t в окрестности точки трассы с координатой x . Аналогично, v (t,x) – скорость АТС (автотранспортных средств) в момент времени t в окрестности точки трассы с координатой x.
- Модели следования за лидером (микроскопические модели)
В основе подходов кизучении микроскопических моделей лежит концепция «о желании придерживаться при движении безопасной дистанции до лидера. Одни из самых старых моделей это Реушел [2], Пайперс [3] и Форбс [4] и др. Они известны по “двухсекундному правилу”, преподававшемуся во всех автошколах. Более ранний пример это работа Херрей и Херрей, который определил безопасное расстояние следования автомобилей друг за другом, которое также включало расстояние торможения автомобиля до остановки [5]. Первые математические следующие за автомобилем модели, которые были развиты, были основаны на описании взаимодействия между двумя соседними транспортными средствами в транспортном потоке, то есть последователь и его лидер. Эта модель описывалась обычным дифференциальным уравнением для одного перегона.
Следующая модель была сделана Эди, который ввёл текущую скорость следующего транспортного средства [6]. Газис и др. работники научно-исследовательских лабораторий General Motors называли вышеупомянутый набор моделей «General Motors нелинейной моделью» или Газима-Хермана-Розери (GHR)-модель [7]. Тесно связанными с ранее обсужденными классическими моделями следования за лидером являются оптимальные скоростные модели (OVM) Ньюэлла и Бандо и др. Предыдущие модели следования за лидером главным образом описывают характеристики транспортного средства, которое cледует за лидером, OVMs изменяют механизм ускорения, такой, что желаемая скорость транспортного средства отобрана на основе пространственного перемещения, вместо того, чтобы только рассматривать скорость ведущего транспортного средства [8].
- Клеточные автоматы
Применение концепции клеточного автомата фон Неймана для моделирования транспотных потоков впервые было предложено в работе [9] . Активные разработки начались с работ Нагеля и Шрекенберга [10] . В настоящее время имется обширный набор публикаций по клеточным автоматам(см. [11]). Формулировка исходной модели Нагеля-Шрекенберга заключается в следующем [12] .
Пусть xn и vn координата и скорость n-го автомобиля, dn=xn+1-xn - дистанция до лидирующего автомобиля. Скорость может принимать одно из vmax+1 допустимых целочисленных значений vn=0, 1, 2, ...,vmax. На каждом шаге t® t+1 состояние всех автомобилей в системе обновляется в соответствии со следующими правилами:
- Ускорение. Если vn < vmax, то скорость n-го
автомобиля увеличивается на единицу, если vn=vmax, то
скорость не изменяется:
vn® min(vn+1, vmax). (1) - Торможение. Если d Ј vn, то скорость n-го автомобиля уменьшается до dn-1:
vn® min(vn, dn-1). (2) - Случайные возмущения. Если vn > 0, то скорость n-го атомобиля может быть уменьшена на единицу с вероятностью p; скорость не изменяется, если vn=0:
vn® max(vn-1, 0). (3) - Движение. Каждый автомобиль продвигается вперед на
количество ячеек, соответствующее его новой скорости после
выполнения шагов 1-3:
xn® xn+vn. (4)
3.2 Обзор национальных источников
В работе В. В. Семенов Математическое моделирование динамики транспортных потоков мегаполиса [13]. Представлены проблемы, связанные с дорожным движением мегаполисов мира и России.
Дан обзор основных идей и методов в области математического моделирования транспортных потоков. Описана математическая модель образования очереди у однополосного регулируемого перекрестка с однополосным движением.Найдена средняя длина очереди у перекрестка по данной полосе. Отмечены перспективные направления дальнейших исследований.
Долгушин Д.Ю., Мызникова Т.А. Применение клеточных автоматов к моделированию автотранспортных потоков [14]. В монографии описывается разработанная на основе теории клеточных автоматов модель автотранспортного потока, принимающая во внимание его структуру, состояние дорожного покрытия и скоростные ограничения,способная адекватно представлять ситуацию на дороге; обобщён опыт, накопленный в моделировании технических, социальных, экономических, биологических объектов с использованием клеточных автоматов.
Описаны разработанная многофакторная модель автотранспортных потоков, программный инструментарий для моделирования потоков автомашин, проведённое натурное обследование структуры и интенсивности автотранспортных потоков, а также осуществлённая на его основе калибровка модели и проверка её адекватности. С применением разработанной модели проведено моделирование практических ситуаций: исследование проблемных участков УДС г.Омска и оценка объёмов выбросов загрязняющих веществ.
Медведев Ю. Г. Моделирование движения поршня в газовой среде клеточным автоматом[15]. Обсуждаются способы задания граничных условий в многочастичной клеточно-автоматной модели потока FHP-MP. Особое внимание уделено нестационарным граничным условиям. Изложен метод перемещения стенок в исследуемой модели.
Он позволяет впервые в клеточно-автоматном моделировании потоков жидкости и газа использовать препятствия, движущиеся в процессе моделирования. Выводы подкреплены компьютерными экспериментами на примере задачи моделирования движения поршня в цилиндре, позволяющими заключить, что моделируемый процесс качественно соответствует законам физики.
4. Моделирование движения автотранспорта с помощью клеточных автоматов
Прежде чем приступить к рассмотрению моделирования движения автотранспорта с помощью клеточных автоматов необходимо понять основы теории клеточных автоматов, т.к. они входят в саму структуру данной работы.
Первые идеи о клеточных автоматах появились еще в середине ХХ века. В частности, о них говорили ученые Конрада Цузе и Джон фон Нейман, но больший вклад в развитие данной темы принадлежит Нейману[16].
По свое структуре, клеточный автомат представляет собой двухмерную сетку произвольного размера, которая состоит из ячеек и имеет произвольный размер. Стоит отметить, что состояние сетки, т.е. её конфигурация, не статична, а обновляется с течением времени, причем с некоторой зависимостью. Зависимость подразумевает то, что состояние каждой ячейки в следующий момент времени зависит от состояния ближайших её соседей. Обновление конфигурации ячеек происходит параллельно, в соответствии с правилами конкретной модели.
Каждый классический клеточный автомат обладает некоторыми свойствами. Представим их в таблице 1.
№ Название свойства Описание свойства
1 Локальность правил На новое состояние клетки могут повлиять только рядом лежащие элементы или она сама.
2 Однородность системы Ни одна область решётки не может отличаться от другой по каким-либо правилам.
3 Конечность множество возможных состояний Условие, необходимое для получение нового состояние клетки.
4 Одновременный переход в новое состояние Значение во всех клетках меняются одновременно, а не по мере вычисления.
Таблица 1 – свойства классического клеточного автомата
Таким образом, мы выделили 4 свойства, характеризующие деятельность классического клеточного автомата. Данные свойства имеют фундаментальную структуру и влияют на работоспособность самого клеточного автомата. Но, стоит отметить, что на практике не все свойства необходимо учитывать.
Например, Джон Хортон, представивший свою игру «Жизнь», показал совершенно другое виденье на использование клеточного автомата. Суть игры состоит в том, что каждая клетка должна быть или живой (закрашенной) или мертвой (пустой). Игра должна соответствовать следующим правилам:
- Не должно существовать некой начальной конфигурации, при которой возможность неограниченного роста очевидно;
- Должны существовать такие начальные конфигурации, при которых заведомо возможно создание неограниченного роста популяции;
- Должны существовать начальные простые конфигурации, для которых рост и изменение в течение значительного промежутка времени возможно.
При этом, к последнему пункты было добавлено, что их существование не должно завершаться следующим образом:
- Полным исчезновением;
- Формированием неизменной конфигурации;
- Образованием областей, повторяющим свою форму через несколько периодов.
Таким образом, финальными правилами данной игры можно назвать:
- Выживание;
- Смерть;
- Зарождение.
Такая игра по праву имеет название «Жизнь», ведь отражает многие жизненные процессы, которые так профессионально Хортон отразил в своей игре[17].
Выживание, в контексте игры, обозначает правило, при котором – клетка, с двумя или тремя соседями остается живой. Смерть же, наступает в тот момент, когда клетка обретает четыре или более соседей. При этом, клетка, находящаяся одна или с одним соседом также погибает из-за изоляции. Под зарождением имеется ввиду ситуацию, когда вокруг пустой клетки собираются три соседа. В таком случае она становится живой. В качестве примера, можно представить эволюцию трёхклеточных конфигураций по правилам игры «Жизнь», которая представлена на рисунке 1.
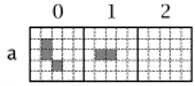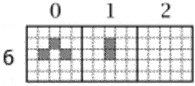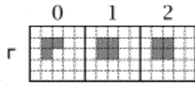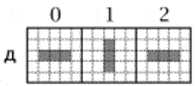
Эволюция трехклеточных конфигураций по правилам игры «Жизнь» (анимация: 5 кадров, 8 циклов повторения, 21 килобайт) Работы Джона Хортона интересовали все научное сообщество на протяжении десятилетий. Различные исходы конфигураций позволяли исследователям делать некоторые выводы, поэтому им давали целые названием. Например, популярными конфигурациями стали: улей, блок, озеро, лодка, мигалка , маяк, пульсатор, космический корабль и многие другие.
Особенностью данных фигур является их устойчивость или периодичность. Некоторые из них оставались неизменными, а некоторые повторяли свою форму через несколько периодов. Наиболее известным примером периодической формы является глайдер, который принимал свою изначальную форму через 4 периода.
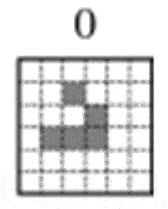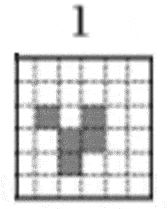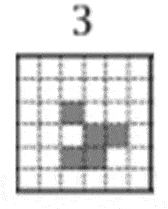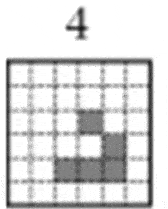
Эволюция глайдера(анимация: 5 кадров, 8 циклов повторения, 36 килобайт) Здесь стоит упомянуть работу Пола Чепменома, который, на основе изучения игры «Жизнь» сделал целое открытие. Он предложил некоторую конфигурацию, способную теоретически производить вычисления любой сложности, что в дальнейшем получила дальнейшее развитие. На этом изучение теории клеточных автоматов не закончилось. Следующий яркий период его становления возглавил Стивен Вольфрам в 80х годах двадцатого века. Используя большой пласт работ с использованием вычислительной техники, Вольфрам представил классификацию клеточных автоматов, с точки зрения математических моделей самоорганизующихся систем.
Таким образом, изучение и формирование теории клеточных автоматов происходило постепенно и имело ряд нескольких взлетов и научных открытий. Благодаря высокому интересу к данной теме, ей посвятили свои труды многие авторы, включая Неймара, Нагеля, Шрекенберга и многих других известных ученых и авторов того времени. Позже, в моделировании транспортных потоков клеточные автоматы получили особое название – транспортные клеточные автоматы, сокращенно ТКА.
Выводы
Моделирование и исследование транспортных потоков часто проводится с помощью теории конкурентного бескоалиционного равновесия, описывающего достаточно адекватный механизм функционирования автомобильных улично-дорожных сетей (УДС). Рассматриваемые модели позволяют получить прогнозные оценки по загрузке элементов транспортной сети. Подобные задачи интересны в частности тем, что являются одним из инструментов для объективной оценки эффективности проектов по модификации УДС с точки зрения разгрузки наиболее проблемных участков дорог и уменьшения общих затрат на передвижение пользователей сети.
Основными эмпирическими свойствами перехода к плотному транспортному потоку являются:
- Переход к плотному транспортному потоку (traffic breakdown) является F>S переходом (буква F соответствует «free flow», т.е. свободному потоку, буква S обозначает фазу синхронизованного потока, в английской литературе «synchronized flow»).
- Вероятность спонтанного F>S перехода является растущей функцией величины потока.
Может быть как спонтанный, так и индуцированный (т.е. вызванный внешним возмущением большой амплитуды) F>S переход около одного и того же узкого места на дороге (bottleneck в англоязычной литературе).
Рассмотрено применение клеточных автоматов при моделировании движения автотранспорта. Исследования транспортных потоков проводились на протяжении десятилетий, что в итоге, дало множество полезных данных для исследования. Каждая из моделей имеет свои достоинства и недостатки, которые определяют оптимальную зону её применения.
Список источников
- Lighthill M.J., Whitham G.B. On kinematic waves / Proc. R. Soc.Lond. Washington, D.C.: Highway Research Board, National Research Counsil,1964. Vol. 1-3.
- Reuschel A. Fahrzeugbewegungen in der kolonne bei gleichfoermigbeschleunigte moder verzoegtem leifahrzeug // Z. Oesterr. Ingr.Architekt. Vereines, 1950. P.59–62,73–77.
- Pipes L.A. An operational analysis of traffic dynamics // Journal of Applied Physics, 1953. № 24(3). P. 274– 281.
- Forbes T.W. Measurement of driver reactions to tunnel conditions // In Proceedings of the Highway Research Board, 1958. Vol. 37. P. 345–357.
- Herrey E.M.J., Herrey H. Principles of physics applied to trafficmovements and road conditions // American Journal of Physics. 1945. №13. P. 1–14.
- Edie L.C. Car following and steady-state theory for non-congested traffic // Operations Research, 1961. №9. P. 66–76.
- Gazis D., Herman R., Rothery R. Nonlinear follow-the-leader models of traffic flow// Operations Research, 1961. №9. P. 545–567.
- Helbing D. Traffic and related self-driven many-particle systems // Reviews of Modern Physics October. 2001. №73. P. 1067–1141.
- Cremer M., Ludwig J. A fast simulation model for traffic flow on the basis of Boolean operations // Math. Comp Simul. -- 1986. -- V. 28. -- P. 297-303.
- Nagel K., Schreckenberg M. A cellular automation model for freeway traffic // J. Phys. I France. -- 1992. -- Vol. 2. -- P. 2221-2229.
- Chowdhury D., Santen L., Schadschneider A. Statistical physics of vehicular traffic and some related systems // Phys. Rep. -- 2000. -- Vol. 329. -- P. 199-329.
- Швецов В.И. Математическое моделирование транспортных потоков // Автоматика и телемеханика. -- 2003. -- 11.
- Медведев Ю. Г. Моделирование движения поршня в газовой среде клеточным автоматом / Ю. Г. Медведев // Прикладная дискретная математика. – 2010. – №4(10). – С. 100 – 108.
- Семенов В.В. Математическое моделирование динамики транспортныхпотоков мегаполиса – М., 2004. – 44 с.
- Долгушин Д. Ю. Многофакторная модель дорожного движения города на основе клеточных автоматов / Д. Ю. Долгушин, Т. А. Мызникова // Материалы 62-й научно-технической конференции СибАДИ. – Омск: СибАДИ, 2008. – С. 109 – 113.
- Нейман Д., фон. Теория самовоспроизводящихся автоматов / закончено и отред. [предисловие и введ., с. 40–48, написаны] А. В. Бёрксом: пер. с англ. В. Л. Стефанюка; под ред. В.И. Варшавского. – М.: Мир, 1971. – 384 с.
- Gardner M. Mathematical Games: The fantastic combinations of JohnConway’s new solitaire game “Life” // Scientific American. 1970.–October. Vol. 223, no. 4. Pp. 120–123.
- Ускорение. Если vn < vmax, то скорость n-го
автомобиля увеличивается на единицу, если vn=vmax, то
скорость не изменяется:
