Реферат за темою випускної роботи
Увага! На момент написання цього реферату магістерська робота ще не завершена. Передбачувана дата завершення – травень 2022 р. Повний текст роботи, а також матеріали на тему можуть бути отримані у автора або його наукового керівника після вказаної дати.
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Основні закони (принципи) квантової механіки
- 4. Наближення Борна-Опенгеймера
- 5. Теорема Яна-Телера
- 6. Наближення самоузгодженого поля
- Перелік посилань
Введение
У завданнях, що відносяться до будови, геометрії, до коливальних та електронних спектрів молекул методи дослідження, що ґрунтуються на законах класичної фізики, не застосовні. Для систем нано та меншого розміру у першій третині 20-го століття була розвинена квантова теорія, квантова механіка [1]. Її основне рівняння, рівняння Шредінгера, точно вирішується для одно-і двох-часткових систем з урахуванням їхньої взаємодії. Вже для трьох часткових систем таких рішень немає.
Для багатьох часткових систем були розвинені наближені методи вирішення рівняння Шредінгера, засновані на
застосуванні пробної хвильової функції певного виду з мінімізацією значення функціоналу енергії за
вільними
параметрами для кожної наближеної хвильової функції. При цьому в квантовій теорії атома
враховувалася
його
сферична симетрія як для кожної атомної орбіталі, так і для часткової хвильової функції атома застосуванням
коефіцієнтів Клебша-Гордана і для просторової, і для її спинової частини. А вимога певного орбітального і
спинового моментів багато часткового стану вело до врахування взаємодії обмеженого числа електронних змін. У
квантовій теорії молекул широке застосування знайшли методи Хартрі-Фока, необмежений або обмежений спиною,
що спирається на пробну хвильову функцію у формі детермінанта зі спін-орбіталей.
1. Актуальность темы
Варто відзначити, що проблема узгодження просторової симетрії молекули для хвильової функції, з певною її просторовою і спиновою симетрією враховується введенням обмеженої конфігураційної взаємодії, а усереднення вироджених молекулярних станів у ряді випадків допускає, до того ж, і збереження матричної форми запису функціоналу без точного доказу в [13]. Функціонал енергії електронів для таких наближених, пробних хвильових функцій будується при фіксованому положенні ядер, що відображає симетрію молекули, і потім мінімізується.
Застосування до цього функціоналу варіаційного принципу, коли величинами, що варіюються, є молекулярні орбіталі, дає рівняння для їх обчислення. Особливість цих рівнянь у тому нелінійності.
У модельному сенсі електрон на молекулярній орбіталі, що визначається з цих рівнянь, знаходиться в усередненому полі, створюваному електронами на тих самих, невідомих поки що, молекулярних орбіталях.
Спосіб розв'язання таких рівнянь ітераційний. Його результат залежить, звісно, від геометрії початкового наближення для молекулярної орбіталі. За наявності виродження МО на порозі нестабільності, розвиненою в інваріантному матричному формулюванні М. М. Местечкіним, можлива поява нових рішень. Як рішення рівняння нестабільності, вони можуть зароджуватися за різними принципами. Це або відгалуження від відомого рішення, що має ту ж симетрію, або зародження нового, можливо, і несиметричного рішення.
Для вироджених електронних станів характерною є наявність ефекту Янна-Теллера. Проте
конфігураційна нестабільність фізично індукується не виродженням електронних станів, а скоріш не
симетричним розподілом зарядів на довільному виродженому стані
. Для лінійного рівняння Шредінгера
хвильова функція належить неприведеному уявленню точкової групи молекули, тобто узгоджується з симетрією
ядерного остова. Інша ситуація для нелінійних рівнянь Хартрі-Фока. Тут спонтанне порушення симетрії на
порозі нестабільності цікавить пояснення фізичної природи ефекту Янна-Теллера для молекул у наближенні
Хартри-Фока.
2. Цель и задачи исследования, планируемые результаты
Завданням роботи є знаходження рівнянь нестабільності додаткових рішень із зниженою симетрією. При цьому пріоритетним завданням є пошук таких ситуацій, коли нестабільності, що з'являються, є універсальними, тобто що з'являються в спочатку симетричній молекулярній системі. Пошук таких рішень буде проводиться в МО ЛКАО-наближенні в обмеженому методі Хартрі-Фока для систем, що мають вісь симетрії 3-го порядку. Передбачається наявність таких систем універсальної нестабільності з порушенням зазначеної симетрії, що дозволить обговорити межі її застосовності.
Однією з додаткових завдань є якісна візуалізація отриманих результатів малюнками енергетичних поверхонь, що визначаються теорією збурень на порозі несиметричного рішення, що зароджується. Наявність зародження несиметричних рішень з нижчою енергією змінить і симетрію потенціалу для ядер, що призведе до зміни просторової симетрії та самої молекули.
3. Основні закони (принципи) квантової механіки
Наприкінці 19-го століття накопичилася низка експериментальних фактів: закон Кірхгофа для теплового випромінювання абсолютно чорного тіла, закономірності фотоефекту, лінійних спектрів атомів і молекул, відсутність різниці у швидкості світла вздовж напрямку руху Землі та поперек її. І жоден із них не знаходив пояснення в рамках добре розвиненої на той час класичної механіки та електродинаміки.
Першими кроками до створення квантової теорії були гіпотеза Планка про квантування випромінювання та гіпотеза Луї-де-Бройля про хвильові властивості речовини. Робота Борна, Шредінгера, Гейзенберга та Дірака завершили створення математичної моделі квантової механіки у 20-х роках 20-го століття. У її основі лежить ряд постулатів, принципів, які можуть бути виведені чи обгрунтовані теоретично [1-3].
Дуалізм Луї-де-Бройля, хвиля-частка
, принципово відрізняє мікрочастинку, нано частинку, від звичних
нам
частинок та від звичних нам хвиль. Для нано частки втрачає сенс поняття траєкторії, оскільки рух траєкторією
не сумісний з властивим їй явищем дифракції та інтерференції. Але сьогодні всі принципи (закони) квантової
механіки (її математична модель) цілком експериментально підтверджені.
У квантовій механіці (КМ) руху вільної частинки з імпульсом p у вакуумі зіставляють плоску монохромічну хвилю, функцію:
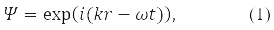
де з гіпотези де Бройля
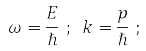
E – енергія частки, ℏ = 1,05*10-34Дж·с – постійна Планка та |p| = 2π/α, α – довжина хвилі де Бройля.
Загалом замість (1) хвильову функцію записують
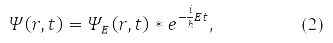
Для хвильової функції (2) в 1926 Макс Борн запропонував імовірнісне трактування, за якою |ψ(r,t)|2 визначає щільність ймовірності для частки бути виявленою в момент часу t на околиці точки r
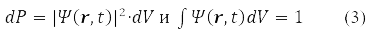
Постулат (3) узагальнюється довільне число частинок системи. Досвід показав, що елементарні частинки мають спину і в ψ(r,σ,t) включили спінові змінні, σ = α коли проекція спина на вісь OZ равна 1/2 и σ = β, коли проекція дорівнює -1/2. Стверджується, що вольова функція містить максимальний, досяжний обсяг інформації про систему, яку можна отримати у КМ. При цьому принцип Паулі [1-4] вимагає, щоб для частинок з напівцілим спином їхня хвильова функція була антисиметричною щодо перестановки всіх координат будь-якої пари таких частинок.
Рисунок 1 – Обертання молекули
(анімація: 7 кадрів, 5 циклів повторення, 138
кілобайт)
Другий принцип квантової механіки (КМ) – це принцип суперпозції. По ньому система, яка може перебувати у станах із хвильовими функціями (ВФ) ψ1,ψ2,…,ψk, може перебувати й у стані
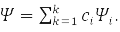
За третім принципом КМ кожній спостережуваній величині зіставляється лінійний ермітовий оператор, наприклад:
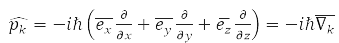
– оператор імпульсу k-ої частинки
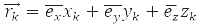
– оператор координат k-ой частинки, оператор її енергії:
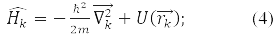
Ппро четвертий принцип допустимими значеннями, які можуть бути отримані при вимірюванні фізичної величини А, є власні значення лінійного ермітового оператора цієї величини. Наприклад, у стані ψE(rk), що відповідає власному значенню E оператора Гамільтона:
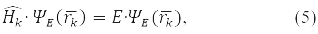
спостерігається значення енергії k-ой частинки рiвно Е.
У формулах (4) і (5) враховано і 5-й постулат, принцип, КМ: оператор будь-якої фізичної величини, що має класичний аналог, може бути знайдений за формулами класичної фізики, якщо в них замінити координати на імпульси на відповідні їм оператори.
Наслідком 4-го і 5-го постулатів слід твердження, що дві фізичні величини можуть бути виміряні одночасно (з як завгодно високою точністю) тоді і тільки тоді, коли комутують їх оператори. Тоді ці оператори мають однакові власні функції.
З факту, що комутують однакові проекції радіус вектора частки та її імпульсу, [x,px]=[y,py]=[z,pz]=0, слід, що відповідні проекції не виміряні одночасно, тобто, що точніше вимірюється одна з них, тим більше невизначеною стає друга з них.
ейзенберг записав цей результат як співвідношення невизначеності:
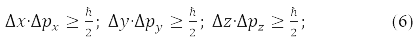
Проте відбиває те що, що з мікрочастинок (наночастинок) відсутні траєкторії.
Всі проекції оператора кутового моменту не комутують один з одним, але кожна комутує з оператором квадрата кутового моменту. Тому одночасно можна виміряти лише квадрат кутового моменту та одну (будь-яку) його проекцію.
Шостий принцип КМ відповідає питанням: Як шукати хвильову функцію стану квантовомеханической системи, на
яку хвильові властивості речовини істотні?
Відповідь це питання 1926 року дав Е. Шредінгер. Він записав рівняння, якому задовольняє функція хвилі
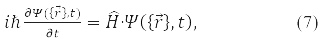
где
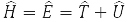
– оператор енергії системи (оператор Гамільтоніана), T – оператор кінетичної енергії та U – оператор потенційної енергії її частинок. Формула (5) записана для хвильової функції частки у стаціонарному (незалежному від часу) стані. Рівняння (7) називають рівнянням Шредінгера.
4. Наближення Борна-Опенгеймера
Вся інформація про квантовомеханічну систему міститься у вирішенні рівняння (7). При його вирішенні враховують максимальне число комутирующих операторів фізичних величин, що описують стан системи, включаючи оператор Гамільтона, щоб хвильова функція була для них власною і для отриманого стану всі ці величини, включаючи енергію, були виміряні, як завгодно точно.
Рівняння (7) точно вирішується для частинки у потенційному полі [1, 3] та для двох взаємодіючих частинок. Завдання для них спрощується переходом до координат центру мас і відносної відстані між частинками: r:
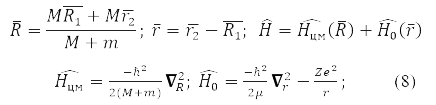
де
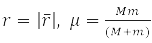
– наведена маса взаємодіючих частинок.
У цих координатах завдання (7) факторизується
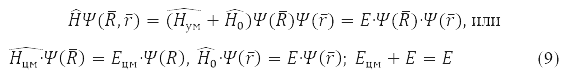
Рішення
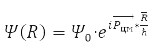
визначає вільний рух центру мас.
Завдання для відносного радіусу
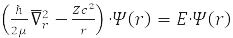
має сферичну симетрію і вирішується поділом змінних у сферичних координатах при виборі системи комутувальних операторів: проекція кутового моменту на вісь OZ, LZ, квадрата кутового моменту L2, та енергії H0. Для атома водню М – маса протона та m – електрона,
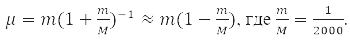
Тобто з точністю до 0,05% можна вважати, що μ=m і електрон рухається у полі нерухомого ядра [1-4].
Для трьохчасткового завдання вже немає точного рішення, а є чисельні рішення рівняння Фадєєва [5], в основному для завдання тричастинного розсіювання з узагальненнями на розсіювання більшої кількості частинок.
Тому багаточасткове завдання вирішується приблизно. Для атомів і молекул наближений поділ руху електронів та ядер ґрунтується на зазначеному вище співвідношенні їх мас,
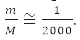
Для вирішуваного у разі багатоелектронної завдання у полі нерухомих ядер атомів молекули теж розвинені наближені методи: від конфігураційного взаємодії до різних методів самоузгодженого поля, засновані на застосуванні варіаційного методу [4].
Вперше поділ електронного та ядерного рухів було проведено у роботі Борна та Оппенгеймера. [6].
Якщо відволіктися від поступального руху молекули як цілого, то по порядку їх значень можна виділити три види руху – рух електронів у полі ядер, коливання ядер щодо центру мас молекули, які рухаються повільно проти електронами в усередненому їх полі, і обертань молекули навколо осей, що надходить через центр мас. При цьому, Eел.мол ≫ Eел.мол ≫ Eел.мол, та повна енергія молекули: E = Eел. + Eкол. + Eвр. У цьому наближенні ψ = ψэл. + ψкол. + ψвр.. Кожному фіксованому положенню ядер відповідає певна енергія Eэл.({R}). У цьому вся сенсі електронна енергія, як функція межядерных відстаней, грає самих ядер роль потенційної енергії. Для стійких багатоатомних молекул отримано простий критерій застосування наближень Борна-Оппенгеймера:
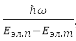
де ω – найбільша з циклічних частот нормальних коливань ядер поблизу точок рівноваги, Eэл.п и Eэл.т – енергії сусідніх електронних станів.
5. Теорема Яна-Телера
У 1937 році Ян і Теллер довели теорему, що обмежує можливі зміни для ядер атомів у нелінійних молекулярних систем. Її доказ заснований на теорії збурень для вироджених електронних станів симетричної молекули щодо зміщень атомів молекули за нормальних її коливань, класифікованих за неприведеними уявленнями групи симетрії молекули. Для всіх молекул, крім лінійних, її доказ заснований на наявності в розкладанні квадрата неприведеного уявлення її виродженого електронного стану будь-якого неприведеного уявлення з можливих для нормальних коливань молекули (див. стор. 209-226 в [7]).
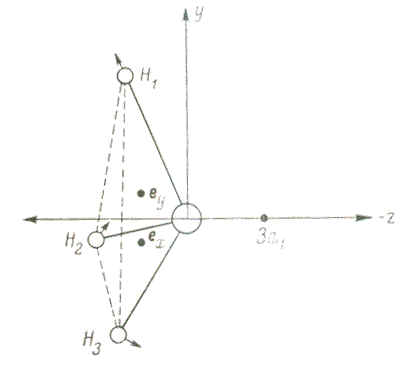
Рисунок 2 — Ян-теллерівські зрушення в молекулі BH3
У 1959 році Клінтон і Райс спираючись на теорему Гельмана-Фейнмана дали нове обґрунтування для теореми
Яна-Теллера, фізична суть якого пов'язана з силовим впливом заряду хмари електронів
в основному
виродженому співвідношенні молекули (визначається їх щільністю) кожного атома. На прикладі молекул симетрії
D3h и D4h вони показали можливість стабілізації для них несиметричної
геометрії, яку можуть спричинити коливання ядер із симетрією B1g и B2g
(див. стор. 379-389 в [7]).
Варто зазначити, що лінійне рівняння Шредінгера при симетричному розташуванні ядер молекули має рішення,
що належить неприведеному уявленню групи симетрії такої молекули. Якщо її основне електронне
стан вироджений, то при реалізації одного з компонентів стану його електронна щільність виявляється не
симетричною і сила їхньої кулонівської взаємодії з повільними ядрами
, у зазначених Яном та Теллером
Випадки можуть призвести до зниження симетрії молекули. Внаслідок лінійності рівняння (7) це позначиться і
на його вирішенні для хвильової функції електронів, симетрія якої теж знизиться і, в результаті, виродження
основного стану зніметься.
6. Наближення самоузгодженого поля
Хвильова функція для багатоелектронної задачі визначається рішенням рівняння Шредінгера (7) в наближенні Борна-Оппенгеймера при нерухомих ядрах. Спінові взаємодії зазвичай враховуються з теорії збурень.
Неможливість точного розв'язання рівняння (7) призвела до розвитку наближених методів, заснованих на мінімізації середнього значення Гамільтоніана, обчисленого для певної пробної функції. Коли вона представлена у вигляді розкладання по детермінантах зі спинорбіталей, взятих з певного базису, маємо спосіб конфігураційної взаємодії (КВ) [8,9]. Вимога антисиметрії хвильової функції, як сказано вище, випливає із принципу Паулі. Методи КВ засновані на базисі власних функцій одноелектронного Гамільтоніана дозволяють класифікувати енергетичні рівні, але є практично зручними для розрахунків.
Найефективнішим є метод самоузгодженого поля Хартрі-Фока. Метод Хартрі не враховував принцип Паулі. А Фок виправив його, записавши замість твору орбіталей детермінант із них. Одержувані з варіаційного принципу для молекулярних орбіталей такої функції рівняння суттєво нелінійні. Для них отримано і орбітальний запис [1-4] та матрична форма [10]. У разі функціонал енергії у спин орбітальному вигляді [11] записується так:
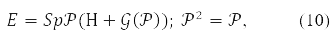
де будь-яка з матриць P,H,𝒢(P), в (9) розкладається за матрицями Паулі, що діють у спиновому просторі
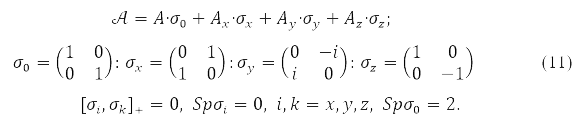
Функціонал (9), як окремі випадки, включає: і наближення різні орбіталі для різних спинів (РОРС), так званий необмежений метод Хартрі-Фока (НХР), і наближення з двома кратним заповненням орбіталей замкнутої оболонки – обмежений метод Хартрі-Фок (ОХФ). У НХФ методі певне значення має лише проекція спина, а ОХФ методі і повний спин електронів, та її проекція.
Замість одноелектронної щільності в задачах із застосуванням 1-ї та 2-ї варіації функціоналу енергії, δE та δ2E, зручно застосовувати інволютивну матрицю:
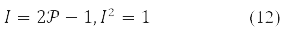
З нею функціонал (9) набуває вигляду:
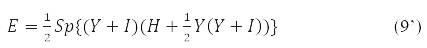
та умова стаціонарності
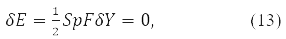
де
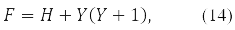
дає рівняння:
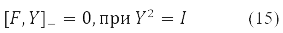
Подальше варіювання енергії
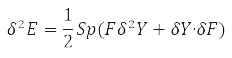
з урахуванням властивостей ступенів Y-матриці остаточно дає значення:
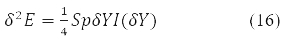
Де δY = D – матриця варіації інволютивної матриці, підпорядкованої умові
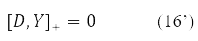
Вариация D преобразуется в (15) в новую эрмитовую матрицу I(D) согласно правилу [11].
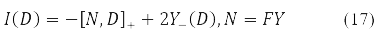
Компактний спин орбітальний вид рівнянь Хартрі-Фока (14) та другої варіації енергії (15)-(16) стають можливими завдяки матричному [10] запису та функціоналу енергії, і 1-ї та 2-ї його варіації.
У випадку δ2E ≤ 0 отримуємо умову нестабільності розв'язання рівнянь (14) для стаціонарного стану. Цій ситуації відповідає не позитивні власні значення оператора стабільності (16)
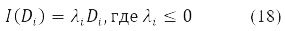
З форми запису рівнянь (14)-(17) можна витягти як різні варіанти методу Хартри-Фока, а й розглянути його нестабільності щодо різного виду матриць Д, як без перевороту спина і з переворотом спина. В роботі [12], наприклад, доведено універсальну нестабільність обмеженого методу Хартрі-Фока (ОХФ) щодо варіації орбіталей (і відповідно матриці Д) з переворотом спина для стану з довільними повним спином.
Різні методи Хартрі-Фока отримав за певних вимог на розкладність (10) щільності У за матрицями Паулі. Так, ОХФ методу із замкнутою оболонкою відповідає Y = Y0δ0 при Y2 = 1, рівняння самоузгодженого поля
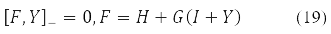
де
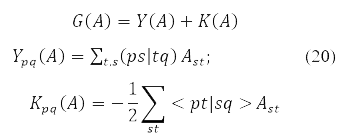
та функціонал енергії
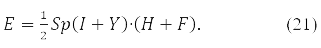
В (19) <qt|qs> – інтеграл 2-х часткової кулонівської взаємодії електронів
на
орбітах xp,xt,xq,xs.
Перелiк джерел
- Ландау Л.Д. Теоретическая физика. Т. 3: Квантовая механика / Л.Д. Ландау, Е.М. Лифшиц. – 5-е изд. – М.: Физматлит, 2002. – 767 с.
- Мессиа А. Квантовая механика. Т.1 / А. Мессиа. – М.: Наука, 1978. – 478 с.
- Мессиа А. Квантовая механика. Т.2 / А. Мессиа. – М.: Наука, 1979. – 584 с.
- Соколов И.М. Квантовая химия: учеб. пособие / И.М. Соколов. – СПб.: Изд-во Политехн. ун-та, 2010. – 122 с.
- Шмид Э., Цигельман Х. Проблема трёх тел в квантовой механике, монография, перев. с англ. – М.: Наука, 1979, – 272 с.
- Born M., Oppenheimer J.R., Ann. Physik, 1927, V.84, – p. 45
- Нокс Р. и Голд А. Симметрия в твёрдом теле. – М.: Наука, 1970. – 424 с.
- Foresman J. B., Нead-Gordon М., Pople J. A., Frisch М. J. J. Phys. Chem., 1992, v. 96, р. 135.
- Head-Gordon M., Rico R.J., Oumi M., Lee T.J. – Chem. Phys. Jett., 1994, V.219, p. 21
- Местечкин М. М. Метод матрицы плотности в теории молекул. – Киев: «Наукова думка», 1977. – 352 с.
- Местечкин М.М. Нестабильность уравнений Хартри-Фока и устойчивость молекул. – Киев: «Наукова думка», 1986. – 176 с.
- Mestechkin M.M., Klimko G.T., Whyman G.E. On the universal instability of the open-shell Restricted Hartry-Fock method. // Chem. Phys. Lett. – 1985. – V. 115, № 6. – 531 – 534.
- Roothaan C. C. J. Self-Consistent Field Theory for Open Shells of Electronic Systems. – Rev. Mod. Phys., 1960. V. 32, P. 179 – 186.
