Реферат по теме выпускной работы
Внимание! На момент написания данного реферата магистерская работа ещё не завершена. Предполагаемая дата завершения – май 2022 г. Полный текст работы, а также материалы по теме могут быть получены у автора или его научного руководителя после указанной даты.
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Основные законы (принципы) квантовой механики
- 4. Приближение Борна-Оппенгеймера
- 5. Теорема Яна-Теллера
- 6. Приближение самосогласованного поля
- Список источников
Введение
В задачах, относящихся к строению, геометрии, к колебательным и электронным спектрам молекул методы исследования, основанные на законах классической физики, не применимы. Для систем нано и меньшего размера в первой трети 20-го века была развита квантовая теория, квантовая механика [1]. Её основное уравнение, уравнение Шредингера, точно решается для одно- и двух- частичных систем с учётом их взаимодействия. Уже для трёх частичных систем такие решения отсутствуют.
Для много частичных систем были развиты приближённые методы решения уравнения Шрёдингера, основанные на
применении пробной волновой функции определённого вида с минимизацией значения функционала энергии по
свободным
параметрам для каждой приближённой волновой функции. При этом в квантовой теории
атома
учитывалась его сферическая симметрия как для каждой атомной орбитали, так и для много частичной волновой
функции атома применением коэффициентов Клебша-Гордана и для пространственной, и для
спиновой её
части. А требование определённого орбитального и спинового моментов много частичного состояния вело к учёту
взаимодействия ограниченного числа электронных конфигураций.
В квантовой теории молекул широкое применение нашли методы Хартри-Фока, неограниченный или ограниченный по
спину, опирающийся на пробную волновую функцию в форме детерминанта из спин-орбиталей.
1. Актуальность темы
Стоит отметить, что проблема согласования пространственной симметрии молекулы для волновой функции, с определённой её пространственной и спиновой симметрией учитыется введением ограниченного конфигурационного взаимодействия, а усреднение вырожденных молекулярных состояний в ряде случаев допускает, к тому же, и сохранение матричной формы записи функционала энергии, как предполагалось без точного доказательства в [13]. Функционал энергии электронов для таких приближенных, пробных, волновых функций строится при фиксированном положении ядер, отражающем симметрию молекулы, и затем минимизируется.
Применение к этому функционалу вариационного принципа, когда варьируемыми величинами являются молекулярные орбитали, даёт уравнения для их вычисления. Особенность этих уравнений в их нелинейности.
В модельном смысле электрон на молекулярной орбитали, определяемой из этих уравнений, находится в усредненном поле, создаваемом электронами на этих же, неизвестных пока, молекулярных орбиталях.
Способ решения таких уравнений итерационный. Его результат зависит, естественно, от геометрии начального приближения для молекулярной орбитали. При наличии вырождения МО на пороге нестабильности, развитой в инвариантной матричной формулировке М. М. Местечкиным, возможно появление новых решений. Являясь решением уравнения нестабильности, они могут зарождаться по разными принципам. Это или ответвление от известного решения, имеющее ту же симметрию, или зарождение нового, возможно и несимметричного решения.
Для вырожденных электронных состояний характерно наличие эффекта Янна-Теллера. Тем
не менее
конфигурационная нестабильность физически индуцируется не собственно вырождением электронных состояний, а
скорее не симметричным распределением зарядов на произвольном вырожденном состоянии
. Для
линейного
уравнения Шредингера волновая функция принадлежит неприводимому представлению точечной группы молекулы, то
есть согласуется с симметрией ядерного остова. Иная ситуация для нелинейных уравнений Хартри-Фока. Здесь
спонтанное нарушение симметрии на пороге нестабильности представляет интерес для
объяснения физической
природы эффекта Янна-Теллера для молекул в приближении Хартри-Фока.
2. Цель и задачи исследования, планируемые результаты
Задачей работы является нахождение для уравнений нестабильности дополнительных решений с пониженной симметрией. При этом приоритетной задачей является поиск таких ситуаций, когда появляющиеся нестабильности являются универсальными, то есть появляющимися в изначально симметричной молекулярной системе. Поиск таких решений будет проводится в МО ЛКАО-приближении в ограниченном методе Хартри-Фока для систем имеющих ось симметрии 3-го порядка. Предполагается наличие для таких систем универсальной нестабильности с нарушением указанной симметрии, что позволит обсудить границы её применимости.
Одной из дополнительных задач является качественная визуализация полученных результатов рисунками энергетических поверхностей, определяемых теорией возмущений на пороге зарождающегося несимметричного решения. Наличие зарождения несимметричного решений с более низкой энергией изменит и симметрию потенциала для ядер, что приведёт к изменению пространственной симметрии и самой молекулы.
3. Основные законы (принципы) квантовой механики
В конце 19-го века накопился ряд экспериментальных фактов: закон Кирхгофа для теплового излучения абсолютно черного тела, закономерности фотоэффекта, линейчатых спектров атомов и молекул, отсутствие разности в скорости света вдоль направления движения Земли и поперек её. И ни один из них не находил объяснение в рамках хорошо развитой к тому времени классической механики и электродинамики.
Первыми шагами к созданию квантовой теории были гипотеза Планка о квантовании излучения и гипотеза Луи-де-Бройля о волновых свойствах вещества. Работа Борна, Шредингера, Гейзенберга и Дирака завершили создание математической модели квантовой механики в 20-х годах 20-го века. В её основе лежит ряд постулатов, принципов, которые не могут быть выведены или обоснованы теоретически [1-3].
Дуализм Луи-де-Бройля, волна-частица
, принципиально отличает микрочастицу, нано частицу, от привычных
нам
частиц и от привычных нам волн. Для нано частицы теряет смысл понятие траектории, так как движение по
траектории не совместимо с присущим ей явлением дифракции и интерференции. Но сейчас все принципы (законы)
квантовой механики (её математическая модель) полностью экспериментально подтверждены.
В квантовой механике (КМ) движению свободной частицы с импульсом p в вакууме сопоставляют плоскую монохромическую волну, функцию:
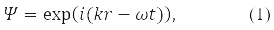
где по гипотезе де Бройля
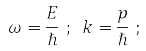
E – энергия частицы, ℏ = 1,05*10-34Дж·с – постоянная Планка и |p| = 2π/α, α – длина волны де-Бройля.
В общем случае вместо (1) волновую функцию записывают
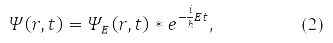
Для волновой функции (2) в 1926 году Макс Борн предложил вероятностную трактовку, по которой |ψ(r,t)|2 определяет плотность вероятности для частицы быть обнаруженной в момент времени t в окрестности точки r
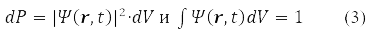
Постулат (3) обобщается на произвольное число частиц системы. Опыт показал, что элементарные частицы обладают спином и в ψ(r,σ,t) включили спиновые переменные, σ = α когда проекция спина на ось OZ равна 1/2 и σ = β, когда проекция равна -1/2. Утверждается, что волвая функция содержит максимальный, достижимый объем информции о системе, которую о ней можно получить в КМ. При этом принцип Паули [1-4] требует, чтобы для частиц с полуцелым спином их волновая функция была антисимметричной относительно перестановки всех координат любой пары таких частиц.
Рисунок 1 – Вращение молекулы
(анимация: 7 кадров, 5 циклов повторения, 138
килобайт)
Второй принцип квантовой механики (КМ) – это принцип суперпозции. По нему система, которая может находиться в состояниях с волновыми функциями (ВФ) ψ1,ψ2,…,ψk, может находиться и в состоянии
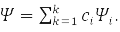
По третьему принципу КМ каждой наблюдаемой величине сопоставляется линейный эрмитовый оператор, например:
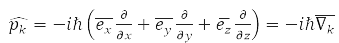
– оператор импульса k-ой частицы
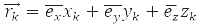
– оператор координат k-ой частицы, оператор её энергии:
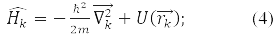
По четвертому принципу допустимыми значениями, которые могут быть получены при измерении физической величины А, являются собственные значения линейного эрмитового оператора этой величины. Например, в состоянии ψE(rk), отвечающей собственному значению E оператора Гамильтона:
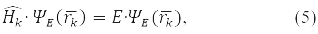
наблюдаемое значение энергии k-ой частицы равно Е.
В формулах (4) и (5) учтен и 5-й постулат, принцип, КМ: оператор любой физической величины, имеющей классический аналог может быть найден по формулам классической физики, если в них заменить координаты на импульсы на соответствующие им операторы.
Следствием 4-го и 5-го постулатов следует утверждение, что две физические величины могут быть измерены одновременно (со сколь угодно высокой точностью) тогда и только тогда, когда коммутируют их операторы. Тогда у этих операторов одинаковые собственные функции.
Из факта, что коммутируют одинаковые проекции радиус вектора частицы и её импульса, [x,px]=[y,py]=[z,pz]=0, следует, что соответствующие проекции не измеримы одновременно, то есть, чем точнее измеряется одна их них, тем более неопределённой становится вторая из них.
Гейзенберг записал этот результат в виде соотношения неопределенности:
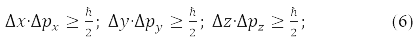
Оно отражает тот факт, что у микрочастиц (наночастиц) отсутствуют траектории.
Все проекции оператора углового момента не коммутируют друг с другом, но каждая из них коммутирует с оператором квадрата углового момента. Поэтому одновременно можно измерить лишь квадрат углового момента и одну (любую) его проекцию.
Шестой принцип КМ отвечает на вопрос: Как находить волновую функцию состояния квантовомеханической
системы, для которой волновые свойства вещества существенны?
Ответ на этот вопрос в 1926 году дал Э. Шредингер. Он записал уравнение, которому удовлетворяет волновая функция
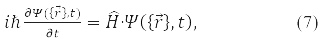
где
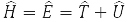
– оператор энергии системы (оператор Гамильтониана), T – оператор кинетической энергии и U – оператор потенциальной энергии её частиц. Формула (5) записана для волновой функции частицы в стационарном (независимом от времени) состоянии. Уравнение (7) называют уравнением Шредингера.
4. Приближение Борна-Оппенгеймера
Вся информация о квантовомеханической системе содержится в решении уравнения (7). При его решении учитывают максимальное число коммутирующих операторов физических величин, описывающих состояние системы, включая оператор Гамильтона, чтобы волновая функция была для них собственной и для полученного состояния все эти величины, включая, энергию, были измеримы, сколь угодно точно.
Уравнение (7) точно решается для частицы в потенциальном поле [1, 3] и для двух взаимодействующих частиц. Задача для них упрощается переходом к координатам центра масс и относительного расстояния r между частицами:
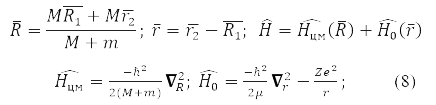
где
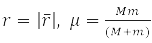
– приведенная масса взаимодействующих частиц.
В этих координатах задача (7) факторизуется
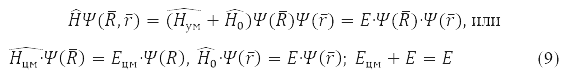
Решение
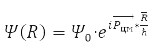
описывает свободное движение центра масс.
Задача для относительного радиуса
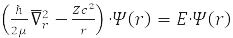
обладает сферической симметрией и решается разделением переменных в сферических координатах при выборе системы коммутирующих операторов: проекция углового момента на ось OZ, LZ, квадрата углового момента L2, и энергии H0. Для атома водорода М – масса протона и m – электрона,
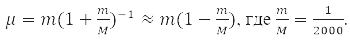
То есть с точностью до 0,05% можно считать, что μ=m и электрон движется в поле неподвижного ядра [1-4].
Для трёхчастичной задачи уже нет точного решения, а есть численные решения уравнения Фадеева [5], в основном для задачи трёхчастного рассеяния с обобщениями на рассеяние большего числа частиц.
Поэтому многочастичная задача решается приближенно. Для атомов и молекул приближённое разделение движения электронов и ядер основывается на указанном выше соотношении их масс,
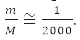
Для решаемой в этом случае многоэлектронной задачи в поле неподвижных ядер атомов молекулы тоже развиты приближённые методы: от конфигурационного взаимодействия до разных методов самосогласованного поля, основанные на применении вариационного метода [4].
Впервые разделение электронного и ядерного движений было проведено в работе Борна и Оппенгеймера [6].
Если отвлечься от поступательного движения молекулы, как целого, то по порядку их значений можно выделить три вида движения – движение электронов в поле ядер, колебания ядер относительно центра масс молекулы, которые движутся медленно по сравнению с электронами в усреднённом их поле, и вращений молекулы вокруг осей, приходящий через центр масс. При этом, Eэл.мол ≫ Eэл.мол ≫ Eэл.мол, и полная энергия молекулы: E = Eэл. + Eкол. + Eвр. В этом приближении ψ = ψэл. + ψкол. + ψвр.. Каждому фиксированному положению ядер отвечает определённая энергия Eэл.({R}). В этом смысле электронная энергия, как функция межядерных расстояний, играет для самих ядер роль потенциальной энергии. Для устойчивых многоатомных молекул получен простой критерий применимости приближений Борна-Оппенгеймера:
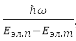
где ω – наибольшая из циклических частот нормальных колебаний ядер вблизи точек равновесия, Eэл.п и Eэл.т – энергии соседних электронных состояний.
5. Теорема Яна-Теллера
В 1937 году Ян и Теллер доказали теорему, ограничивающую возможные конфигурации для ядер атомов у нелинейных молекулярных систем. Её доказательство основано на теории возмущений для вырожденных электронных состояний симметричной молекулы относительно смещений атомов молекулы при нормальных её колебаниях, класифицированных по неприводимым представлениям группы симметрии молекулы. Для всех молекул, кроме линейных, её доказательство основано на наличии в разложении квадрата неприводимого представления её вырожденного электронного состояния любого неприводимого представления из возможных для нормальных колебаний молекулы (см. стр. 209-226 в [7]).
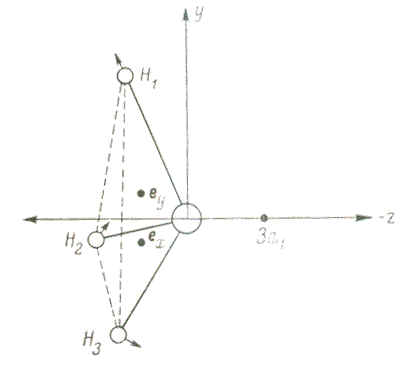
Рисунок 2 — Ян-теллеровские сдвиги в молекуле BH3
В 1959 году Клинтон и Райс опираясь на теорему Гельмана-Фейнмана дали новое обоснование для теоремы
Яна-Теллера, физическая суть которого связана с силовым воздействием заряда облака электронов
в
основном
вырожденном соотношении молекулы (определяемого их плотностью) на ядро каждого атома. На примере молекул
симметрии D3h и D4h они показали возможность стабилизации для них
несимметричной геометрии, которую могут
вызвать колебания ядер с симметрией B1g и B2g (см. стр. 379-389 в [7]).
Стоит отметить, что линейное уравнение Шрёдингера при симметричном расположении ядер молекулы имеет решение,
принадлежащее неприводимому представлению группы симметрии такой молекулы. Если её основное электронное
состояние вырождено, то при реализации одной из компонент состояния его электронная плотность оказывается не
симметричной и сила их кулоновского взаимодействия с медленными ядрами
, в указанных Яном и Теллером
случаях, может привести к понижению симметрии молекулы. Вследствие линейности уравнения (7) это отразится и
на его решении для волновой функции электронов, симметрия которой тоже понизится и, в итоге, вырождение
основного состояния снимется.
6. Приближение самосогласованного поля
Волновая функция для многоэлектронной задачи определяется из решения уравнения Шредингера (7) в приближении Борна-Оппенгеймера при неподвижных ядрах. Спиновые взаимодействия обычно учитываются по теории возмущений.
Невозможность точного решения уравнения (7) привели к развитию приближенных методов, основанных на минимизации среднего значения Гамильтониана, вычисленного для определённой пробной функции. Когда она представлена в виде разложения по детерминантам из спинорбиталей, взятых из определённого базиса, имеем метод конфигурационного взаимодействия (КВ) [8,9]. Требование антисимметрии волновой функции, как сказано выше, следует из принципа Паули. Методы КВ основанные на базисе собственных функций одноэлектронного Гамильтониана позволяют классифицировать энергетические уровни, но не являются практически удобными для расчётов.
Более эффективным является метод самосогласованного поля Хартри-Фока. Метод Хартри не учитывал принцип Паули. А Фок исправил его, записав вместо произведения орбиталей детерминант из них. Получаемые из вариационного принципа для молекулярных орбиталей такой функции уравнения существенно нелинейные. Для них получена и орбитальная запись [1-4] и матричная форма [10]. В последнем случае функционал энергии в спин орбитальном виде [11] записывается так:
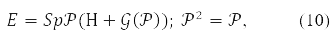
где любая из матриц P,H,𝒢(P), в (9) разложима по матрицам Паули, действующим в спиновом пространстве
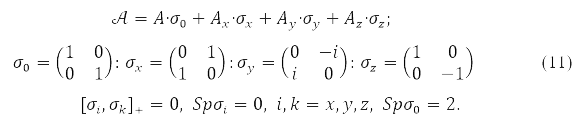
Функционал (9), как частные случаи, включает: и приближение разные орбитали для разных спинов (РОРС), так называемый неограниченный метод Хартри-Фока (НХР), и приближение с двух кратным заполнением орбиталей замкнутой оболочки – ограниченный метод Хартри-Фока (ОХФ). В НХФ методе определённое значение имеет только проекция спина, а в ОХФ методе и полный спин электронов, и его проекция.
Вместо одноэлектронной плотности в задачах с применением 1-й и 2-й вариации функционала энергии, δE и δ2E, удобно применять инволютивную матрицу:
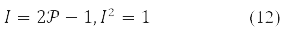
С ней функционал (9) приобретает вид:
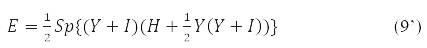
и условие стационарности
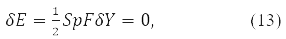
где
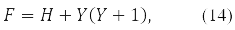
даёт уравнение:
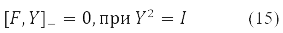
Дальнейшее варьирование энергии
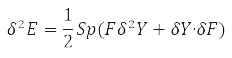
c учетом про свойств степеней Y-матрицы окончательно даёт значение:
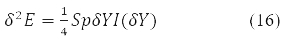
Где δY = D – матрица вариации инволютивной матрицы, подчиннённой условию
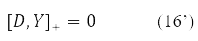
Вариация D преобразуется в (15) в новую эрмитовую матрицу I(D) согласно правилу [11].
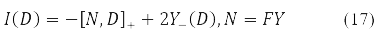
Компактный спин орбитальный вид уравнений Хартри-Фока (14) и второй вариации энергии (15)-(16) становятся возможным благодаря матричной [10] записи и функционала энергии, и 1-й и 2-й его вариации.
В случае δ2E ≤ 0 получаем условие нестабильности решения уравнений (14) для стационарного состояния. Этой ситуации отвечает не положительные собственные значения оператора стабильности (16)
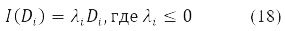
Из формы записи уравнений (14)-(17) можно извлечь не только разные варианты метода Хартри-Фока, но и рассмотреть его нестабильности относительно разного вида матриц Д, как без переворота спина так и с переворотом спина. В работе [12], например, доказана универсальная нестабильность ограниченного метода Хартри-Фока (ОХФ) относительно вариации орбиталей (и соответственно матрицы Д) с переворотом спина для состояния с произвольными полным спином.
Разные методы Хартри-Фока получил при определенных требованиях на разложимость (10) плотности У по матрицам Паули. Так, ОХФ методу с замкнутой оболочкой отвечает Y = Y0δ0 при Y2 = 1, уравнения самосогласованного поля
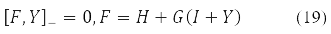
где
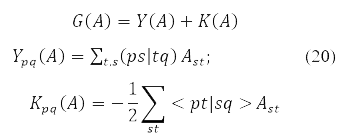
и функционал энергии
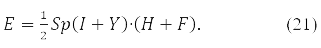
В (19) <qt|qs> – интеграл 2-х частичного кулоновского взаимодействия электронов
на
орбитах xp,xt,xq,xs.
Список источников
- Ландау Л.Д. Теоретическая физика. Т. 3: Квантовая механика / Л.Д. Ландау, Е.М. Лифшиц. – 5-е изд. – М.: Физматлит, 2002. – 767 с.
- Мессиа А. Квантовая механика. Т.1 / А. Мессиа. – М.: Наука, 1978. – 478 с.
- Мессиа А. Квантовая механика. Т.2 / А. Мессиа. – М.: Наука, 1979. – 584 с.
- Соколов И.М. Квантовая химия: учеб. пособие / И.М. Соколов. – СПб.: Изд-во Политехн. ун-та, 2010. – 122 с.
- Шмид Э., Цигельман Х. Проблема трёх тел в квантовой механике, монография, перев. с англ. – М.: Наука, 1979, – 272 с.
- Born M., Oppenheimer J.R., Ann. Physik, 1927, V.84, – p. 45
- Нокс Р. и Голд А. Симметрия в твёрдом теле. – М.: Наука, 1970. – 424 с.
- Foresman J. B., Нead-Gordon М., Pople J. A., Frisch М. J. J. Phys. Chem., 1992, v. 96, р. 135.
- Head-Gordon M., Rico R.J., Oumi M., Lee T.J. – Chem. Phys. Jett., 1994, V.219, p. 21
- Местечкин М. М. Метод матрицы плотности в теории молекул. – Киев: «Наукова думка», 1977. – 352 с.
- Местечкин М.М. Нестабильность уравнений Хартри-Фока и устойчивость молекул. – Киев: «Наукова думка», 1986. – 176 с.
- Mestechkin M.M., Klimko G.T., Whyman G.E. On the universal instability of the open-shell Restricted Hartry-Fock method. // Chem. Phys. Lett. – 1985. – V. 115, № 6. – 531 – 534.
- Roothaan C. C. J. Self-Consistent Field Theory for Open Shells of Electronic Systems. – Rev. Mod. Phys., 1960. V. 32, P. 179 – 186.
