
| RUS | | ENG | | UKR | | CATALOG | | MY WORK |
Грузовой (скиповый) подъем на горном предприятии является одним из важнейших основных технологических объектов, от эффективной и производительной работы которого зависит выполнение шахтой плановых нормативов по добыче горной массы, ритмичной работы добычных участков, производительность рабочих коллективов и оборудования.
Применительно к скиповому подъему это достигается решением задач:
Цель работы - решение вышеуказанных задач путем исследования основных временных показателей, характеризующих процесс подъема – скорости движения, времени движения (спуска и подъема), времени технологических пауз между циклами.
Шахтный грузовой подъем (ШГП) характеризуется циклическим режимом работы с широким изменением концевой нагрузки по циклам, а также является установкой программного управления. Вид и количество периодов расчетной тахограммы определяется технологическими свойствами подъема. На рисунке 1 приведена шестипериодная диаграмма скорости ШГП.
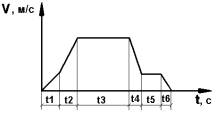
Рисунок 1 - Шестипериодная диаграмма скорости ШГП
На тахограмме приняты следующие временные периоды:
· t1 – период ускоренного движения.
· t2 – период ускоренного движения.
· t3 – период равномерного хода.
· t4 – период замедления.
· t5 – период равномерного хода.
· t6 – период стопорения.
Когда исследование на реальном объекте невозможно, эффективным и целесообразным методом исследования является метод моделирования.
Несмотря на развитую теорию аналитических методов, качественный и количественный анализ сложных систем аналитическими моделями иногда встречает значительные трудности. В этих случаях используют имитационное моделирование, в основе которого лежит особый численный метод (Монте-Карло), с помощью которого имитируются элементарные явления, составляющие исследуемый процесс.
Сущность метода в том, что процесс имитируется с помощью арифметических и логических операций в последовательности элементарных актов, характерных процессу.
Метод моделирования непрерывных величин - метод обратных функций, основан на соотношении функции распределения F(x) непрерывной случайной величины х, плотности распределения вероятности f(x) и равномерно распределенных (0;1) случайных чисел x и описывается следующим образом, рис. 2:
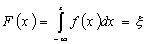 (1)
(1)
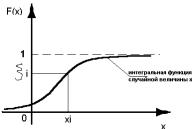
Рисунок 2 - Метод обратных функций
Обработка одномерных случайных величин производится в следующем порядке:
· построение вариационного ряда выборки одномерной случайной величины;
· определение ориентировочного значения количества интервалов группирования;
· определяются основные статистические характеристики выборки: математическое ожидание; дисперсия; стандарт.
Для нормального закона распределения плотность вероятности:
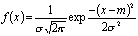 (3)
(3)
Для логнормального закона распределения плотность вероятности:
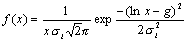 (4)
(4)
При моделировании объекта для получения приемлемой точности определяется необходимое число реализаций исследуемых параметров объекта:
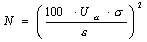 (5)
(5)
где Ua - квантиль нормального распределения, Ua=1,96:
e - необходимая точность, e=10%.
Т.к. время движения и время технологической паузы являются случайными величинами, то по методу обратных функций:
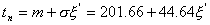 (6)
(6)
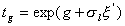 (7)
(7)
Модель движения ШГП:
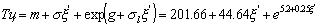
Погрешность измерений (по мат. ожиданию) составляет:
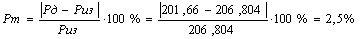
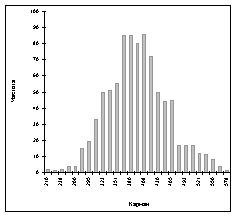
Если провести усреднение гистограммы, представленной на рисунке, то можно выделить шесть отрезков, соответствующих теоретической шестипериодной диаграмме скорости. Т.о. результаты моделирования адекватны реальному объекту.
1. Потапов В.Д., Яризов А.Д. Имитационное моделирование производственных процессов в горной промышленности. – М. : «Высшая школа», 1981 – 190 с.
2. Правила технической эксплуатации угольных шахт и рудников. – М.: Недра, 1976 – 303 с.
3. Бурчаков А.С., Ливенцев В.В. Математическое моделирование в горной промышленности. – М.: «Высшая школа», 1967 – 215 с.