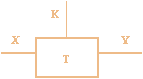
Рис. 1. Двунаправленный ключ
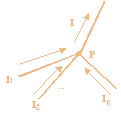
Рис. 2. Коннектор
В статье излагается унифицированный подход к моделированию сетевых структур с циркулирующими в них сигналами различной физической природы, значения которых образуют дискретное конечное множество. Предлагается универсальное представление моделирования сетевых структур итерационным процессом вычислений решения системы булевых уравнений вида X = MÅF(X). Здесь X - многозначный вектор значений сигналов в узлах схемы, M - операция свертки или выбора результирующего сигнала из множества воздействующих сигналов в узле, а F - функция преобразования, определяемая системой булевых уравнений. Рассматривается применение этого представления к моделированию логических вентильных сетей, дискретных МОП-схем и головного мозга, как совокупности нелинейных осцилляторов. Возможность параллельных вычислений для булевых выражений позволяет эффективно реализовывать предложенные алгоритмы.
В сущности, предлагается подход, основанный на идеях "наивной" физики и использующий различного рода дискретизации физических сигналов. Считаются справедливыми следующие положения:
|
|
|
|
Рис. 1. Двунаправленный ключ |
Рис. 2. Коннектор |