Многие виды движений животных содержат в своей основе циклические процессы. Так, при локомоции - активном перемещении животною в пространстве - можно наблюдать повторяющуюся смену положений конечностей (ходьба, бег четвероногих) или ритмические изгибания тела (плавание у рыб). Экспериментальные исследования пространственной и временной организации локомоторного паттерна служат основой осцилляторных моделей нейронных сетей. Эти модели объясняют некоторые особенности координации движений и переходов от одного типа движения к другому. При этом основное внимание уделяется моделированию центрального генератора паттернов. Центральным генератором паттернов называют нейронную сеть, которая способна демонстрировать различные наборы динамических паттернов активности, соответствующих тем или иным типам движений. Здесь мы ограничимся рассмотрением моделей ОНС, относящихся к ходьбе четвероногих и плаванию некоторых видов рыб.
Для животных характерно наличие различных типов походки, аллюров (см. например, книгу В.Б. Суханова [71]). Они различаются по фазовым отношениям между движениями конечностей. При росте скорости движения происходят изменение этих соотношений (плавное или скачкообразное), т.е. животное меняет тип походки. Для многих четвероногих существует естественное упорядочение аллюров по частоте движения конечностей: шаг, рысь, квазигалоп, галоп или иноходь. При движении с пороговой скоростью возможны спонтанные переходы от одного аллюра к другому. Эксперименты, демонстрирующие переходы от одного типа движений к другому при изменении скорости движения, описаны во многих работах (см., например, [1,5,61,124]). При экспериментальных исследованиях скоординированных движений одноименных пальцев на разных руках Дж. Келсо, Дж. Шольц, Г. Шенер [61,101] показали, что переход от противофазных движений к синфазным имеет сходство с фазовым переходом. Измерения демонстрируют аномальное замедление времени и рост флуктуации вбвизи точки перехода.
В качестве модели, объясняющей
экспериментальные факты, часто
рассматривается система связанных фазовых
осцилляторов типа (2.3), где движению каждой
конечности ставится в соответствие
уравнение динамики фазы. В данном случае
учитываются только четыре парных
взаимодействия: между передними, задними,
левыми и правыми конечностями. Раскладывая
в ряд Фурье 2p-периодические
нечетные функции взаимодействия (нечетность
- следствие определенных симметрий
рассматриваемых аллюров) и ограничиваясь
при этом членами второго порядка, Г. Шенер и
др. [99] получают систему уравнений для фаз qij
(первый индекс iÎ{l,r}, т.е.
относится к левой или правой конечности,
второй - jÎ{f,h} - к
передней или задней конечности). Наличию
инвариантности к сдвигу по времени
позволяет считать, что фазовая динамика
зависит только от относительных фаз, и
выписать уравнения для трех фаз
относительно четвертой fij=qij-qrf:
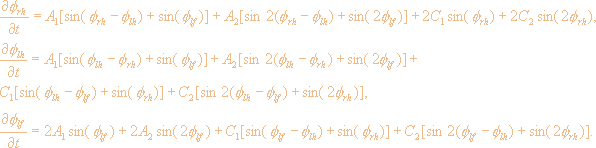 |
(5.1) |
Заметим, что основным аллюрам
соответствуют следующие значения вектора (flf,
frf, flh,
frh): (0,0,0,0) - прыжок; (0,p,p,0)
- рысь; (0,0,p,p)
- галоп; (0,p,0,p)
- иноходь; (0,0,p-j,p-j)
и (0,0,-p+j,-p+j)
- прямой и обратный квази-галоп; (p,0,j,-p+j)
и (p,0,j,p-j)
- прямой и обратный шаг, где jÎ(0;p/2).
Подстановкой можно убедиться, что рысь,
галоп, иноходь и прыжок являются
стационарными решениями уравнений (5.1).
Легко найти еще два стационарных решения:
flf = 0; f0rh = +arccos(-C1/2C2); f0lh = f0rh |
(5.2) |
flf = p; f0rh = +arccos(-C1/2C2); f0lh = f0rh -p |
(5.3) |
Решения (5.2) соответствуют прямому и обратному квази-галопу, а (5.3) - движению шагом. Изменяя параметры C1 и C2, можно получить слияние прямого и обратного квази-галопов в галоп (если C1/2C2 ®+1) или в прыжок (при C1/2 C2 ®-1). Аналогично, движения прямым и обратным шагом переходят в рысь при C1/2C2 ®+1 и в иноходь при C1/2 C2 ®-1. При |C1/2 C2| > 1 только четыре основных паттерна остаются решениями.
Исследование устойчивости стационарных состояний в работе [99] проводится стандартным образом. Кроме того, в пространстве параметров А1,А2,С1,С2 авторы наблюдают фазовые переходы различных типов, возникающие при пересечении границ между областями, соответствующими различным режимам. При таких фазовых переходах может происходить потеря устойчивости как мягко, с плавным изменением стационарных значений, так и жестко, с резким изменением.
В работах X. Юаса, М. Ито [127] и Г. Шенера, Дж. Келсо [100] при моделировании различных типов движений (движения пальцев, плавание рыб, походки) рассматриваются градиентные системы. Минимальные значения потенциальной функции соответствуют различным паттернам движения. Изменение формы потенциальной функции приводит к переходам от одного паттерна к другому.
Целый ряд интересных экспериментальных данных был получен при изучении плавания рыб. Особый интерес представляют исследования, выполненные на миноге, которая плавает, ритмически изгибая тело. Управление плаванием осуществляется спинным мозгом, вдоль которого расположены вентральные корешки, передающие сигналы мышцам.
В основу моделирования плавания миноги были положены следующие основные факты, содержащиеся в работах П. Уоллена, Т. Уильямса [117] и Т. Уильямса и др. [119]:
Для того чтобы объяснить описанные факты, Р. Рэнд, А. Коэн и др. [25,90] и Н. Копель и др. [66,68,119] рассматривают спинной мозг как цепочку связанных осцилляторов, каждый из которых описывает активность вентрального корешка. Моделирование ведется на основе фазовых осцилляторов.
В работах [25,90] исследуются уравнения
динамики фаз типа (2.3) с локальными связями:
| (5.4) |
где qi - фаза, (wi - собственная частота i-го осциллятора; А - величина связи соседних осцилляторов). Переходя к уравнениям для разностей фаз, находят стационарные решения этой системы. Существование таких решений означает, что в системе установится режим колебаний, когда все осцилляторы работают с одной и той же частотой, равной среднему арифметическому собственных частот осцилляторов, и разность фаз любых двух соседних осцилляторов остается постоянной. Таким образом, можно получить бегущую волну на цепочке осцилляторов. Эта же модель распространяется на случай цепочки со связями второго порядка и на случай двух цепочек осцилляторов с локальными связями между цепочками [25,90].
В работах [66,68,119] обсуждается модель центрального генератора паттернов плавания миноги. Существование синхронизованных по фазе колебаний позволяет построить модель плавания, причем удается объяснить как "прямое", так и "обратное" плавание. При наличии небольшого градиента собственных частот волна активности с постоянной скоростью может распространяться вдоль цепочки осцилляторов от одного конца к другому (см. уравнение (2.16)). При этом все осцилляторы работают с одной и той же частотой и постоянной разностью фаз. При однородных связях "лидирующий" осциллятор, являющийся источником волн, будет располагаться в середине цепочки, и с помощью небольшого возмущения может быть смещен к хвостовому концу, тем самым в модели будет реализовываться режим "плавание назад", который наблюдается экспериментально.