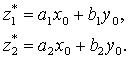Алгоритм Мамдани

    Предположим, что базу знаний образуют два нечётких правила:
     П1: если х есть А1 и y есть В1, то z есть С1,
     П2: если х есть А2 и y есть В2, то z есть С2,
где х и у - имена входных переменных, z - имя переменной вывода, А1, А2, В1, В2, С1, С2 - некоторые заданные функции принадлежности, при этом чёткое знание z0 необходимо определить на основании приведённой информации и чётких знаний x0, y0.
     Данный алгоритм математически может быть описан следующим образом.
    1. Нечёткость: находятся степени истинности для предпосылок каждого правила: А1(х0), А2(х0), В1(х0), В2(х0).
    2. Нечёткий вывод: находятся уровни отсечения для предпосылок каждого из правил (с использованием операции минимума):
    
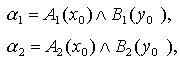
    где через "^" обозначена операция логического минимума.
    Затем находят усечённые функции принадлежности:
    
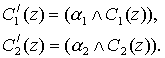
    3. Композиция: с использованием операции max (обозначенной как "v") производится объединение найденных усеченных функций, что приводит к получению итогового нечёткого подмножества для переменной выхода с функцией принадлежности
    
    4. Приведение к чёткости (для нахождения z0) производится, например, центроидным методом (как центр тяжести для кривой функции принадлежности):
    

Алгоритм Сугэно

     Сугэно и Такаги использовали набор правил в следующей форме (как и раньше, приводим пример двух правил):
     П1: если х есть А1 и y есть В1, то z1=a1x+b1y,
     П2: если х есть А2 и y есть В2, то z2=a2x+b2y.
    1. Первый этап - как алгоритме Мамдани.
    2. На втором этапе находятся уровни отсечения для предпосылок каждого правила - как в алгоритме Мамдани и индивидуальные выходы правил по формулам:
    
    3. На третьем этапе определяется чёткое значение переменной вывода: