|
[ Комплексная автоматизация для дегазации и утилизации метана. ] [ Аппаратно-програмный комплекс автоматизации контроля состояния рудничной атмосферы. ] [ MATLAB для DSP. Применение многоскоростных фильтров в задачах узкополосной фильтрации. ] |
MATLAB для DSP. Применение многоскоростных фильтров в задачах узкополосной фильтрации. В. Анохин, А. Ланнэ. Chip-News. 2000. № 2. С. 4–7. |
Многоскоростные фильтры и банки фильтров (фильтры и банки фильтров с многочастотной дискретизацией) определили самостоятельное направление в теории и практике цифровой обработки сигналов (ЦОС). В этой связи достаточно упомянуть квадратурно-зеркальные фильтры — новый класс многополосных фильтров, банки многоскоростных фильтров для реализации вейвлет-преобразований, полифазные фильтры. Многоскоростная фильтрация нашла широкое практическое применение в задачах компрессии речи, звука и изображений, построения эффективных систем фильтрации, очистки сигнала от помех, оптимизации вычислительных ресурсов при реализации алгоритмов ЦОС. Для решения задач анализа (моделирования) и синтеза (проектирования)
систем с многочастотной дискретизацией пакет MATLAB предоставляет широкие
возможности. В рамках проекта "MATLAB для DSP" рассмотрим частную, но
практически важную задачу проектирования и моделирования узкополосного
фильтра. Для этих целей, как это и оговорено в проекте, используются два
наиболее дружественных для пользователя инструмента MATLAB - Simulink и
GUI. Основные соотношения теории многочастотной дискретизации. Основы теории многоскоростной фильтрации (многоскоростной обработки сигналов) и описание приложений можно найти в [1-4]. В качестве базовых при многочастотной дискретизации используются:
Таким образом, частота дискретизации fs сигнала x(n) связана с частотой дискретизации f's соотношением Mf's = f's , или соотношением периодов дискретизации T' = MT. Частоты дискретизации сигналов x(n) (частота fs ) и yl(n) (частота fs ) при интерполяции связаны соотношениями f's = Lfs или T = LT'. Пример децимации сигнала x(n) при M = 2: отсчёты сигнала до (а) и после (б) децимации.
Пример интерполяции сигнала x(n) при L = 2: отсчёты сигнала до (а) и после (б) интерполяции
При децимации и интерполяции сигнала происходит деформация
спектров.
где z = ejw , а и, следовательно,
где нормированная частота w = wT', а T' - период дискретизации после децимации. Он будет в M раз больше, так что в шкале ненормированных частот получим
Учитывая, что T' = MT , можно записать окончательное соотношение между спектрами децимированного сигнала YD(ejw) и исходного X(ejw):
Для интерполяции YI(z) = X(zL) или
YI(ejw) = X(ejwL) или
YI(ejw) = X(ejwL).
Полифазное разбиение и полифазные фильтры. Передаточная функция нерекурсивного (КИХ - конечной импульсной характеристики) фильтра
может быть представлено суммой
Смысл многочленов E0 и E1 понятен из
контекста.Если E0 и E1 рассматривать как
передаточные функции КИХ-фильтров, то нетрудно заметить, что базовым
элементом задержки таких фильтров является z-2, обеспечивающий
задержку на два такта. Следовательно, фильтры E0 и
E1 могут работать на частоте дискретизации, в два раза меньшей
исходной. Если использовать разложения по степеням z-3 или
z-4 и так далее, то можно получить блоки фильтров,
работающие на ещё более низких частотах дискретизации. Итоговая схема
фильтра, когда
Рассмотренное разбиение называется полифазным, а реализующие его схемы - полифазными фильтрами.В качестве примера, иллюстрирующего построение полифазного фильтра и использование замечательных тождеств, покажем, как можно эффективно реализовать КИХ-фильтр дециматор.
В схеме рис. 8 для вычисления каждого отсчёта необходимо выполнить N+1 умножений и N сложений. В то же время, за счёт децимации (M = 2) половину результатов отсчётов мы отбрасываем и, следовательно, используем ресурсы вычислителя неэффективно.Построим фильтр на основе полифазного разбиения (полифазный фильтр, рис. 7) и воспользуемся замечательным тождеством (рис. 5). Последовательность преобразований при этом показана на рис. 9.
В результате фильтры E0(z2) и E1(z2), работающие на частоте fs, заменяются фильтрами E0(z) и E1(z), работающими на частоте fs/2. Таким образом мы получим двукратную эконом ию в скорости вычислений. При коэффициенте децимации M применение полифазных фильтров позволяет получить экономию в M раз. Аналогичные результаты получаются и при полифазном построении фильтров интерполяторов [1,2]. Таким образом, полифазные реализации в совокупности с рациональными преобразованиями схем фильтров позволяют строить эффективные вычислители в задачах ЦОС. Расчёт узкополосного низкочастотного фильтра. В процессе цифровой обработки сигналов нередко возникает задача
фильтрации сигнала в очень узком частотном диапазоне. Примером такой
задачи может служить ситуация, когда сигнал содержит несколько
составляющих на близких частотах, и требуется выделить одну из них. Для
этого необходимо спроектировать цифровой фильтр с очень узкими
относительными полосами пропускания и перехода. В зависимости от
расположения составляющих сигнала, это может быть фильтр нижних, верхних
частот, полосовой или заграждающий фильтр. Прямое проектирование таких
устройств часто приводит к фильтрам очень высоких порядков, практическая
реализация которых либо нерациональна, либо невозможна. u(n) = sin(2πf1nT) + sin(2πf2nT) + e(n) , где f1 = 90 Гц и f2 = 105 Гц - частоты составляющих; T = 1/fs = 1/8000 с - период дискретизации; fs = 8000 Гц - частота дискретизации; e(n) - гауссовский шум с нулевым средним и дисперсией σ2 = 0,1. Требуется выделить синусоидальную составляющую с частотой f1. Для этого необходимо построить фильтр нижних частот с граничными значениями частот полосы пропускания fpb и полосы задерживания fsb, удовлетворяющими условию f1 < fpb< fsb < f2 . Поскольку частота Найквиста fN = fs/2 = 4000 Гц, для нормализованных значений fpb = fpb/fN и fsb = fsb/fN это условие будет выглядеть так :
Следовательно, переходная полоса Δf амплитудно-частотной характеристики
фильтра (АЧХ) не должна превышать величину Δf < 0,02625 – 0,0225 =
0,00375. Эти требования схематически показаны на рис. 10.
|


 Рис 3.
Рис 3.  Рис 4.
Рис 4. 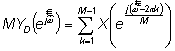
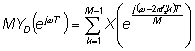
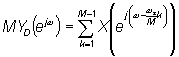

 Рис 8.
Рис 8.  Рис. 9
Рис. 9