




Геометрическое моделирование сплошных тел
Алексей Игнатенкоignatenko@graphics.cs.msu.su
Источник http://graphics.cs.msu.su/ru/library/3d/solid_modelling/index.html
- Введение
- 1 Моделирование путем разложения пространства на элементы
- 2 Пространственная геометрия (CSG)
- 3 Boundary representation (B-rep) (граничное, поверхностное представление)
- 4 Литература
Введение
Задача геометрического моделирования сплошных тел является
важной областью машинной графики.
Поскольку данные о физических
объектах реального мира не могут быть целиком введены в компьютер,
необходимо априори ограничить объем информации об объекте в рамках
интересующего нас вопроса. Например, задача рендеринга объекта с
затенением поднимает такие проблемы как:
- Какие части объекта видимы?
- Какой цвет должен быть присвоен каждому элементу объекта?
И если будет выбрано подходящее представление
геометрической модели объекта для данной проблемы, она будет решена
эффективно, и наоборот.
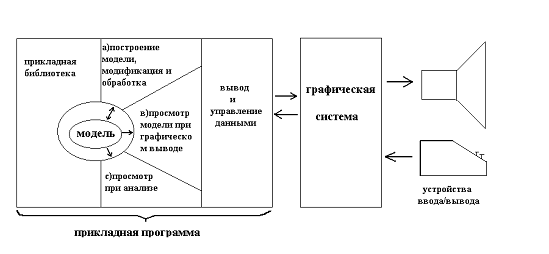
Рисунок 1 Основные операции над геометрическими моделями
Рассмотрим основные классы
представлений сплошных объектов для решения наиболее общих
задач.
1 Моделирование путем разложения пространства на элементы
Моделирование путем разложения описывает сплошные тела через
комбинацию некоторых сплошных блоков, соединенных вместе тем или
иным образом. Тип базовых объектов определяет различные методы
моделирования этим способом.
1.1 Воксельное представление
Разобьем интересующую нас область пространства
E3 на набор кубов (вокселей). Таким образом, мы можем
сопоставить ей трехмерный массив cijk .Элемент массива
равен 1, если куб cijk представляет собой область,
занятую неким объектом, и 0 в противном случае. В некоторых случаях
удобно применять некоторые промежуточные значение, задавая тем самым
плотность в данной точке пространства. Как легко видеть (см.
рисунок), мы получаем трехмерную модель интересующего нас объекта.
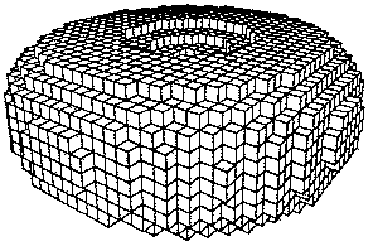
Рисунок 2 Воксельное представление
Некоторые характеристики такого представления:
- Такое представление дает только приближение реального объекта. Поверхности, не параллельные осям координат, представляются приблизительно. Качество приближения зависит от относительного размера вокселей.
- Требует больших размеров памяти для хранения, и эти требования резко возрастают при увеличении разрешения (растет как куб от разрешения).
- С таким представлением хорошо работают в основном пространственные алгоритмы, такие как вычисление объема объекта, нахождение центра масс и т.д.
1.2 Октарные и бинарные деревья
Одним из недостатков воксельной модели является большой объем
памяти, требуемой для хранения информации о разбиении пространства.
Если мы будем хранить информацию только о блоках, относящихся к
объекту, мы получим, что число элементов, требуемых для
представления объекта, пропорционально площади его поверхности, т.е.
пропорционально квадрату разрешения, а не кубу, как в предыдущем
случае.
1.2.1 Октарные деревья
Октарные деревья представляют собой рекурсивное разбиение
пространства на восемь октант, которое представляется деревом (см.
рисунок (а)). Обычно октарное дерево располагаются вокруг начала его
локальной системы координат, так что октанты первого уровня
совпадают с октантами системы координат.

Рисунок 3 Пример октарного дерева.
Каждая ветвь дерева состоит из кода и восьми указателей
на восемь потомков, пронумерованных от 0 до 7. Если код = "черный",
часть пространства, представляемая этой ветвью является заполненной
и все указатели нулевые, т.е это лист. Аналогично, если код =
"белый", часть пространства пустая и это опять лист. Код = "серый"
соответствует случаю, когда область пространства частично пуста и
частично заполнена. В этом случае 8 ссылок указывают на подразбиение
данной области. Например, на рисунке объект (в) представляется
деревом (с)
Примечание: Если рассматривается плоский
случай (2D), то мы получаем квадро-деревья. В этом случае плоскость
рекурсивно разбивается на занумерованные квадранты.
Графический вывод
Очень важным достоинством октарных деревьев является то, что
они хранят информацию в упорядоченном виде. Это дает нам возможность
разработать простые алгоритмы рендеринга объектов, представляемых в
таком виде. Например, если точка наблюдения расположена в октанте x,
y, z>0, упорядочение дерева 4, 0, 5, 1, 6, 2, 7, 3 будет давать
корректные результаты (при условии вывода back-to-front)
Линейное представление
Напомним, что октанты дерева пронумерованы от 0 до 7. Эти числа
могут быть использованы для конструирования адреса каждой ветви
дерева, кроме корня. Адрес ветви уровня i есть последовательность i
чисел от 0 до 7 – путь от корня к этой ветви. Также можно включить
специальный символ X для обозначения того, что в последовательности
чисел меньше, чем максимальное разрешение. При таком подходе
линейная запись дерева есть просто сортированный массив адресов
ветвей с кодом "черный". Например, дерево на рисунке кодируется
следующей последовательностью: {03,1X,51,53}
Другой подход к
линейному представлению дерева базируется на обходе дерева в
фиксированном порядке, например, слева направо, сверху вниз.
Кодирование использует трехсимвольный алгоритм "B","W" и "("
(обозначают соответственно "черную" ветвь, "белую" ветвь и
нелистовую ветвь). Дерево на рисунке кодируется в этом случае
следующей строкой:
1.2.2 Бинарные деревья
Как альтернатива октарному делению пространства также возможно
бинарное деление. Это представление очень похоже на предыдущее. Но
здесь производится деление пространства пополам, а не на восемь
частей. Деление производится последовательно в направлении осей x,y
и z.
По сравнению с октарными деревьями, бинарные требуют
немного меньше памяти для хранения. Также возможна линейная запись
таких деревьев по аналогии с октарными. Например, для дерева,
изображенного на рисунке, линейная запись будет такой:

Рисунок 4 Бинарное дерево
Некоторые характеристики деревьев:
- Так же как воксельное представление, октарные и бинарные деревья дают только приблизительное представление объекта, и модель дает хорошие результаты только на ограниченном классе объектов.
- Поддерживает эффективное выполнение булевых операций над деревьями ( пересечение, объединение), геометрические операции (такие как перемещение, поворот, изменение размера)
- Объем памяти, требуемый для хранения деревьев, пропорционален площади поверхности объекта.
2 Пространственная геометрия (CSG)
В пространственной
геометрии объект задается набором примитивов и операций над ними.
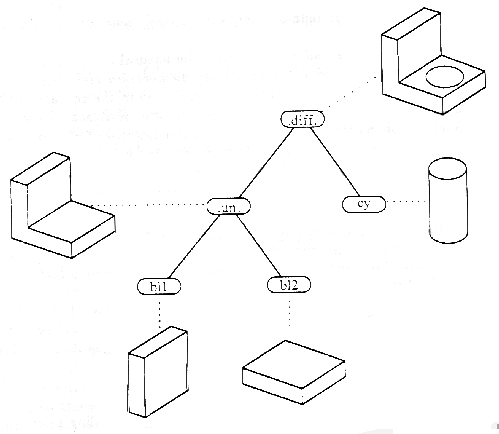
Рисунок 5 Дерево пространственной геометрии
Примитивы являются "строительными блоками" нашего объекта. Под
операциями понимаются булевы операции над примитивами, а также
геометрические преобразования, такие как передвижение, поворот,
изменение размеров.
Можно говорить о дереве пространственной
геометрии. Листьями дерева являются геометрические примитивы, каждой
ветви сопоставляется операция. Вершиной дерева является искомый
геометрический объект. Поскольку каждый примитив может быть
использован несколько раз, дерево превращается в направленный
ациклический граф.
3 Boundary representation (B-rep) (граничное, поверхностное представление)
В отличие от ранее описанных
моделей, поверхностное представление определяет сплошное тело неявно
путем описание ограничивающей его поверхности.

Рисунок 6 Основные составляющие граничной модели
Поскольку глобальная параметризация поверхности объекта
произвольной формы обычно является трудновыполнимой задачей,
поверхность приближается набором граней (face). Обычно
разбиение выполняется таким образом, чтобы каждая грань имела
компактное математическое представление.
Границы граней
представляется ребрами (edge). Так - же как и грани, ребра
выбираются таким образом, чтобы иметь компактное математическое
описание. Часть кривой, формирующей ребро, заканчивается
вершинами (vertex).
Поверхностная модель, которая имеет
только плоские грани, называется полигональной моделью.
Рассмотрим возможные варианты задания полигональной модели.
3.1 Явное представление.
В этом случае каждая грань есть полигон, состоящий из
последовательности координат вершин. Объект состоит из набора
граней.
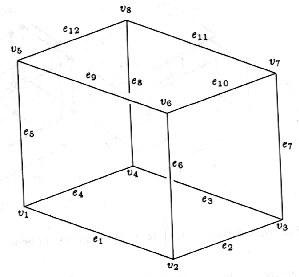
Рисунок 7 Пример
Недостатки такого представления в том, что, во-первых,
взаимоотношения граней заданы неявно, а во-вторых, координаты каждой
вершины появляются столько раз, сколько граней имеют эту
вершину.
3.2 Список вершин
Повторяемость координат вершин можно обойти путем выделения
координат вершин в отдельную структуру. В этом случае с гранями
ассоциируются не координаты вершин, как в предыдущем случае, а
индексы в массиве координат вершин. В нашем примере (см. рисунок )
будем иметь:
|
Вершины |
Координаты |
Грани |
Вершины |
|
v1 |
x1 y1 z1 |
f1 |
v1 v2 v3 v4 |
|
v2 |
x2 y2 z2 |
f2 |
v6 v2 v1 v5 |
|
v3 |
x3 y3 z3 |
f3 |
v7 v3 v2 v6 |
|
v4 |
x4 y4 z4 |
f4 |
v8 v4 v3 v7 |
|
v5 |
x5 y5 z5 |
f5 |
v5 v1 v4 v8 |
|
v6 |
x6 y6 z6 |
f6 |
v8 v7 v6 v5 |
|
v7 |
x7 y7 z7 |
||
|
v8 |
x8 y8 z8 |
Заметим, что список вершин каждой грани упорядочен по
часовой стрелке, как если смотреть снаружи куба. Такое представление
полезно во многих алгоритмах, таких как удаление невидимых
поверхностей. Однако в таком представление остаются многие
недостатки полигонального, например, задача поиска ребер,
инцидентных данной вершине по-прежнему требует полного перебора.
3.3 Список ребер
В такой модели грань представляется набором ребер и вершины
грани определяются через ребра.
|
Ребра |
Вершины |
Вершины |
Координаты |
Грани |
Ребра |
|
e1 |
v1 v2 |
v1 |
x1 y1 z1 |
f1 |
e1 e2 e3 e4 |
|
e2 |
v2 v3 |
v2 |
x2 y2 z2 |
f2 |
e9 e6 e1 e5 |
|
e3 |
v3 v4 |
v3 |
x3 y3 z3 |
f3 |
e10 e7 e2 e6 |
|
e4 |
v4 v1 |
v4 |
x4 y4 z4 |
f4 |
e11 e8 e7 e3 |
|
e5 |
v1 v5 |
v5 |
x5 y5 z5 |
f5 |
e12 e5 e4 e8 |
|
e6 |
v2 v6 |
v6 |
x6 y6 z6 |
f6 |
e12 e11 e10 e9 |
|
e7 |
v3 v7 |
v7 |
x7 y7 z7 |
||
|
e8 |
v4 v8 |
v8 |
x8 y8 z8 |
||
|
e9 |
v5 v6 |
||||
|
e10 |
v6 v7 |
||||
|
e11 |
v7 v8 |
||||
|
e12 |
v8 v5 |
Таким образом, для каждого ребра мы задаем направление.
Например, ребро e1 направлено ( имеет положительное направление) от
точки v1 к точке v2. Грани также ориентированы, т.е. ребра заданы по
часовой стрелке, если смотреть на куб снаружи.
3.4 Winged-Edge Representation ("крылатое" представление)
Эта модель является развитием модели, основанной на
информации о ребрах.
Отличие состоит в том, что в структуру,
описывающую ребра, добавляется информация о взаимном расположении
граней.
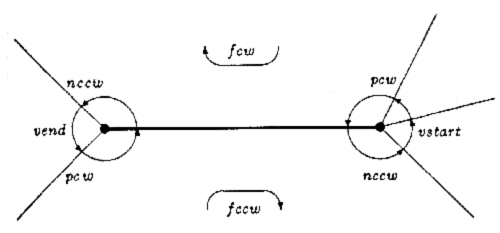
Рисунок 8 "Крылатое" представление
Так как каждое ребро e присутствует точно в двух гранях,
ровно два других ребра e1 и e2 появляются после e в этих гранях.
Более точно, поскольку направление обхода грани задано, e появляется
один раз в положительной ориентации, а другой раз – в
отрицательной.
"Крылатое представление" использует это путем
ассоциации с каждым ребром двух "следующих" ребер. Они обозначаются
как ncw и nccw ("next clockwise" и "next counterclockwise" ). В
данном случае ncw обозначает следующее ребро в той грани, где данное
ребро появляется в положительном направлении, а nccw – следующее
ребро в другой грани.
Таким образом, начиная с ребра, прямо
связанного с гранью, мы может получить все другие инцидентные данной
вершине ребра, следуя ссылкам ncw и nccw.
В наиболее общем случае
в нашу структуру включают также ссылки на предыдущие ребра в
соседних гранях. Имеем следующую структуру (см. рис):
struct
edge{
pEdge ncw, pcw, pccw, nccw;
pFace fcw, fccw;
pVertex
vstart, vend;
};
Здесь ncw, pcw – ссылки соответственно на
следующее и предыдущее ребро в грани, в которую данное ребро входит
в положительном направлении.
Аналогично nccw, pccw – следующее и
предыдущее ребро в грани, соответствующей отрицательному направлению
ребра.
3.5 Операции над граничными представлениями.
Рассмотрим операции, наиболее характерные для граничного
представления:
- проверка правильности задания
- вычисление габаритного объема
- вычисление нормали в точке
- вычисление кривизны поверхности
- нахождение точки пересечения с лучом или кривой
- определение положения точки относительно поверхности
Рассмотрим, например, алгоритм определения правильности
задания объекта.
3.5.1 Проверка правильности задания граничного представления
Известно соотношение, связывающее количество вершин, ребер
и граней в объекте – формула Эйлера.
В наиболее простом виде,
применимом для связных объектов без сквозных отверстий, она
записывается так:
V – E + F = 2,
где
V – количество
вершин
E – количество ребер
F – количество граней.
Для
произвольного объекта она выглядит
так:
V-E+F-H=2*(C-G),
где
H – количество отверстий
(несквозных).
C – количество компонент
G – количество сквозных
отверстий.
Например, для объекта на рисунке имеем следующее тождество:
24-36+15-3=2(1-1)
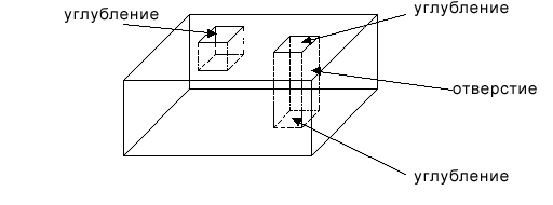
Рисунок 9 Пример
Формула Эйлера является
необходимым условием правильности задания сплошного (solid)
объекта.
4 Литература
- MARTTI MYNTYLA “An inroduction to solid modeling”