


2.3. Основные подпрограммы библиотеки Aztec
В состав библиотеки Aztec входит около 50 подпрограмм (функций в языке С), однако большая их часть имеет вспомогательный характер и в большинстве случаев не требуется прямое обращение к ним. Для корректного использования библиотеки требуется обращение к 5-6 подпрограммам. Рассмотрим их в соответствии с очередностью вызова этих подпрограмм в программах, основанных на библиотеке Aztec.
Функция идентификации процессоров AZ_processor_info
Эта функция является аналогом функции whoami в PSE и функций MPI_Comm_rank, MPI_Comm_size в MPI.
CALL AZ_processor_info(proc_config)
Информация возвращается в массив
integer proc_config(0:AZ_PROC_SIZE)
| IAM | = proc_config(AZ_node) | - | номер вызывающего процессора; |
| NPROCS | = proc_config(AZ_N_procs) | - | общее число процессоров, доступных программе. |
Функция рассылки информации по процессорам AZ_broadcast
Это аналог функции MPI_Bcast, ее реализация выполнена в стиле PVM: рассылаемая информация сначала упаковывается в системный буфер, а затем посылается одной командой. Рассылать может только 0-й процессор.
| CALL AZ_broadcast(n,4,proc_config,AZ_PACK) | - | упаковываем в буфер целую переменную n; |
| CALL AZ_broadcast(d,8,proc_config,AZ_PACK) | - | упаковываем в буфер переменную d типа real*8; |
| CALL AZ_broadcast(NULL,0,proc_config,AZ_SEND) | - | посылаем буфер. |
Функция определения параметров декомпозиции матрицы AZ_read_update
Определяет, сколько строк глобальной матрицы должно находиться в данном процессоре и номера этих строк.
CALL AZ_read_update(N_update, update, proc_config, nz, 1, 0)
| N_update | - | целая переменная, возвращает количество строк на процессоре; |
| update | - | целый массив размерности не меньше, чем N_update+1, возвращает номера строк в глобальной нумерации; |
| nz | - | размерность глобальной матрицы (входной параметр). |
Два последних параметра - константы.
После этого этапа в каждом процессоре должна быть сформирована размещенная в нем часть разреженной матрицы, представленная в виде двух массивов:
Этот этап целиком и полностью возлагается на программиста и требует от него некоторой
изобретательности.
Для VBR формата требуется сохранять больше информации (в данном пособии мы его рассматривать
не будем). Кроме того, должны быть сформированы векторы правых частей b и
начальное приближение решения x (только расположенные в данном процессоре части).
Функция преобразования глобальной индексации в локальную AZ_transform
CALL AZ_transform(proc_config, external, bindx, val, update,
$ update_index, extern_index, data_org,
$ N_update, NULL, NULL, NULL, NULL, AZ_MSR_MATRIX)
Входные параметры этой процедуры proc_config, bindx, val, update, N_update рассмотрены выше. Выходные параметры - целые массивы external, update_index, extern_index, data_org размерности не меньше, чем N_update + 1 - будут передаваться процедуре решения системы уравнений AZ_solve. Параметры, имеющие значения NULL, в случае MSR формата не используются.
Перед обращением к процедуре решения системы вектор правых частей и начальное приближение должны быть переопределены в соответствии с новой индексацией.
do i = 0, N_update - 1 xn(update_index(i)) = x(i) bn(update_index(i)) = b(i) end do
Функция инициализации предопределенных параметров решателя AZ_defaults
CALL AZ_defaults(options, params)
В данной процедуре оба параметра выходные и были подробно рассмотрены выше. Установки по умолчанию могут быть переопределены:
| options(AZ_solver)=AZ_cgs | - | выбор метода решения CGS; |
| options(AZ_precond)=AZ_dom_decomp | - | выбор переобуславливателя; |
| options(AZ_subdomain_solve)=AZ_ilu | - | неполное LU разложение; |
| options(AZ_output)=AZ_none | - | диагностику не выдавать; |
| options(AZ_max_iter)=1000 | - | максимальное число итераций 1000; |
| params(AZ_tol)=1.d-8 | - | критерий сходимости 10-8. |
Функция решения системы линейных алгебраических уравнений AZ_solve
Эта функция является основной "рабочей лошадкой" пакета.
CALL AZ_solve(xn, bn, options, params, NULL, bindx, NULL, NULL,
$ NULL, val, data_org, status, proc_config)
Параметры NULL не используются в случае MSR формата хранения матрицы. Выходными параметрами являются xn - распределенное по процессорам решение системы и рассмотренный выше массив status.
При использовании пакета Aztec самой сложной для программиста задачей является формирование надлежащим образом распределенной по процессорам матрицы.
На Рис. 10 представлен пример разреженной матрицы 6x6. Предположим, что мы хотим распределить ее в 3 процессора (нумерация процессоров с 0). Если бы мы воспользовались процедурой AZ_read_update, то, скорее всего, для каждого процессора N_update было бы установлено равным 2, и в массив update были бы соответственно занесены значения (0,1),(2,3),(4,5). Однако, для общности, рассмотрим реализацию другого варианта распределения. Пусть 0-й процессор хранит нулевую, первую и третью строки; 1-й процессор - одну четвертую строку; 2-й процессор - вторую и пятую строки. Этим самым мы однозначно задаем значения переменной N_update и массива update. Наша задача состоит в том, чтобы заполнить массивы bindx и val так, чтобы они адекватно описывали принятое распределение.
Массив val формируется следующим образом. Сначала в этот массив заносятся диагональные элементы хранимых строк, одна позиция пропускается (это сделано для соответствия с bindx) и затем, строка за строкой, в массив заносятся недиагональные ненулевые элементы (в том порядке, в котором они перечислены в массиве update).
В начале массива bindx хранятся номера позиций, с которых в массиве val начинаются недиагональные элементы соответствующей строки (включая и первую несуществующую - для того, чтобы можно было определить, сколько элементов в последней строке). Далее в массиве следуют номера столбцов, соответствующих ненулевым матричным элементам. Значения, которые должны быть занесены в соответствующие массивы в каждом процессоре, приведены ниже. Напоминаем, что индексация массивов начинается с 0.
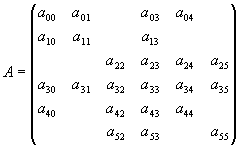
Рис. 10. Разреженная исходная матрица
| proc0: | |||||||||||||||
| N_update: | 3 | ||||||||||||||
| update: | 0 | 1 | 3 | ||||||||||||
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| bindx: | 4 | 7 | 9 | 14 | 1 | 3 | 4 | 0 | 3 | 0 | 1 | 2 | 4 | 5 | |
| val: | a00 | a11 | a33 | - | a01 | a03 | a04 | a10 | a13 | a30 | a31 | a32 | a34 | a35 | |
| _______________________________________________________________ | |||||||||||||||
| proc1: | ||||||
| N_update: | 1 | |||||
| update: | 4 | |||||
| index: | 0 | 1 | 2 | 3 | 4 | |
| bindx: | 2 | 5 | 0 | 2 | 3 | |
| val: | a44 | - | a40 | a42 | a43 | |
| ______________________________ | ||||||
| proc2: | |||||||||
| N_update: | 2 | ||||||||
| update: | 2 | 5 | |||||||
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| bindx: | 3 | 6 | 8 | 3 | 4 | 5 | 2 | 3 | |
| val: | a22 | a55 | - | a23 | a24 | a25 | a52 | a53 | |
| _________________________________________ | |||||||||
На практике, как было сказано выше, библиотека Aztec применяется для решения
систем линейных алгебраических уравнений, возникающих при решении
дифференциальных уравнений в частных производных. Для таких матриц, как
правило, заранее известно количество ненулевых матричных элементов в строке
и их местоположение в матрице, поэтому алгоритмы заполнения массивов val и
bindx бывают достаточно простые. В заключение рассмотрим пример программы,
в которой Aztec используется для решения системы уравнений, возникающей при
конечно-разностной аппроксимации 3-х мерного оператора Лапласа. Мы не будем
связывать систему ни с какой реальной физической задачей, а вместо этого
будем формировать правую часть таким образом, чтобы получить заранее известное решение, например,
x(i) = i + 1.
Пример 2.1. Программа решения разреженной системы линейных алгебраических уравнений с помощью библиотеки Aztec.
program Aztec
C Параметры:
C ndim - максимальное число неизвестных,
C lda - максимальный размер матрицы
parameter (ndim = 125000, lda = 7*ndim)
include 'mpif.h'
include 'az_aztecf.h'
integer n, nz
C
integer i, ierror, recb(0:63), disp(0:63)
double precision b(0:ndim), x(0:ndim), tmp(0:ndim)
double precision s, time, total
C
integer IAM, NPROCS
integer N_update
integer proc_config(0:AZ_PROC_SIZE), options(0:AZ_OPTIONS_SIZE)
integer update(0:ndim), external(0:ndim), data_org(0:ndim)
integer update_index(0:ndim), extern_index(0:ndim)
integer bindx(0:lda)
double precision params(0:AZ_PARAMS_SIZE)
double precision status(0:AZ_STATUS_SIZE)
double precision val(0:lda)
common /global/ n
C Инициализация MPI (для Aztec не обязательна, если не использовать
C MPI функции)
CALL MPI_Init(ierror)
C Получаем номер процессора и общее число процессоров,
C выделенных задаче
call AZ_processor_info(proc_config)
IAM = proc_config(AZ_node)
NPROCS = proc_config (AZ_N_procs)
C
C На 0-м процессоре печатаем пояснительную информацию и считываем
C параметр, определяющий размер решаемой задачи
C (максимально 50х50х50)
if (IAM.eq.0) then
write(6,2)
2 format(' '/
$ ' Aztec example driver'//
$ ' This program creates an MSR matrix corresponding to'/
$ ' a 7pt discrete approximation to the 3D Poisson operator'/
$ ' on an n x n x n square and solves it by various methods.'/
$ ' n must be <= 50.'//)
write (6,*) 'input number grid point on each direction n = '
read(*,*) n
endif
C Рассылаем считанный параметр всем процессорам
call MPI_BCAST(n, 1, MPI_INTEGER, 0, MPI_COMM_WORLD, ierr)
C Вычисляем количество неизвестных в системе
nz = n*n*n
C Цикл по всем методам решения
DO 777 K = 0,4
time = MPI_Wtime()
C Определяем параметры разбиения матрицы по процессорам
call AZ_read_update(N_update, update, proc_config, nz, 1, 0)
C Формируем матрицу в виде массивов val и bindx,
C в bindx(0) заносим номер позиции, с которой начнут располагаться
C недиагональные элементы, и выполняем цикл по всем строкам
bindx(0) = N_update+1
do 250 i = 0, N_update-1
call add_row_7pt(update(i), i, val, bindx)
250 continue
C Формируем правую часть системы таким образом, чтобы получить
C известное решениеа b(i) = 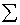 A(i,j)*j
C
do 341 i = 0, N_update-1
in = bindx(i)
ik = bindx(i+1) - 1
s = val(i)*(update(i)+1)
do 342 j = in,ik
s = s + val(j)*(bindx(j)+1)
342 continue
tmp(i) = s
341 continue
C Преобразуем глобальную индексацию в локальную
C
call AZ_transform(proc_config, external, bindx, val, update,
$ update_index, extern_index, data_org,
$ N_update, NULL,NULL,NULL,NULL, AZ_MSR_MATRIX)
C Устанавливаем параметры для решателя
call AZ_defaults(options, params)
options(AZ_solver) = K
options(AZ_precond) = AZ_dom_decomp
options(AZ_subdomain_solve) = AZ_ilu
options(4) = 1
options(AZ_output) = AZ_none
options(AZ_max_iter) = 2000
params(AZ_tol) = 1.d-10
C 0-й процессор печатает параметры решения задачи
if (IAM.eq.0) then
write(6,780)
write (6,*) ' The solution of method is =',К
write (6,*) ' Dimension matrices =',nz,
$ ' NPROCS = ', NPROCS
endif
C Преобразуем правую часть в соответствии с новой индексацией
do 350 i = 0, N_update-1
x(update_index(i)) = 0.0
b(update_index(i)) = tmp(i)
350 continue
C Решаем систему уравнений
call AZ_solve(x,b, options, params, NULL,bindx,NULL,NULL,
$ NULL, val, data_org, status, proc_config)
C Полученное решение возвращаем к исходной индексации
DO 415 I = 0,N_update - 1
415 tmp(i) = x(update_index(i))
C
C Выполняем сборку полученных частей решения в один вектор на 0-м процессоре
C
CALL MPI_ALLgather(N_update, 1, MPI_INTEGER, recb, 1,
$ MPI_INTEGER, MPI_COMM_WORLD, ierror)
DISP(0) = 0
DO 404 I = 1,NPROCS-1
404 DISP(I) = DISP(I-1) + RECB(I-1)
CALL MPI_ALLgatherv(tmp, N_update, MPI_DOUBLE_PRECISION, x, recb,
$ disp, MPI_DOUBLE_PRECISION, MPI_COMM_WORLD, ierror)
C
C Печатаем первую и последнюю компоненты решения
nz1 = nz-1
if (IAM.eq.0) then
do 348 i = 0,nz1,nz1
s = x(i)
write (6,956) i,s
348 continue
956 format (2x,'i=',I12,2x,'x(i)=',F18.8)
endif
C
time = MPI_Wtime() - time
C
if(IAM.eq.0) write(*,435) time
435 FORMAT(2x,'TIME CALCULATION (SEC.) = ',F12.4)
777 continue
C
CALL MPI_FINALIZE(IERROR)
stop
end
C Подпрограмма добавления очередной строки в массивы val и bindx
subroutine add_row_7pt(row, location, val, bindx)
integer row, location, bindx(0:*)
double precision val(0:*)
integer n3,n,k
common /global/ n
C Входные параметры:
C row == глобальный номер добавляемой строки
C location == локальный номер строки в процессоре
C n3 - максимально возможный номер столбца
n3 = n*n*n - 1
C Далее выполняется проверка: существует ли в трехмерной решетке
C ближайший сосед по каждому из направлений; если да, то
C соответствующий матричный элемент заносится и
C счетчик увеличивается на 1
k = bindx(location)
bindx(k) = row + 1
if (bindx(k).le.n3) then
val(k) = -1.
k = k + 1
endif
bindx(k) = row - 1
if (bindx(k) .ge. 0) then
val(k) = -1.
k = k + 1
endif
bindx(k) = row + n
if (bindx(k).le.n3) then
val(k) = -1.0
k = k + 1
endif
bindx(k) = row - n
if (bindx(k).ge. 0) then
val(k) = -1.0
k = k + 1
endif
bindx(k) = row + n*n
if (bindx(k) .le. n3) then
val(k) = -1.0
k = k + 1
endif
bindx(k) = row - n*n
if (bindx(k) .ge. 0) then
val(k) = -1.0
k = k + 1
endif
C Занесение диагонального матричного элемента
val(location) = 6.0
C Подготовка следующего шага: заносим номер позиции, с которой
C будут располагаться недиагональные элементы следующей строки
bindx(location+1) = k
return
end
A(i,j)*j
C
do 341 i = 0, N_update-1
in = bindx(i)
ik = bindx(i+1) - 1
s = val(i)*(update(i)+1)
do 342 j = in,ik
s = s + val(j)*(bindx(j)+1)
342 continue
tmp(i) = s
341 continue
C Преобразуем глобальную индексацию в локальную
C
call AZ_transform(proc_config, external, bindx, val, update,
$ update_index, extern_index, data_org,
$ N_update, NULL,NULL,NULL,NULL, AZ_MSR_MATRIX)
C Устанавливаем параметры для решателя
call AZ_defaults(options, params)
options(AZ_solver) = K
options(AZ_precond) = AZ_dom_decomp
options(AZ_subdomain_solve) = AZ_ilu
options(4) = 1
options(AZ_output) = AZ_none
options(AZ_max_iter) = 2000
params(AZ_tol) = 1.d-10
C 0-й процессор печатает параметры решения задачи
if (IAM.eq.0) then
write(6,780)
write (6,*) ' The solution of method is =',К
write (6,*) ' Dimension matrices =',nz,
$ ' NPROCS = ', NPROCS
endif
C Преобразуем правую часть в соответствии с новой индексацией
do 350 i = 0, N_update-1
x(update_index(i)) = 0.0
b(update_index(i)) = tmp(i)
350 continue
C Решаем систему уравнений
call AZ_solve(x,b, options, params, NULL,bindx,NULL,NULL,
$ NULL, val, data_org, status, proc_config)
C Полученное решение возвращаем к исходной индексации
DO 415 I = 0,N_update - 1
415 tmp(i) = x(update_index(i))
C
C Выполняем сборку полученных частей решения в один вектор на 0-м процессоре
C
CALL MPI_ALLgather(N_update, 1, MPI_INTEGER, recb, 1,
$ MPI_INTEGER, MPI_COMM_WORLD, ierror)
DISP(0) = 0
DO 404 I = 1,NPROCS-1
404 DISP(I) = DISP(I-1) + RECB(I-1)
CALL MPI_ALLgatherv(tmp, N_update, MPI_DOUBLE_PRECISION, x, recb,
$ disp, MPI_DOUBLE_PRECISION, MPI_COMM_WORLD, ierror)
C
C Печатаем первую и последнюю компоненты решения
nz1 = nz-1
if (IAM.eq.0) then
do 348 i = 0,nz1,nz1
s = x(i)
write (6,956) i,s
348 continue
956 format (2x,'i=',I12,2x,'x(i)=',F18.8)
endif
C
time = MPI_Wtime() - time
C
if(IAM.eq.0) write(*,435) time
435 FORMAT(2x,'TIME CALCULATION (SEC.) = ',F12.4)
777 continue
C
CALL MPI_FINALIZE(IERROR)
stop
end
C Подпрограмма добавления очередной строки в массивы val и bindx
subroutine add_row_7pt(row, location, val, bindx)
integer row, location, bindx(0:*)
double precision val(0:*)
integer n3,n,k
common /global/ n
C Входные параметры:
C row == глобальный номер добавляемой строки
C location == локальный номер строки в процессоре
C n3 - максимально возможный номер столбца
n3 = n*n*n - 1
C Далее выполняется проверка: существует ли в трехмерной решетке
C ближайший сосед по каждому из направлений; если да, то
C соответствующий матричный элемент заносится и
C счетчик увеличивается на 1
k = bindx(location)
bindx(k) = row + 1
if (bindx(k).le.n3) then
val(k) = -1.
k = k + 1
endif
bindx(k) = row - 1
if (bindx(k) .ge. 0) then
val(k) = -1.
k = k + 1
endif
bindx(k) = row + n
if (bindx(k).le.n3) then
val(k) = -1.0
k = k + 1
endif
bindx(k) = row - n
if (bindx(k).ge. 0) then
val(k) = -1.0
k = k + 1
endif
bindx(k) = row + n*n
if (bindx(k) .le. n3) then
val(k) = -1.0
k = k + 1
endif
bindx(k) = row - n*n
if (bindx(k) .ge. 0) then
val(k) = -1.0
k = k + 1
endif
C Занесение диагонального матричного элемента
val(location) = 6.0
C Подготовка следующего шага: заносим номер позиции, с которой
C будут располагаться недиагональные элементы следующей строки
bindx(location+1) = k
return
end