Источник:
Орлов Ю.К., Мокрый Г.В. "Методические рекомендации по использованию методов линейного программирования при создании комплексной автоматизированной системы информации": Д, 1990, 92с.

ПОИСК ОПОРНОГО РЕШЕНИЯ

    Поиск опорного решения симплекс-методом состоит в следующем.
    Просматриваем столбец свободных членов. Если все коэффициенты этого столбца не отрицательны, можно подучить сразу опорное решение путем приравнивания к нулю переменных, стоящих в верхней части таблицы . Тогда переменные находящиеся в левом столбце симплекс-таблицы принимают значения элементов столбца свободных членов. А поскольку последние неотрицательны, это решение удовлетворяет исходным ограничениям. В соответствии с уравнением:

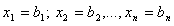получим . Значение целевой функции .
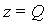    Пусть некоторые 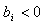. В этом случае приравнивание к нулю переменных верхней части таблицы не дает опорного решения, так как при этом . Это решение определяет лишь точку пересечения n плоскостей, лежащую вне области допустимых решений.
    Поиск опорного решения сводится к переходу от данной вершины к такой соседней, которая отделяется от области допустимых решений меньшим числом плоскостей, то есть в таблице содержится меньшее число отрицательных свободных членов.
    Выберем любой отрицательный элемент. Пусть . В качестве направления движения должна быть выбрана ось, которая приблизила бы нас к отделяющей плоскости, то есть должно выполняться условие:

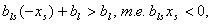
а, поскольку неотрицательно, то .
    Таким образом, в строке с отрицательным выбираем отрицательный коэффициент . Данный столбец берется в качестве разрешающего. Если в l-ой строке нет отрицательных коэффициентов, то движение к отделяющей плоскости невозможно ни по одной из осей. Это и является признаком несовместности системы уравнений.
    Для выбора разрешающей строки определяем неотрицательные отношения свободных членов к соответствующим, отличным от нуля, коэффициентам разрешающего столбца. Из них выбираем наименьшее. Пусть это соотношение соответствует r-ой строке. Тогда элемент 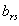будет разрешающим, и с ним проделываем шаг модифицированных жордановых исключений. Если разрешающий элемент лежит в строке с отрицательным свободным членом, то новый свободный член будет уже положительным. В противном случае вновь возвращаемся на просмотр строки с отрицательным свободным членом.
    Описанную процедуру продолжаем до тех пор, пока не исключим из столбца свободных членов отрицательные элементы или не убедимся в несовместимости исходной системы уравнений.