УДК 621.313.323

Донецк, ДонНТУ

РАСЧЕТ НЕСИММЕТРИЧНЫХ РЕЖИМОВ АД С ПОМОЩЬЮ ЧАСТОТНЫХ ХАРАКТЕРИСТИК

У даній статті розглядаються питання розрахунку несиметричних режимів асинхронних двигунів із використанням їх частотних характеристик. Наведена послідовність розрахунку по частотним характеристикам струму ввімкнення двигуна на дві фази. Показано, що результати розрахунків добре співпадають із експериментальними даними.

В этой статье рассматриваются вопросы расчета несимметричных режимов асинхронных двигателей с использованием их частотных характеристик. Приведена последовательность расчета по частотным характеристикам тока включения двигателя на две фазы. Показано хорошее совпадение результатов с экспериментальными данными.

Исследованию и расчету несимметричных режимов в синхронных (СМ) и асинхронных (АМ) машинах посвящено большое количество работ отечественных и зарубежных ученых. Однако до сих пор остается проблема обеспечения точности и простоты получения решения одновременно. В ранних работах [Догерти, Найкл, Конкордиа, Лайон] несимметричные короткие замыкания (КЗ) исследовались с использованием метода постоянства потокосцеплений обмоток, простого и дающего достаточно точные для практики результаты, но имеющего ограниченную область применения. Проводились неоднократные попытки [Трещев, Лупкин] составить и решить дифференциальные уравнения машины для несимметричных режимов, подобные уравнениям Парка-Горева. Однако полученные таким образом уравнения либо оказывались чрезвычайно сложными, либо так и не были доведены до формул, пригодных для употребления на практике. На сегодняшний день наилучшие результаты дают методы расчета, основанные на нахождении поля в воздушном зазоре машины (например, метод проводимости зубцовых контуров), однако они требуют составления больших систем нелинейных дифференциальных уравнений, решение которых может быть получено только численными методами и требует больших затрат труда и машинного времени. Расчет переходных процессов, основанный на численном интегрировании дифференциальных уравнений машины, дает хорошие результаты при исследовании электромагнитных и электромеханических переходных процессов в случае симметричных режимов. Однако для случая несимметричных режимов прямое решение дифференциальных уравнений Парка-Горева невозможно из-за появления периодических коэффициентов; кроме того, учет многоконтурности ротора, насыщения машины, внешних сопротивлений в цепи статора либо вообще невозможен, либо весьма затруднен.

Хорошей альтернативой вышеупомянутым подходам является частотный метод, основанный на использовании частотных характеристик (ЧХ) асинхронной либо синхронной машины. Он достаточно прост, нагляден, не требует составления и решения системы дифференциальных уравнений машины и может быть применен к расчету как симметричных, так и несимметричных режимов. На кафедре электрических систем ДонНТУ разработана методика расчета переходных процессов при симметричных коротких замыканиях и включениях в сеть синхронных и асинхронных машин, основанная на использовании частотных характеристик [2].

Целью данной работы является разработка методики расчета несимметричных режимов работы асинхронного двигателя (АД) с использованием ЧХ.

В соответствии с поставленной целью можно выделить следующие задачи:

- установление взаимосвязи ЧХ с физической картиной при несимметричных режимах работы АД;

- получение математических соотношений для расчета переходных процессов при несимметричных коротких замыканиях и неполнофазных включениях АД в сеть;

- проверка правильности разработанной методики путем сравнения экспериментальных результатов и результатов математического моделирования для случая включения АД в сеть на две фазы.

Частотная характеристика машины представляет собой зависимость комплексной проводимости со стороны статора от скольжения ротора Y(js). При напряжении на выводах АД, равном единице, проводимость численно равна току статора в относительных единицах, что позволяет по известной ЧХ непосредственно определить ток статора для любого скольжения. Принципиально с использованием ЧХ можно рассчитать любой переходный процесс машины [3], в том числе и при возникновении несимметричных режимов работы.

Несимметричные режимы машины (однофазное и двухфазное короткие замыкания (КЗ), включение на две фазы, обрыв одной фазы) вызывают появление токов обратной последовательности и приводят к возникновению в обмотках статора и ротора теоретически бесконечного спектра четных и нечетных гармоник [4], обусловленному различием электромагнитных свойств ротора по осям d и q. Однако в случае АД, имеющего симметричный ротор, высшие гармоники не возникают, кроме второй гармоники в статоре, вызванной прямовращающейся составляющей поля обмотки ротора.

Довольно важным вопросом является способ представления несимметричного режима. Как известно [5], несимметричные КЗ можно представить как включение в месте КЗ некоторой системы напряжений, равных по модулю и направленных противоположно тем, что были в исходном режиме. Так, например, однофазное КЗ фазы А на нейтраль равносильно включению на напряжение –U_А, двухфазное КЗ фаз В и С – включению на напряжение –(U_B-U_C). Однако для анализа переходных процессов удобнее представлять несимметричные режимы как включения на симметричные трехфазные системы напряжений прямой (ПП) и обратной (ОП) последовательностей, определяемых согласно методу симметричных составляющих. Следует отметить, что методика определения токов и моментов машины при включении ее на симметричную систему напряжений уже разработана [2] и ее можно применить и для расчета несимметричных режимов.

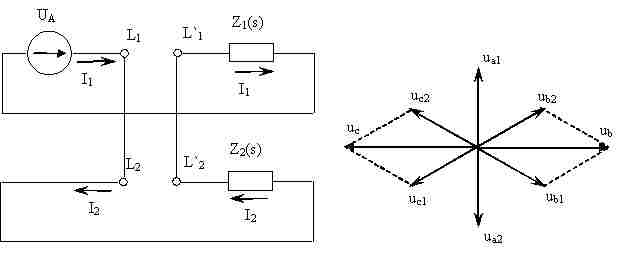
При использовании метода симметричных составляющих необходимо учитывать, что величины напряжений ПП и ОП меняются в течение переходного процесса [5,6,7]. Это изменение легко пояснить с использованием рис.1.

Рис. 1. К объяснению зависимости напряжений ПП и ОП от скольжения

В [8] предлагается раскладывать токи статора на равные по модулю составляющие ПП и ОП, неизменные в течение переходного процесса, а напряжения этих последовательностей находить через токи статора и сопротивления Z₁(s) и Z₂(s). На кафедре электрических систем ДонНТУ был разработан другой подход к решению этой проблемы, позволяющий непосредственно применить частотный метод расчета к несимметричным режимам. В соответствии с ним, ток ПП при возникновении несимметричного режима рассчитывается как ток включения на симметричную систему напряжений ПП, если в схему замещения АД включить дополнительное сопротивление согласно правилу Н.Н.Щедрина (см. рис.2).

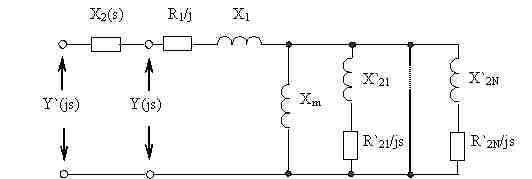
Рис. 2. Включение сопротивления Х₂ для расчета частотным методом

Так, например, при включении АД на две фазы или двухфазном КЗ необходимо последовательно к схеме замещения ПП включить схему замещения ОП или сопротивление ОП X₂(s). Поскольку сопротивление ОП АД сравнительно слабо зависит от скольжения, то в первом приближении можно считать X₂=const.

Расчет токов и моментов АД осуществляется в следующем порядке.

Рассчитывается частотная характеристика с учетом сопротивления ОП:

.

Установившийся ток КЗ:

,

где .

Апериодическая составляющая тока КЗ:

,

где

,

а величины ω_с и Т_а могут быть непосредственно найдены по ЧХ:

, .

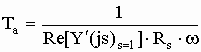Начальное значение переходного периодического тока I_s2(t) определяется из уравнения:

,

а сам ток I_s2(t) находится так:

,

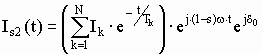где I_k, T_k - начальные значения и постоянные времени экспоненциальных составляющих, аппроксимирующих огибающие периодических токов; N - количество роторных контуров, - угол между поперечной осью ротора и вектором напряжения сети.

Изображающий вектор тока статора:

,

где U - напряжение на выводах статора АД.

Составляющие ПП и ОП фазных токов:

, ;

, ;

, .

Полные фазные токи:

;

;

.

Электромагнитный момент:

,

где

.

Проверка правильности предлагаемой методики выполнялась путем сравнения результатов опытов включения АД на две фазы с результатом расчета токов статора по предлагаемой методике и методом численного решения полных уравнений Парка-Горева. Испытания проводились на асинхронном двигателе типа 4А90 (Р_Н=2,2кВт, U_H=380/220В, I_H=4,9/8,6A). Параметры Г-образной схемы замещения двигателя:

; ; ; ; .

На рис.3 приведены кривые токов в фазах В и С при включении АД на две фазы (графики 1 и 2 – кривые, полученные в результате решения уравнений Парка-Горева при включении последовательно с схемой замещения ПП сопротивления Х₂=0,2; графики 3 и 4 – экспериментальные осциллограммы при включении АД в сеть; графики 5 и 6 – кривые фазных токов, рассчитанные по предлагаемой методике). Опыт производился при пониженном напряжении (150В), что позволило избежать влияния насыщения на измеряемые величины. Как видно из рисунка, имеет место достаточно хорошее совпадение расчетных и экспериментальных кривых в обоих фазах; максимальное отклонение не превышает 5%, из чего можно сделать вывод, что предлагаемая методика достаточно точно отображает процессы в двигателе.

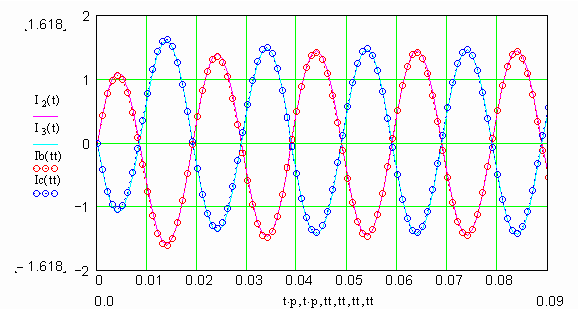
Рис. 3. Осциллограммы фазных токов при включении двигателя 4А90 на две фазы

Кроме того, производилось математическое моделирование включения на две фазы асинхронного двигателя АО 51-2 (Р_Н=4,5кВт, U_H=380В, I_H=8,9A). Параметры двухконтурной Т-образной схемы замещения двигателя:

; ; ;

; ;;

На рис. 4 приведены графики фазных токов двигателя, рассчитанные по уравнениям Парка-Горева (кривые 1 и 2) и по частотным характеристикам (кривые 3 и 4). Как можно видеть, и в случае двигателя, представляемого двухконтурной схемой замещения, погрешность расчета достаточно мала (не более 5%).

Исследования, проведенные на двигателе 4А90, показали, что в случае маломощного двигателя (который можно представить одноконтурной схемой замещения) вышеописанная методика дает хорошее совпадение результатов расчета и экспериментальных данных, позволяя легко учитывать активное сопротивление статора и внешние сопротивления. Если же в схемах замещения необходим учет многих контуров (мощные АД, синхронные генераторы), то методика усложняется, поскольку при добавлении сопротивлений в цепь статора возникает необходимость пересчета параметров роторных контуров схемы замещения. В дальнейшем планируется усовершенствовать предлагаемую методику для расчета с ее помощью несимметричных режимов машин, представляемых многоконтурными схемами замещения, в частности, синхронных генераторов, а также многомашинных систем.

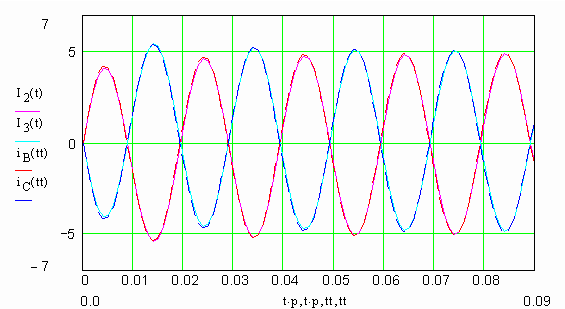
Рис. 4. Осциллограммы фазных токов при включении двигателя АО 51-2 на две фазы

Литература

1. Универсальный метод расчета электромагнитных процессов в электрических машинах / А.В.Иванов-Смоленский, Ю.В.Абрамкин, А.И.Власов, В.А.Кузнецов. – М.: Энергоатомиздат, 1986. – 216с.
2. Ларин А.М., Ларина И.И., Гуедиди Фаузи. Упрощенная модель синхронной машины для расчета трехфазных коротких замыканий с учетом многоконтурности и несимметрии ротора. Научные труды ДонГТУ, серия Электротехника и энергетика, вып.
3. - Донецк. - 1999. - С. 60-64. 3. Брынский Е.А. Определение частотных характеристик гидрогенератора СВ-1500/200-88. – В кн. Теория, расчет и исследование высокоиспользованных электрических машин. – М.-Л.: Наука, 1965. – С. 85 – 94.
4. Важнов А. И. Переходные процессы в машинах переменного тока. -Л.:Энергия, 1980. -256с.
5. Казовский Е.Я.Переходные процессы в электрических машинах переменного тока.-Л.:Энергия, 1962.-624с. 6. Казовский Е.Я., Рубисов Г.В. Переходные процессы в синхронных машинах при анормальных режимах в энергосистеме. - СПб.: Наука, 1994. - 172с.
7. Казовский Е.Я., Рубисов Г.В. Внезапные несимметричные КЗ синхронной машины, включенной в мощную сеть // Исследование турбо- и гидрогенераторов большой мощности. -Л.: Наука, 1977.- с. 67-84.
8. Кононенко Е.В., Кононенко К.Е., Кружков В.Г. Анализ работы асинхронных двигателей при несимметрии первичного напряжения // Изв. вузов.- Электромеханика. - 2000. - №1. - с.30-36.