Статья Особенности дуговых замыканий фазы на землю в сетях с нейтралью, заземленной через резистор

ОСОБЕННОСТИ ДУГОВЫХ ЗАМЫКАНИЙ ФАЗЫ НА ЗЕМЛЮ В СЕТЯХ С НЕЙТРАЛЬЮ, ЗАЗЕМЛЕННОЙ ЧЕРЕЗ РЕЗИСТОР

В энергетике страны в последние годы появились сети 6—10 кВ с нейтралью, заземленной через токоограничивающий резистор. К числу таких сетей относятся сети собственного расхода энергоблоков ГРЭС [1] и сети горных карьеров [2]. Однако выбор сопротивления резистора в этих случаях производился на практике, либо экспериментально [I], либо по весьма упрощенным соотношениям [2], что исключает возможность максимальной реализации преимуществ таких сетей, заключающихся в снижении уровней перенапряжений при дуговых замыканиях и повышении функциональной надежности защит от замыканий на землю. Объясняется это недостаточной изученностью процессов, происходящих в сети при замыканиях фазы на землю, и прежде всего дуговых процессов в широком диапазоне возможного изменения параметров сети. Это обстоятельство затрудняет объяснение осциллограмм, получаемых в реальных сетях, в том числе и осциллограмм, приведенных в [I]. Авторы этой статьи справедливо отмечают, что с изменением сопротивления заземляющего резистора меняется характер дуговых замыканий, но не разъясняют, в чем заключается это изменение.

В [3] было показано, что процессы дугового замыкания в указанных условиях целесообразно исследовать методами численного анализа с использованием ЭВМ. Математическая модель была получена на базе упрощенной схемы замещения сети, в которой не были учтены трансформатор напряжения и междуфазные емкости. В сетях с относительно небольшим током замыкания, т. е. с малой емкостью фаз по отношению к земле (а такой сетью является сеть б кВ энергоблока). Трансформаторы напряжения типа НТМИ могут существенно влиять на переходные процессы. В случае заземления нейтрали сети через резистор, сопротивление которого соизмеримо с емкостным сопротивлением фаз по отношению к земле, феррорезонансные процессы не 'исключаются полностью, а становятся затухающими. Поэтому трансформаторы напряжения типа НТМИ и в таких сетях существенно влияют на переходные процессы независимо от сопротивления резистора. Междуфазные емкости сети могут заметно влиять на перенапряжения и также должны учитываться при их оценке. Хотя в [3] и получены полезные практические выводы, авторы сочли необходимым разработать более универсальную математическую модель, которая позволила бы более достоверно отразить реальные условия в сетях 6 кВ энергоблоков.

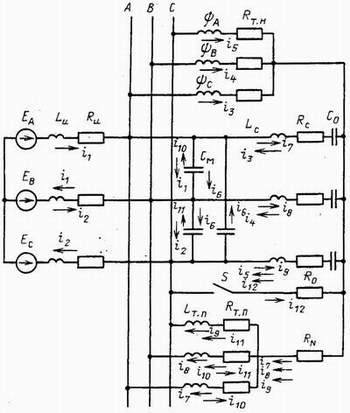
Рисунок 1 - Схема замещения сети 6 кВ собственного расхода энергоблока в режиме замыкания фазы на землю

На рис.1 представлена схема замещения одной из секций 6 кВ собственного расхода энергоблока 500 МВт, для которой были получены осциллограммы, приведенные в [I]. В этой схеме источник, питающий секцию шин (трансформатор типа ТРДНС-40), представлен фазными значениями индуктивности рассеяния L_И и сопротивления R_И. Сеть, присоединенная к секции, отражена сосредоточенными фазной С_о и междуфазной С_М емкостями и эквивалентной индуктивностью L_c. Токоограничивающий резистор R_N включен в сеть через нейтраль присоединительного трансформатора (ТСЗК-60/10) с фазными значениями активного сопротивления R_Т.П и индуктивности L_Т.П. Трансформатор напряжения типа НТМИ-6-0,66 представлен активным сопротивлением R_Т.Н и потокосцеплениями Y, зависящими от тока.

Исходная математическая модель в данном случае аналогична приведенным в [3, 4], поэтому здесь ограничимся только общей характеристикой. В соответствии с контурными токами, показанными на рис.1, математическая модель в режиме замыкания фазы на землю (ключ S замкнут) представляет собой систему из 12 дифференциальных уравнений, а в режиме бестоковой паузы (ключ S разомкнут) — из 11 уравнений. Реализация этой модели на ЭВМ в режиме дугового замыкания осуществлялась путем последовательного решения указанных систем уравнений с использованием стандартной программы RKGS, основанной на методе Рунге — Кутта четвертого порядка [4]. Принятый алгоритм позволяет задавать любые реально возможные значения пробивного напряжения дугового промежутка, а обрыв дуги осуществлять при любом номере перехода через нуль тока, протекающего в месте повреждения. Это обеспечивает возможность косвенного моделирования практически любых реальных условий дуговых промежутков, в том числе и для скорости восстановления электрической прочности.

Числовые параметры схемы замещения были рассчитаны исходя из параметров реального оборудования [4] и составили L_И = 6,35× 10^-4 Гн, R_И = 0,0633 Ом, L_c = 0.635× 10^-4 Гн, R_c = 0,014 Ом, L_Т.П = 0.13 Гн, R_Т.П = 10 Ом. Максимальное фазное напряжение Е_m было определено по осциллограммам, приведенным в [1], и составило 4740 В. Было также принято: С_М = 1/3 С_о (для кабельных сетей), R_о = 4 Ом (сопротивление заземляющего контура).

В [1] на рис.2 была приведена осциллограмма, полученная при замыкании фазы на землю в сети собственного расхода б кВ блока 500 МВт, заземленной через резистор 134 Ом. Алгоритм процессов, зафиксированных на этой осциллограмме, сводится к следующему: замыкание фазы С на землю произошло в момент, когда напряжение этой фазы близко к нулю, затем после трех полупериодов глухого замыкания с током 33,5 А в момент прохождения тока через нуль произошел обрыв связи фазы с землей и в момент, когда напряжение U_C достигло значения порядка 3,5 кВ, произошел пробой дугового промежутка, перешедший практически в глухое замыкание, так как имевшие место последующие кратковременные обрывы связи фазы с землей сопровождались пробоями при очень малом напряжении практически без переходных процессов.

На рис.2 приведены расчетные кривые, полученные при реализации модели с учетом описанного выше алгоритма и указанных параметров. Сопоставляя расчетные кривые с осциллограммой в [1], можно убедиться в хорошем качественном и количественном совпадении, что подтверждает достаточную достоверность разработанной модели. Следует отметить, что в алгоритм расчета кратковременные обрывы связи фазы с землей не вводились.

Рис. 2. Расчетные кривые токов и напряжений при дуговом замыкании в сети с R_N = 134 Ом

На рис.3 приведены расчетные кривые токов и напряжений при дуговом замыкании для условий. в которых была получена осциллограмма, приведенная на рис.1 в [1], т. е. при R_N = R_заз = 227 Ом. На указанной осциллограмме после трех пробоев в начальной стадии зафиксирован процесс стабильного перемежающегося (дугового) замыкания с четко выраженными сериями кратковременных пробоев дугового промежутка. Каждая серия пробоев начинается пробоем промежутка при U_пр = 4,7 кВ, затем при очередных переходах тока через нуль напряжение за время порядка 0,65 мс нарастает до 1,5—3,0 кВ и происходит новый пробой. В связи с этим в алгоритм численной реализации дугового замыкания было внесено дополнение, заключающееся в том, что после первого пробоя дугового промежутка при U_пр = 4,7 кВ было введено условие: если напряжение, восстанавливающееся на дуговом промежутке, достигает значения 2 кВ менее, чем за 1 мс, то пробивное напряжение принимается равным 2 кВ, если же за это время напряжение нарастает менее чем до 2 кВ, то пробивное напряжение принимается равным 4,7 кВ. Сопоставляя расчетные кривые на рис.3 с кривыми осциллограммы [1], можно видеть, что и в расчетном случае пробои дугового промежутка представляют собой серии кратковременных пробоев.

Следует отметить, что реализация модели при неизменном значении U_пр = 4,7 кВ показала: дуговое замыкание и в этом случае представляет собой серии пробоев, отличающиеся от изображенных на рис.3 и на осциллограмме соответственно большими всплесками напряжения и меньшим числом пробоев в каждой серии.

На расчетную кривую напряжения U_C фазы C относительно земли на рис.3 наложена пунктирная синусоида, отражающая ЭДС этой фазы. Нетрудно видеть закономерность, заключающуюся в том, что каждая серия пробоев начинается в момент, когда близок максимум ЭДС источника, поэтому наложение свободной составляющей напряжения на большие мгновенные значения ЭДС в сочетании с быстрым затуханием напряжения на нейтрали обуславливает быстрое нарастание восстанавливающегося напряжения.

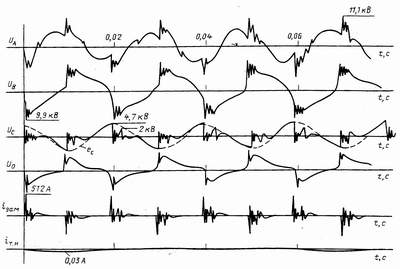
Рисунок 3 - Расчетные кривые токов и напряжений при дуговом замыкании в сети с R_N = 227 Ом

При этом электрическая прочность промежутка не успевает достигать больших значений, и пробои происходят при 1,5—3,0 кВ. К концу серии пробоев ЭДС существенно снижается, скорость нарастания напряжения на промежутке уменьшается, дуга обрывается и бестоковая пауза длится до следующего максимума ЭДС.

На осциллограмме (рис.1 в [1]) наибольшее зафиксированное напряжение в фазе А составило 2,3U_m = 10,9 кВ, а на расчетных кривых - 11 кВ, что также подтверждает достоверность модели. Следует отметить, что ток в месте замыкания представляет собой серии высокочастотных импульсов с максимальной амплитудой до 512 А (расчет). Практическое отсутствие тока замыкания на осциллограмме в интервале пробоя промежутка объясняется чрезмерной перегрузкой гальванометра осциллографа.

Таким образом, проведенное выше сопоставление расчетных кривых с экспериментальными не только подтвердило достоверность численного анализа дуговых замыканий, но и позволило объяснить процессы, записанные на реальных и, соответственно, технически несовершенных осциллограммах.

При численной реализации алгоритма дугового замыкания в конкретной сети возникает необходимость оценки номера перехода тока в месте замыкания через нуль, при котором реально возможно погасание дуги. Необходимо также предварительно оценить и максимально возможное пробивное напряжение, которое определяется напряжением, восстанавливающимся на дуговом промежутке. Расчетные кривые тока в месте замыкания показывают, что в исследуемой сети даже при R_N = 20 Ом (рис.4, а) свободная составляющая имеет явно выраженный периодический характер, т. е. высокочастотный ток многократно переходит через нуль. Это означает, что в данной сети независимо от реально возможного значения сопротивления заземляющего резистора возможность погасания дуги практически существует при первом и последующих переходах через нуль высокочастотной и вынужденной составляющих. Увеличение R_N (рис. 4, б) практически не влияет на максимальную амплитуду свободного тока, так как в нем преобладает емкостная составляющая, но увеличивает число переходов тока через нуль и уменьшает установившееся значение тока. Это означает, что в данной сети, в отличие от других сетей [З], не существует реального значения сопротивления заземляющего резистора, при котором обрыв дуги возможен только при переходе через нуль вынужденной составляющей тока.

На рис.4, в, г, д представлены расчетные кривые напряжения, восстанавливающегося на поврежденной фазе при обрыве дуги в момент второго (М=2), третьего (М=3) и пятого (М=5) переходов тока в месте замыкания через нуль в сети с R_N = 227 Ом. Эти кривые показывают, что с увеличением номера перехода тока через нуль первый максимум напряжения U_C уменьшается. Обусловлено это тем, что с увеличением номера перехода в момент обрыва напряжение U₀ оказывается меньше, а это указывает на меньший уровень избыточной энергии, запасенной емкостями сети; соответственно, амплитуды свободных составляющих уменьшаются, что и приводит к уменьшению результирующего напряжения.

В первом случае (рис.4, а) напряжение за 2,5 мс возросло до 38 кВ и средняя скорость нарастания составила 15,2 кВ/мс. Из осциллограммы на рис.1 в [1] следует, что при попытках обрыва дуги пробои происходили при 1,5—3,0 кВ. Это означает, что за время порядка 0,65 мс электрическая прочность реального дугового промежутка успевала вырасти до этих значений. В конце интервала времени происходил пробой, так как восстанавливающееся напряжение становилось равным пробивному. Это дает основание принять в первом приближении среднюю скорость увеличения пробивного напряжения равной средней скорости нарастания напряжения на промежутке, что для указанной осциллограммы составляет 2,3-4,6 кВ/мс.

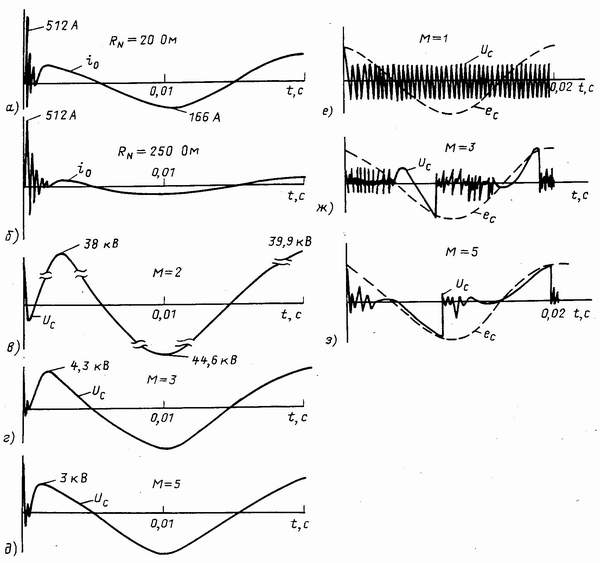
Рисунок 4 - Расчетные кривые токов в месте замыкания и напряжений на поврежденной фазе после обрыва тока дуги: а, б - ток в месте замыкания; в, г, д - напряжение на поврежденной фазе после обрыва тока дуги в сети с R_N = 227 Ом; е, ж, з - напряжение на поврежденной фазе в режиме дугового замыкания в сети с R_N = 134 Ом

Хотя средние скорости рассмотренных процессов не отражают истинную картину, сопоставление полученных данных позволяет сделать достаточно достоверный вывод о том, что в данной сети обрыв дуги невозможен при втором переходе тока через нуль. Тем более он невозможен при первом переходе, так как в этом случае скорость восстановления напряжения на дуговом промежутке будет еще большей. Расчетные значения средней скорости восстановления напряжения на дуговом промежутке составили 2,46 кВ/мс в случае обрыва дуги при третьем и 1,7 кВ/мс при пятом переходах тока через нуль. Это означает, что вероятность обрыва дуги при третьем и тем более при пятом переходах тока через нуль существенно увеличивается.

Аналогичные исследования показали, что с уменьшением R_N скорость нарастания напряжения на дуговом промежутке уменьшается, однако общие закономерности сохраняются. На рис.4, е, ж, з приведены расчетные кривые напряжения, восстанавливающегося на дуговом промежутке при дуговом замыкании в сети с R_N = 134 Ом, С = 1,7× 10^-6 Ф и различных условиях обрыва дуги. Эти кривые получены при начальном U_пр = 4,7кВ и последующих U_пр = 3 кВ. Рис.4, е показывает, что попытка обрыва дуги при первом переходе тока через нуль приводит к непрерывному пробою дугового промежутка, так как бестоковые паузы отсутствуют, и это означает, что погасание дуги после первого перехода тока через нуль в данной сети невозможно. Попытки обрыва дуги при третьем (рис. 4, ж) и пятом (рис. 4, з) переходах тока через нуль приводят к процессам, характерным для перемежающегося замыкания, что указывает на возможность горения и погасания такой дуги.

Сопоставление результатов численного анализа переходных процессов показало, что уменьшение R_N с 227 Ом до 134 Ом не приводит к принципиальному изменению характера горения дуги, а вывод авторов статьи [1], сделанный на основе частных и несовершенных осциллограмм, относится только к этим осциллограммам.

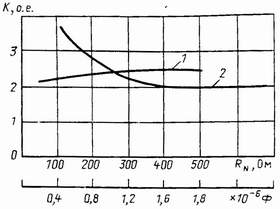
Рисунок 5 - Расчетные зависимости кратности перенапряжения от сопротивления заземляющего резистора и емкости сети: 1-К=f( R_N) при С_о = 1,17× 10^-6 Ф; 2-К=f(С_о) при R_N = 134 Ом

На рис.5 приведены расчетные кривые зависимости максимальной кратности перенапряжения от сопротивления заземляющего резистора при неизменной емкости сети (кривая 1) и от емкости сети при R_N = const (кривая 2). Обе кривые зависимости получены для случая обрыва дуги при третьем переходе тока через нуль. Кривая 1 показывает, что в сети с базовой емкостью С₀ = 1,17× 10^-6 Ф наличие резистора существенно снижает напряжение, но сопротивление резистора в реальном диапазоне слабо влияет на уровень перенапряжений. Кривая 2 отражает известную для сетей с изолированной нейтралью закономерность увеличения перенапряжений с уменьшением емкости сети. В сети с нейтралью, заземленной через резистор с относительно небольшим сопротивлением, следует ожидать нарушения этой закономерности, однако, как видно из кривой 2, этого не происходит. Объясняется это тем, что с уменьшением емкости сети частота свободных составляющих, обуславливающих перенапряжения, увеличивается, и эффект разряда емкостей сети через R_N уменьшается из-за увеличивающегося индуктивного сопротивления обмоток присоединительного трансформатора.

Исследуемая сеть является сетью секции, питающей потребителей собственных нужд энергоблока, и для нее реален ремонтный режим, когда основная часть присоединений отключена и емкость фаз по отношению к земле может уменьшаться в несколько раз. Это означает, что дуговые замыкания в этом режиме при принятом в [1] R_N = 134 Ом могут вызывать перенапряжения, уровень которых может превышать трехкратное значение.

В данной статье не ставилась задача выбора оптимального значения сопротивления в нейтрали конкретной сети, поэтому мы ограничились изложением основных методических предпосылок численного анализа и обосновали достоверность математической модели, что, по нашему мнению, открывает практические возможности для количественной оценки переходных процессов в сетях с нейтралью, заземленной через токоограничивающий резистор. Что касается исследования конкретных сетей, то мы располагаем возможностью оказывать помощь всем заинтересованным сторонам, вплоть до передачи математического обеспечения и консультаций по его освоению.

1. Разработанная математическая модель сети с нейтралью, заземленной через резистор, позволяет проводить достоверный численный анализ дуговых замыканий фазы на землю с целью обоснованного выбора сопротивления резистора.

2. Одной из наиболее характерных особенностей дугового замыкания в сети с нейтралью, заземленной через резистор, является многократный пробой дугового промежутка в виде серий быстро следующих друг за другом пробоев.

3. В сетях с малой емкостью фаз по отношению к земле заземление нейтрали через резистор практически не снижает перенапряжений, так как индуктивное сопротивление обмоток присоединительного трансформатора будет существенно ограничивать отекание зарядов с емкостей сети через заземляющий резистор независимо от его сопротивления.

1. Влияние способа заземления нейтрали сети собственных нужд блока 500 МВт на перенапряжения и работу релейной защиты / В. А. Зильберман, И. М. Эпштейн, Л. С. Петрищев и др. — Электричество, 1987. №12.

2. Серов В. И., Шуцкий В. И., Ягудаев Б. М. Методы и средства борьбы с замыканиями на землю в высоковольтных системах горных предприятий. - М.: Наука, 1985.

3. Дударев Л. Е., Волошек И. В. Выбор сопротивления резистора в нейтрали сетей 6-10 кВ. - Промышленная энергетика, 1989, №6.

4. Дударев Л. Е., Волошек. И. В. Оценка эффективности защиты трансформаторов напряжения от токовых перегрузок. — Электрические станции, 1986, № 11.

"Особенности дуговых замыканий фазы на землю в сетях с нейтралью, заземлённой через резистор" Показать>>

Авторы: Дударев Л.Е. Волошек И.В.

Краткое содержание:В статье рассматриваются вопросы изменения характера дуговых замыканий в зависимости от изменения сопротивления заземляюще- го резистора. Исследования проводятся на математической моде- ли, с помощью которой можно проводить достоверный численный анализ этих замыканий. /"Электрические станции",1992г., №5