| Главная страница ДонНТУ | Страница магистров ДонНТУ | Поисковая система ДонНТУ |
|
|
|
|
|
Отметим несколько особенностей существующих на данный момент методов расчета рекламного бюджета.
По принципу расчета рекламного бюджета все методы можно свести к нескольким основным.
А теперь подробнее.
1. Расчет рекламного бюджета в зависимости от оборота.
В этих методах не без оснований полагается, что увеличение оборота фирмы пропорционально рекламным вливаниям.
Метод определения объема рекламного бюджета в процентах к объему сбыта [2].
В этом методе рекламный бюджет оценивается относительно реально существующего на данный момент оборота: EA = k*S0, где EA - рекламный бюджет (затраты на рекламу); k - сложившийся на рынке (или в самой фирме) показатель отчислений на рекламу относительно объема продаж; S0 - оборот фирмы на момент оценки рекламного бюджета.
Предположим, объем продаж фирмы составляет 500 тыс. долл. Сложившийся на рынке показатель процентного отчисления на рекламу от оборота равен 3%. Тогда рекламный бюджет составит 15 тыс. долл. (0.03? 500).
Пожалуй, единственным достоинством данного метода является его простота. В остальном же этот метод недалеко ушел от принципа оценки рекламного бюджета, что называется “от балды”.
Метод определения объема рекламного бюджета с учетом целей и задач.
Этот метод представлен в [2] и [3]. Формализовать в линейном виде его можно следующим образом: EA = p*n0*S / Smax, где p - стоимость одной, так называемой, рейтинговой единицы; n0 - количество рейтинговых единиц, необходимых для условно 100% охвата целевой аудитории; S - желаемый уровень объема продаж; Smax - максимальный уровень объема продаж (условно 100% охват целевой аудитории).
Допустим, Smax = 100 тыс. долл., n0 = 2000, p = 10 долл. Тогда если фирма ставит целью достигнуть уровня объема продаж 75 тыс. долл., ей необходимо охватить рекламой 75% целевой аудитории (75/100), что потребует оплаты 1500 рейтинговых единиц (2000? 0.75), что в свою очередь потребует 15 тыс. долл. (10? 1500) рекламного бюджета
Модель Юла [4].
Приведем в общем виде формулу для этой модели: EA = p*n0*(1 / k0*k)*(N / Nmax), где p и n0 имеют, по сути, те же значения, что и для метода 2); Nmax - количество потенциальных клиентов фирмы-рекламодателя; N - количество клиентов, которые станут постоянными клиентами данной фирмы; k - отношение количества клиентов данной фирмы, ставших постоянными, к количеству клиентов, которые попробуют товар данной фирмы; k0 - отношение количества клиентов, которые попробуют товар данной фирмы, к количеству увидевших рекламу данной фирмы.
Нетрудно видеть, что N / k - это количество клиентов, попробовавших товар данной фирмы, а N / k*k0 - это количество потенциальных клиентов, увидевших рекламу данной фирмы.
Пусть фирма хочет выйти на рынок с новым видом сигарет. Рынок состоит из 50 млн. курильщиков (Nmax = 50 млн.). Фирма хочет, чтобы на сигареты этой марки переключилось 4 млн. курильщиков (N = 4 млн.). По расчетам маркетологов фирмы это будет составлять 40% от числа попробовавших сигареты данной марки (k = 0.4, соответственно N / k = 10 млн.). Это в свою очередь будет составлять 25% от числа увидевших рекламу данной фирмы (k0 = 0.25, соответственно N / k0*k = 40 млн.). Таким образом, рекламой должно быть охвачено 80% потенциальных клиентов ((1 / k0*k)*(N / Nmax) = 0.8). Условно при охвате 100% потенциальных клиентов необходимо 4000 единиц рекламы (n0 = 4000). Тогда для охвата 80% необходимо 3200 единиц рекламы (n0*(1 / k0*k)*(N / Nmax)= 3200). Одна единица рекламы будет стоить 3 тыс. долл. (p = 3 тыс. долл.). Тогда общий бюджет рекламной кампании должен составить 9600 тыс. долл.
Эта модель практически идентична методу 2) за тем лишь исключением, что вместо величины оборота здесь используется величина количества клиентов, что в ряде случаев (как в случае с сигаретами) является достаточно оправданным.
Модель Видаля-Вольфа [2,4].
Приведем формулу, которая используется в этой модели как базовая: Si = k1*[(Smax - S0) / Smax]*EA - k2*S0, где (Smax - S0) / Smax - изменение уровня объема продаж по сравнению с текущим; k1 - константа реакции оборота на рекламу; Smax - уровень насыщения рынка данным товаром (работой, услугой); S0 - текущий объем продаж; k2 - константа уменьшения объема продаж при отсутствии затрат на рекламу.
В этой формуле уже появился свободный член (k2*S0), который позволяет учесть сокращение оборота при отсутствии затрат на рекламу. Величина Smax аналогична одноименной величине из метода 2). Вычислив отсюда величину EA, получим формулу для расчета величины рекламных затрат: EA = [(S1 + k2*S0) / k1]*[Smax / (Smax - S0)].
Например, фирма имеет оборот 50 тыс. долл. (S0 = 50), через год оборот должен увеличиться еще на 50 тыс. долл. (S’ = 50), уровень насыщения рынка данным товаром составляет 500 тыс. долл. (Smax = 500), k1 = 8, k2 = 0.1. Тогда величина рекламного бюджета EA составит 7639 долл.
Модель ADBUDG [5].
В этом методе в качестве базовой используется следующая формула: ![]() (4.1), где P - доля рынка, которую желает занять фирма; Pmin - доля рынка, которую займет фирма при нулевой рекламе (EA = 0); Pmax - доля рынка, которую займет фирма при наивысшем уровне рекламы (EA® ?); g - коэффициент чувствительности функции реакции; d - коэффициент ослабления.
(4.1), где P - доля рынка, которую желает занять фирма; Pmin - доля рынка, которую займет фирма при нулевой рекламе (EA = 0); Pmax - доля рынка, которую займет фирма при наивысшем уровне рекламы (EA® ?); g - коэффициент чувствительности функции реакции; d - коэффициент ослабления.
Отсюда легко найти величину рекламного бюджета:  .
.
Нетрудно заметить, что величина доли рынка, занимаемой фирмой, есть не что иное, как отношение оборота фирмы к величине уровня насыщения рынка данным товаром (аналогична величине Smax из модели Видаля-Вольфа): P = S / Smax. Тогда формула (4.1) преобразуется в , ![]() где S - желаемый оборот фирмы; Smin - оборот фирмы при нулевой рекламе; Smax - оборот фирмы при наивысшем уровне рекламы.
где S - желаемый оборот фирмы; Smin - оборот фирмы при нулевой рекламе; Smax - оборот фирмы при наивысшем уровне рекламы.
Отметим общие недостатки, характерные для методов расчета рекламного бюджета в зависимости от оборота. Зависимость величины оборота от величины рекламного бюджета имеет либо линейный характер (как в первых 4-х методах), либо нелинейный характер (метод ADBUDG). В этих зависимостях присутствуют от 1-го до 4-х коэффициентов (как линейно зависимых, так и линейно независимых между собой). Чисто с математической точки зрения для нахождения этих коэффициентов необходимо, во-первых, знать количество точек зависимости S = f(EA), равное количеству линейно независимых коэффициентов, а во-вторых, решить систему уравнений относительно этих коэффициентов. Однако если мы можем определить хотя бы одну точку зависимости S = f(EA), тогда непонятно, почему нельзя определить необходимую нам точку. Так, например, для 2-го метода можно было бы непосредственно оценить, что для достижения уровня объема продаж в 75 тыс. долл. необходимо затратить на рекламу 15 тыс. долл. Для модели Юла точно так же можно было бы непосредственно оценить, что для привлечения 4 млн. курильщиков потребуется 9600 тыс. долл. рекламного бюджета. Для остальных методов ситуация аналогичная. Однако, допустим даже, что мы правильно определили величину рекламного бюджета исходя из величины оборота (текущего или желаемого). Но вряд ли есть основания считать, что величина желаемого оборота является оптимальной величиной. Она может быть как завышена (тогда часть рекламных расходов совершаются впустую), так и занижена (тогда при большей величине рекламного бюджета фирма имела бы рентабельность больше, чем получается при данной величине рекламного бюджета).
2.Расчет рекламного бюджета в зависимости от суммы объемов рекламных бюджетов фирм-конкурентов.
В общем случае ![]() (4.2), где EAi - рекламный бюджет i-й фирмы-конкурента; N - количество фирм-конкурентов; k - коэффициент пропорциональности между суммой рекламных бюджетов фирм-конкурентов и рекламным бюджетом данной фирмы.
(4.2), где EAi - рекламный бюджет i-й фирмы-конкурента; N - количество фирм-конкурентов; k - коэффициент пропорциональности между суммой рекламных бюджетов фирм-конкурентов и рекламным бюджетом данной фирмы.
К таким методам можно отнести:
1. Метод оценки рекламного бюджета с учетом практики конкурирующих фирм [4].
В этом методе объем рекламного бюджета рассчитывается как среднее между объемами рекламных бюджетов фирм-конкурентов: 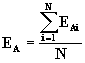 .
.
Надо заметить, что этот метод вряд ли несет хоть какую-либо смысловую нагрузку. Допустим, что на рынке присутствуют две основные фирмы-конкурента. Первая тратит на рекламу 20 тыс. долл., а вторая - 100 тыс. долл. Нетрудно подсчитать, что этот метод дает величину рекламного бюджета 60 тыс. долл., хотя понятно, что все зависит от величины данной фирмы. Если эта фирма по величине сопоставима с первой фирмой, она вряд ли сможет позволить расчетную величину рекламного бюджета без ущерба для оборотных средств. Если же фирма сопоставима со второй фирмой, то для успешной конкуренции она может и должна тратить на рекламу больше расчетной величины.
2. Метод долевого участия на рынке [4].
Этот метод в чистом виде использует формулу (4.2). Здесь k - это доля рынка, которую рассчитывает занять данная фирма. Кроме того, в данном методе необязательно оценивать величины рекламных бюджетов каждой фирмы-конкурента, а достаточно оценить суммарный объем рекламных вливаний по данному товару, работе или услуге.
В данном случае суммарный объем рекламных вливаний по данному товару является величиной внешней для данной фирмы (т.е. определенной). Оценить эту величину можно более или менее точно. Однако гораздо более важно правильно оценить величину доли рынка (k), которую рассчитывает занять данная фирма. Именно от оценки этой величины и зависит, насколько величина рекламного бюджета будет оптимальной. А поскольку данный метод не дает способа оценки этой величины, ценность этого метода весьма сомнительна.
3. Расчет рекламного бюджета по остаточным средствам [4].
Величина рекламного бюджета рассчитывается, исходя из средств, оставшихся после использования на все остальные нужды. Этот метод, по всей видимости, один из самых неудачных, так как низводит рекламную политику до уровня "падчерицы", причем абсолютно несправедливо. Вложения в рекламу ничем не отличаются от любых других вложений. Величина их рентабельности может быть как выше, так и ниже этих других (альтернативных) вложений. Поэтому и рассматриваться затраты на рекламу должны наравне с другими затратами.
4. Расчет рекламного бюджета исходя из критерия оптимальности затрат на рекламу.
Модель Данахера-Руста [6].
В основу данного метода положен алгоритм поиска оптимальной величины рекламного бюджета по критерию максимума отношения эффективности рекламы к затратам на нее. Это, пожалуй, первый метод, перед которым уже можно слегка приподнять шляпу.
В этом методе предполагается, что эффективность рекламы, выражаемая в относительной величине охвата целевой аудитории, зависит от затрат на рекламу следующим образом: f = 4 - EA0 /EA (4.3), где f - значение охвата целевой аудитории (при 100% охвате f = 1); EA - величина затрат на рекламу (величина рекламного бюджета); EA0 - некий коэффициент, по смыслу равный величине затрат на рекламу, при которой эффективность рекламы равна нулю (f = 0). Очевидно, что затраты на рекламу равные EA0 и меньшие этого значения не имеют экономического смысла.
Нетрудно заметить, что 100% охват целевой аудитории (f=1) достигается при бесконечной величине затрат на рекламу (EA® ? ).
Конечно, трудно судить, насколько эта зависимость близка к реальной, тем не менее, она, хоть и примитивно, но по смыслу верно определяет экономическую суть соотношений между величинами охвата целевой аудитории и затрат на рекламу.
Дальше оптимизируется отношение величин охвата целевой аудитории и затрат на рекламу: F = f / EA = 1 / EA - EA0 / EA2 (4.4).
Приравняв производную этой функции по EA нулю и найдя величину EA, получим оптимальную величину затрат на рекламу . Подставив это значение в выражение (4.4), получим максимальное значение отношения величин охвата целевой аудитории и затрат на рекламу и оптимальное значение охвата целевой аудитории fopt = 0.5 (50%). Поскольку в формуле (4.3) присутствует только один коэффициент (EA0), для его определения необходимо найти только одну точку зависимости f(EA). Например, маркетологи фирмы определили, что при затратах на рекламу 25 тыс. долл. (EA = 25) охват целевой аудитории составит 88% (f = 0.88). Из формулы (4.3) нетрудно найти величину коэффициента EA0: =3. Соответственно оптимальная величина затрат на рекламу составит в данном случае 6 тыс. долл.
В оригинале этого метода используется более сложный вариант формулы (4.3): f = 1 - (EA0 / EA)k (4.5), где k - коэффициент, позволяющий, во-первых, учесть скидки на рекламу при увеличении объема, а, во-вторых, более точно учесть падение эффективности рекламы при увеличении объема. С математической же точки зрения, введение дополнительного коэффициента просто позволяет более точно оценить зависимость f(EA) не по одной точке (EA1,f1), как в предыдущем случае, а по двум точкам (EA1,f1) и (EA2,f2).
По сути, все остается прежним, лишь немного меняются оптимальные значения (их нетрудно вычислить в данном случае): EAopt = (1 + k)1/k*EA0 (4.6), Fmax = k / [EA0*(k + 1)1+1/k, fopt = k / (k + 1).
Поскольку в данном случае в исходной формуле используется 2 коэффициента, то для их определения необходимо найти уже не 1, а 2 точки зависимости f(EA), а затем решить нелинейную систему 2-х уравнений: 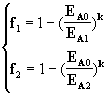 , откуда можно найти коэффициенты k и EA0:
, откуда можно найти коэффициенты k и EA0: 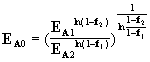 ,
, 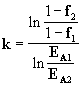 .
.
Например, маркетологи фирмы определили, что при затратах на рекламу 5 тыс. долл. (EA1=5) охват целевой аудитории составит 16% (f1=0.16), а при затратах 25 тыс. долл. (EA2 = 25) - 88% (f2 = 0.88). Подставив эти значения, получим значения коэффициентов EA0 = 4.32, k = 1.21. Из формулы (4.6) находится оптимальное значение величины рекламного бюджета EAopt = 8.34 тыс. долл. Оптимальный охват целевой аудитории составит при этом f = 0.55 (55%).
В оригинале этого метода для характеристики затрат на рекламу используется некая промежуточная величина общих рейтинговых единиц GRPs (Gross Rating Points). Чисто математически это не оправдано, поскольку между затратами на рекламу и количеством GRPs в методе устанавливается достаточно однозначное соответствие.
Теперь необходимо отметить, что функция f(EA), аппроксимирующая зависимость величины охвата целевой аудитории от величины рекламного бюджета, может иметь и другой вид.
Например, эту зависимость можно аппроксимировать функцией ![]() . Здесь так же, как и в формуле (4.5), f® 1 при EA® ? . Значения коэффициентов k и EA0 аналогично находятся решением системы уравнений. Значение же EAopt в данном случае нельзя найти аналитически, что не мешает найти это значение методом подстановки. Для тех же значений f1, f2 и EA1, EA2 значение EAopt = 10.39 тыс. долл. для данного вида аппроксимирующей функции. Оптимальный охват целевой аудитории составит при этом f = 0.46 (46%).
. Здесь так же, как и в формуле (4.5), f® 1 при EA® ? . Значения коэффициентов k и EA0 аналогично находятся решением системы уравнений. Значение же EAopt в данном случае нельзя найти аналитически, что не мешает найти это значение методом подстановки. Для тех же значений f1, f2 и EA1, EA2 значение EAopt = 10.39 тыс. долл. для данного вида аппроксимирующей функции. Оптимальный охват целевой аудитории составит при этом f = 0.46 (46%).
Главная методологическая ошибка данного метода состоит, пожалуй, в том, что в качестве критерия принятия решения выступает максимум отношения величин охвата целевой аудитории и затрат на рекламу. Фактически это отношение эквивалентно рентабельности вложений в рекламу: r = I / EA, где I - прибыль, обусловленная вложениями в рекламу EA, с учетом этих затрат.
Действительно, если считать прибыль I пропорциональной эффективности рекламы f (что не лишено экономического смысла), оптимизация отношения охвата целевой аудитории и затрат на рекламу равносильна оптимизации рентабельности вложений в рекламу. Однако критерием принятия решения о величине рекламных вложений (как, впрочем, и любых других) не может служить оптимальная рентабельность данных вложений. Поясним.
Пусть, например, рекламный модуль в каком-либо издании стоит 1000 руб., а прибыль, принесенная этим рекламным модулем, составит 500 руб. Допустим теперь, что модуль в 2 раза больший по площади стоит 2000 руб., а прибыли он принесет 800 руб. Тогда рентабельность 1-го модуля составит 500/1000=0.5 (50%), а рентабельность 2-го модуля составит 800/2000=0.4 (40%). Если следовать критерию оптимальности, принятому в методе Данахера-Руста, нужно выбрать модуль, меньший по площади. Однако на самом деле все зависит от рентабельности альтернативных вложений. Ведь маленький модуль стоит тысячу рублей. А как можно использовать вторую тысячу рублей? Если рентабельность альтернативных вложений второй тысячи рублей составит величину меньшую 0.3 (<30%), тогда общая прибыль при вложении двух тысяч рублей будет меньше, чем при взятии большего по площади модуля. Например, рекламный модуль в другом издании будет стоить также 1000 руб., однако он принесет 200 руб. прибыли. Тогда общая прибыль составит 500+200=700 руб., что меньше 800 руб., которые получит фирма, если возьмет больший по величине модуль в первом издании.
Из приведенных выше рассуждений можно сделать следующий вывод. Если рекламные вложения самые рентабельные, то рекламный бюджет должен быть не ниже оптимальной величины по методу Данахера-Руста. Далее все зависит от величины альтернативных вложений. Чем менее они рентабельны по сравнению с рентабельностью рекламных вложений, тем больше должна быть величина рекламного бюджета относительно оптимальной величины по методу Данахера-Руста.
Кроме того, считалось, что прибыль I пропорциональна охвату целевой аудитории f. Однако это верно только до определенного значения охвата, выше которого у фирмы может просто не хватать средств (как оборотных, так и основных) для обслуживания такого количества клиентов. Приведем простой пример. Фирма совершает продажи в основном по телефону. Допустим, у фирмы один телефонный номер, и в результате рекламной кампании занятость телефонной линии возросла до 90%. Вся прибыль, которую принесли бы клиенты, которые не дозвонились вследствие занятости телефона, является упущенной прибылью фирмы (вмененными издержками). И в данном случае вложения в дополнительные телефонные линии наверняка окажутся более рентабельными, чем дальнейшие вложения в рекламную кампанию. Это как раз и есть те альтернативные вложения, рентабельность которых необходимо сравнивать с рентабельностью вложений в рекламу. Иначе говоря, у фирмы должно хватать производственных мощностей для возможного увеличения оборота. В противном случае часть рекламных денег может оказаться выброшенными на ветер.
И еще о телефонах. Допустим, что фирма дает рекламу, и телефон, указанный в рекламном объявлении, занят на 25%. Это означает, что из 60 минут он занят в среднем 15 минут. Это, в свою очередь, означает, что из четырех потенциальных клиентов один не дозвонится. Вывод: 25% рекламных денег потеряно. Конечно, такая оценка очень грубая. На самом деле, есть вероятность, что этот клиент позвонит еще раз и с вероятностью 75% дозвонится. Все зависит от готовности потенциального клиента звонить еще и еще раз. В принципе, можно решить задачу оптимизации затрат на коммуникационное обслуживание (телефоны). Однако для грубой оценки можно использовать и вышеприведенное рассуждение. Кстати, проблему занятости телефонов хорошо решают многоканальные телефоны.
|
|
|
|
|