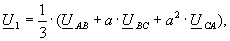 (1)
(1)
О МЕТОДАХ ОПРЕДЕЛЕНИЯ СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ И ТОКОВ ПО РЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ
Сидоренко О. А.
Донецкий национальный технический университет
Кафедра “Электроснабжение промышленных предприятий и городов”
Abstract
Sidorenko O. A. About the methods of definition of symmetric components of currents and voltage on results of measuring. The existent methods of calculation of symmetric components of currents and voltage on the measurers are analysed. Most attention gave to the analytical methods of calculation. More exact and universal formulas are offered, than recommended Intergovermental Standard ГОСТ 13109-97.
С развитием и широким распространением многофазных систем переменного тока появилась потребность в точном описании их несимметричных режимов, весьма многообразных по своей природе. В настоящее время несимметричные режимы становятся не только аварийными, но и рабочими. Сравнительно просто несимметричный режим можно рассчитать с использованием метода симметричных составляющих, к тому же только применение метода симметричных составляющих дает возможность определить токи и напряжения во вращающихся машинах переменного тока, т. е. в таких установках, входные сопротивления которых зависят от порядка чередования фаз питающей сети.
Согласно методу симметричных составляющих линейные симметричные составляющие напряжений и токов определяются:
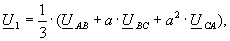 (1)
(1)
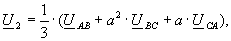 (2)
(2)
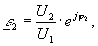 (3)
(3)
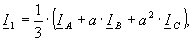 (4)
(4)
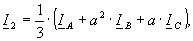 (5)
(5)
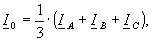 (6)
(6)
где U1, I1 – комплексные напряжение и ток в фазе А линейных симметричных составляющих прямой последовательности; U2, I2 – комплексные напряжение и ток в фазе А линейных симметричных составляющих обратной последовательности; I0 – ток симметричных составляющих нулевой последовательности; UAB, UBC, UCA, IA, IB, IC – комплексные величины линейных напряжений и токов; ε2 – комплексный коэффициент несимметрии напряжения по обратной последовательности; φ2 – аргумент коэффициента несимметрии по обратной последовательности; а – фазный оператор(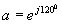 ).
).
Фазные симметричные составляющие напряжений и токов определяются по формулам:
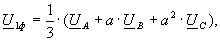 (7)
(7)
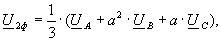 (8)
(8)
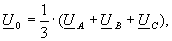 (9)
(9)
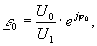 (10)
(10)
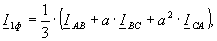 (11)
(11)
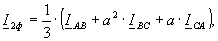 (12)
(12)
где U1ф, I1ф – комплексные напряжение и ток фазных (в фазе А) симметричных составляющих прямой последовательности; U2ф, I2ф – комплексные напряжение и ток фазных (в фазе А) симметричных составляющих обратной последовательности; U0 – напряжение симметричных составляющих нулевой последовательности; UA, UB, UC, IAB, IBC, ICA – фазные напряжения и токи; ε0 – комплексный коэффициент несимметрии напряжения по нулевой последовательности; φ0 – аргумент коэффициента несимметрии по нулевой последовательности.
Отношение модулей линейных симметричных составляющих к фазным составляет 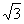 .
.
Вычисление каждой из симметричных составляющих напряжений и токов трехфазной сети в выражениях (1) – (12) предполагает предварительное измерение трех векторов (трех модулей и трех фаз), т. е. шести величин, что представляет существенные затруднения при их измерениях и приводит к большим погрешностям измерения и определения симметричных составляющих.
В практике эксплуатации электрических сетей линейные и фазные напряжения и токи замеряют с помощью вольтметров и амперметров. При этом они имеют вид действительных чисел, а не комплексных, как это предусмотрено в (1) – (12), поэтому целесообразно рассмотреть способы определения симметричных составляющих по результатам измерений в реальных электрических сетях.
Существующие способы определения симметричных составляющих можно разделить на аналитические методы расчета, определение с помощью графических построений, номограмм, таблиц. Аналитические методы расчета делятся на точные, требующие в большинстве случаев использования средств вычислительной техники и приближенные.
К точным аналитическим способам расчета относятся формулы, рекомендуемые в [1]. Так действующие значения напряжений прямой U1 и обратной U2 последовательностей, согласно [1], рекомендуется вычислять по формулам (Б.1) (Б.2), которые можно объединить:
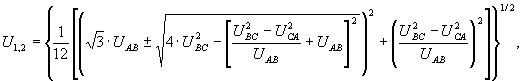 (13)
(13)
где UAB, UBC, UCA – действующие значения междуфазных напряжений.
В [2] показано, что приведенная формула дает точное решение, но область ее применения ограничена: в случае крайней несимметрии при UAB=0 и UBC=UCA дроби в подкоренном выражении дают неопределенность вида
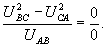 (14)
(14)
Кроме того, формула (13) относится к частному случаю метода симметричных составляющих, когда исходные векторы линейных напряжений образуют замкнутый треугольник, т. е. выполняются условия:
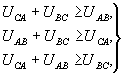
которые необходимо учитывать потому, что на практике возможны неточности в снятии показаний измерительных приборов.
То же касается и расчета действующих значений тока прямой и обратной последовательности по формулам аналогичным (13):
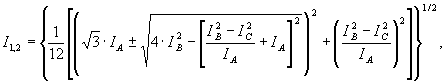 (15)
(15)
где IA, IB, IC – действующие значения фазных токов.
Для определения действующего значения напряжения нулевой последовательности в [1] рекомендуется использовать формулу:
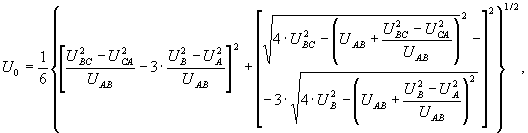 (16)
(16)
где UA, UB, UC – действующие значения фазных напряжений.
При определении U0 в четырехпроводных сетях по (16) при UAB=0 и UBC=UCA (двухфазное короткое замыкание) формула дает неопределенность аналогичную (14) и, таким образом, неприменима при крайних случаях несимметрии. Кроме того, формула (16) отличается громоздкостью, что затрудняет использование ее в практических целях.
Следует заметить, что официальное издание [1] Госстандарта Украины (1999 г.) имеет в формуле для определения U0 (формула (Б.23) в [1]) опечатку: неверно указан знак.
В [1] приведены формулы для задач, где требуется только вычисление модулей симметричных составляющих и коэффициентов несимметрии, но нет выражений для определения фазовых углов φ2 и φ0.
В [3] даны выражения для определения симметричных составляющих, предполагающие измерение абсолютных значений трех, а для определения составляющей нулевой последовательности – шести (трех линейных и трех фазных) напряжений:
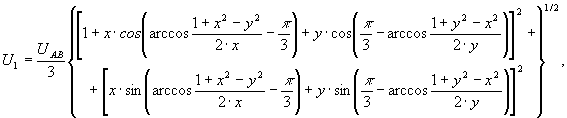 (17)
(17)
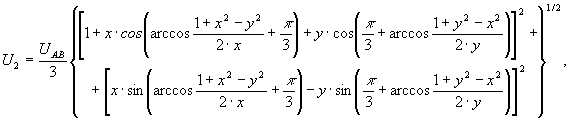 (18)
(18)
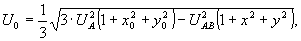 (19)
(19)
где
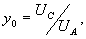
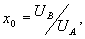
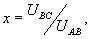
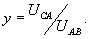 (20)
(20)
Здесь же предложены формулы для определения фазных углов векторов напряжений прямой (φ’АВ) и обратной (φ”АВ) последовательностей относительно вектора напряжения в фазе АВ (обозначения по[3]):
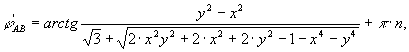 (21)
(21)
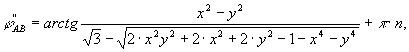 (22)
(22)
где n устанавливают по знаку числителя и знаменателя выражений (21) – (22).
Как видно из (17) – (22), в случае равенства какого-либо из линейных напряжений нулю (для U0, φ’АВ, φ”АВ – UAB=0) формулы дают деление на нуль, а следовательно, ограничены в использовании. Кроме того, (17) – (20), (21), (22) представляют собой сложные математические выражения и требуют значительных вычислений.
Согласно [4], алгоритмом обладающим наивысшей точностью расчета (с методической погрешностью Δм=0) симметричных составляющих U1 и U2 основывается на соотношениях треугольника. Он был рекомендован в [5]. При получении выражений [5], за действительную ось был принят вектор UAB, относительно которого определялись и фазы векторов U1 и U2.
Вместе с тем, алгоритм [5] трудно использовать для быстрой оценки значений U1 и U2 (он содержит 19 арифметических операций и две операции извлечения квадратного корня), поэтому в [4] сделано его аналитическое упрощение за счет того, что действительную ось направлено по вектору прямой последовательности. В этом случае связь линейных напряжений с напряжениями U1 и U2 выражается системой уравнений
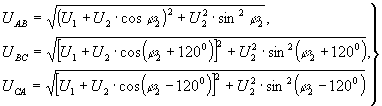 (23)
(23)
решение которой, после дальнейших упрощений, сделанных в [6], приводит к результату:
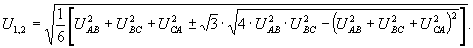 (24)
(24)
Как показали расчеты, формулы (24) дают во всех случаях точные решения, не имеют ограничений области применения как формулы (13), (17), (18) и более просты в вычислениях, чем выражения из [1].
С учетом известного соотношения модулей линейных и фазных симметричных составляющих из (24) можно вывести выражения для фазных симметричных составляющих, которые были получены и в работе [7]:
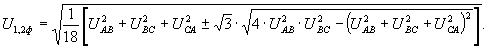
Подобные формулы могут быть также использованы для определения линейных и фазных симметричных составляющих токов аналогично с (15):
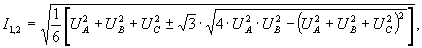
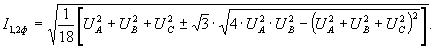
На основании известных соотношений метода симметричных составляющих
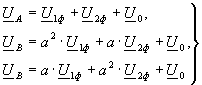 (25)
(25)
и формул (7) – (9) вычисление симметричной составляющей напряжения нулевой последовательности может быть произведено по формуле
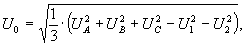
которая с учетом (24) принимает вид:
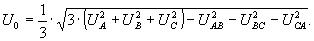 (26)
(26)
Формула (26) при расчетах дала во всех случаях точные результаты, не имеет ограничений области применения как (16), (19) и имеет более простой вид, чем формула из [1].
На основании (26) формула для определения симметричной составляющей тока нулевой последовательности будет представлять собой выражение:
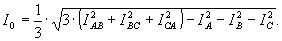
В работе [8] дано выражение для точного аналитического определения аргумента коэффициента несимметрии по обратной последовательности <φ2, которое после некоторых преобразований можно выразить через исходные значения линейных напряжений:
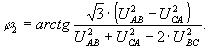 (27)
(27)
Если знаменатель (27) меньше нуля, то к углу φ2, определенному по (27), надо прибавить 1800.
Рассчитывать φ2 можно также по выражению из [4], получаемое решением системы (23), но при этом надо заметить, что там допущена ошибка - в числителе должно быть: UCB2 -UAC 2.
Для определения аргумента коэффициента несимметрии по нулевой последовательности для системы фазных векторов, содержащих только прямую и нулевую последовательность (UAB=UBC=UCA), в [5] приводится сравнительно простая, дающая однозначные результаты, формула:
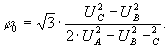 (28)
(28)
При вычислениях по (28) нужно учитывать, что если знаменатель меньше нуля, то к углу φ0, определенному по (28), надо прибавить 1800.
Наибольшую сложность представляет определение φ0 для системы фазных векторов, содержащих прямую, обратную и нулевую последовательности. В [4] с этой целью дается рекомендация, что систему фазных напряжений необходимо привести к виду, в котором напряжение U2 отсутствует (даны приближенные формулы для корректировки), а затем вычислять по (28). Но, как показали расчеты, такая методика не дает правильных результатов.
В [9] приведена формула для определения φ0, который выражен через модули величин, входящих в первое уравнение системы (25). Решение находится в виде корней квадратного уравнения:
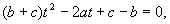 (29)
(29)
где
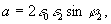
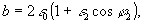
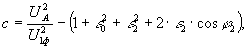
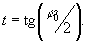
На основании проверочных расчетов по формулам, приведенным в [8], решение (29) – выражение для определения φ0 нужно записать в несколько ином виде, чем оно приведено в [8]:
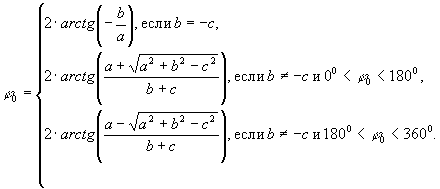 (30)
(30)
Как видно из (30), φ0< определяется неоднозначно. Для уточнения значения φ0 в [8] рекомендуется подставить полученные значения в уравнения для определения модулей напряжений UB и UC через симметричные составляющие (втрое и третье уравнения системы (25)). Значение φ0, при котором модуль фазного напряжения, вычисленного по этим формулам, совпадает с исходным, будет истинным.
Запись уравнения для определения φ0 в форме (30) дает возможность более быстрого определения φ0, если заранее приближенно известно в каких пределах лежит φ0, кроме того, в (30) устранена неточность [8]. Там рекомендуется еще учитывать свойства тангенса угла (что увеличивает объем вычислений), а это делать не нужно, так как решение получено из квадратного уравнения.
По выражениям напряжений (27), (28), (30) для определения фазовых углов φ2 и φ0 для напряжений возможно вычислять аналогичные углы для токов. При этом в указанных формулах вместо значений линейных и фазных напряжений нужно учитывать линейные и фазные токи (как это сделано в выражения для определения I1, I2, I0).
Для быстрой оценки U1, U2, U0 в [1] допускается использовать и приближенные формулы:
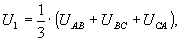 (31)
(31)
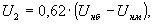 (32)
(32)
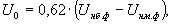 (33)
(33)
где Uнб (Uнб.ф), Uнм (Uнм.ф) – наибольшее и наименьшее действующие значения из трех междуфазных (фазных) напряжений.
В отличие от точных формул определение симметричных составляющих токов по (32) и (33) – недопустимо, так как I2 и I0 могут достигать значительных величин, а данные формулы основаны на допущениях: U2<<U1 и U0<<U1, которые обычно выполняются в сетях электроснабжения.
В [4] предложена приближенная формула для оценки φ2, также основанная на том, что U2<<U1:
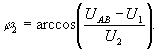 (17)
(17)
Если UCA<UAC, то знак угла, определенного по (34), необходимо изменить на противоположный.
Величиной φ0 в большинстве практических расчетов пренебрегают или принимают φ0 » - φ2 [9].
Неоднократно предпринимались попытки упростить определение симметричных составляющих с помощью графический построений [10, 11], номограмм [3, 12], таблиц [3].
Геометрические построения позволяют четко определить расчетные формулы, но требуют значительных затрат времени.
Номограммы, несмотря на малую точность, определяемую одним-двумя знаками, играют весьма важную роль при анализе несимметричных процессов, определении максимальных значений линейных и фазных напряжений и токов, качественной оценке несбалансированных процессов, при предсказании динамики многофазных систем в аварийных режимах, расчетах коротких замыканий.
Несмотря на простоту и достаточную точность, таблицы и номограммы не удобно использовать при обработке большого количества данных измерений.
Вывод
В связи с доступностью средств вычислительной техники при обработке большого количества информации, что связано с контролем качества электроэнергии, предпочтительны точные аналитические методы определения симметричных составляющих. Расчет симметричных составляющих напряжений наиболее целесообразно вести по формулам (24), (26) – (28), (30), которые имеют преимущества перед формулами, рекомендуемыми ГОСТ 13109-97: более универсальны, дают возможность определения комплексных значений, проще в вычислении. Предложенные выражения пригодны для вычисления комплексных значений симметричных составляющих токов.
Литература
1. ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. Введен в Украине с 01.01.2000.
2. Лютий О. П. Методи оцінювання параметрів несиметрії і несинусоїдальності режимів у системах електропостачання з різкозмінним навантаженням. Автореферат дисертації на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.14.02. – Інститут електродинаміки Національної Академії наук України, Київ, 2003. – 19 с.
3. Шидловский А. К., Музыченко А. Д. Таблицы симметричных составляющих. – К.: Наукова думка, 1976. – 204 с.
4. Железко Ю. С., Артемьев А. В. Определение симметричных составляющих напряжений с помощью вольтметра. – Известия вузов. Энергетика, 1985, №2. – С. 10 – 15.
5. Инструктивные материалы Главгосэнергонадзора. – М.: Энергоатомиздат, 1983. – 400 с.
6. Цапенко Е. Ф., Юнис Камаль. Контроль симметричных составляющих линейных напряжений сетей 6-10 кВ. – Известия вузов. Энергетика, 1991, №5. – С. 47 – 50.
7. Цапенко Е. Ф., Юнис Камаль. К вопросу расчета симметричных составляющих фазных напряжений электрических сетей. – Известия вузов, 1992, №2. – С. 31 – 33.
8. Кузнецов В. Г., Каплычный Н. Н., Третьяк В. Т. Определение коэффициентов несимметрии и неуравновешенности в трехфазных сетях с нулевым проводом. – Проблемы технической электродинамики, 1975, вып. 53. – С. 85 - 89.
9. Левин М. С., Лещинская Т. Б. Анализ несимметричных режимов сельских сетей 0,38 кВ. – Электричество, 1999, №5. – С. 18 – 22.
10. Рожавский С. М. Номограмма для расчета режима несимметрично нагруженной трехфазной линии с изолированной нейтралью. – Известия вузов. Энергетика, 1965, №6. – С. 93 – 94.
11. Цицикян Г. Н., Зайцев Г. З. Об оценке несимметрии напряжений в трехфазных системах электроснабжения. – Электричество, 1999, №5. – С. 13 – 17.
12. Ковзан А. А. Оценка несимметрии в трехфазных системах с помощью номограмм. – Известия вузов. Энергетика, 1961, №7. – С. 28 – 34.