Автоматизированное проектирование микропрограмных автоматов Мура с преобразованием кодов объектов в базисе FPGA

Автореферат магистерской работы

Руководитель: д. т. н. Баркалов А. А.

Автор: Боровлев А. С.

Введение

Целью данной научно-исследовательской работы является разработка программы для создания VHDL-модели цифрового автомата Мура. Выбор этой задачи был обусловлен тем, что все современные программы моделирования не выполняют условий оптимизации, необходимых при разработке цифрового автомата. То есть, при использовании, например, языка VHDL возможно описать автомат Мура, но не существует возможности сделать это описание универсальным, пригодным для моделирования автомата Мура с более сложной (или более простой) структурой. В любом случае этот код будет очень громоздким и неудобным для изменения.

В этой научно-исследовательской работе разработанная программа, которая на основании специального языка описания ГСА, строит оптимизированную VHDL-модель автомата Мура.

1. Введение в цифровые автоматы

Принцип микропрограммного управления был предложен в 1951 г. М. Уилксом и предполагает наличие в любой цифровой системе устройства управления (УУ), которое координирует все блоки системы. Исполнительная часть системы, которая выполняет обработку данных, называется операционным автоматом (ОА), а цифровая система в целому называется операционным устройством. Алгоритм работы системы задается одним из формальных методов, на практике инженерного проектирования наиболее широко используется язык граф-схем алгоритмов (ГСА).

В операционных вершинах ГСА записываются наборы микроопераций Yt, где Y={y1,...,yn} – множество микроопераций, которые инициируют заданный вид обработки данных в ОА.

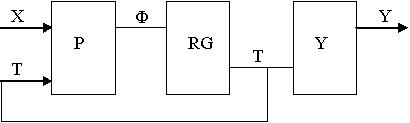
В условных вершинах ГСА записываются логические условия Xt, где X = {x1,...,xL} – множество исходных сигналов ОА, которые идентифицируют состояние процесса обработки информации. Структура операционного устройства приведена на рис. 1.1.

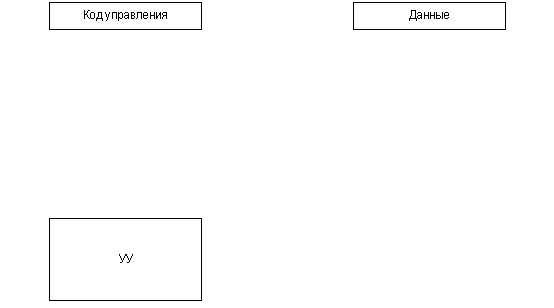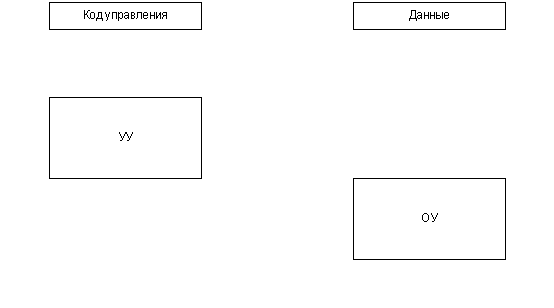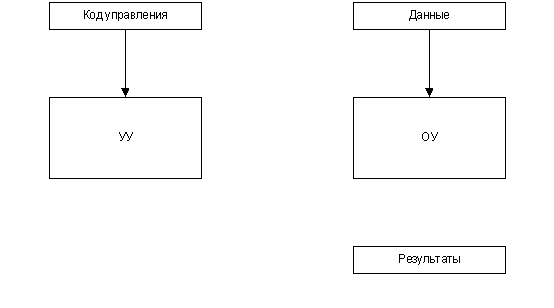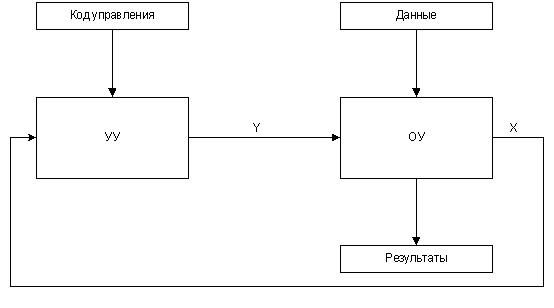
Рисунок 1.1. Структурная схема операционного устройства (анимированный рисунок)

Алгоритм управления системой задается кодом управления, которое поступает в УУ из внешней среды. Алгоритм управления ОА называется микропрограммой, откуда и пошло название принципа М. Уилкса.

Итак, мы имеем схему, которая состоит из двух независимых устройств. Мы можем заменять как УУ так и ОА не разрушая трудоспособности системы, при условиях сохранения протокола взаимодействия (сигналы могут иметь другое значеня, но их количество должна сохраняться). Например, есть возможность использовать одно и то же управляющее устройство для разных процессов (при условии сходности алгоритма работы), или заменить его на другое (при изменении условий протекания технологического процесса).

2. Методика синтеза управляющих устройств

2.1 Общая структура управляющего устройства

В связи с тем, что управляющее устройство представляет собой "черный" ящик, на вход которого подают какие-то логические условия (вектор - Х), а на выходе получают управляющие сигналы (вектор - Y), то работу такого устройства можно представить как:

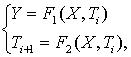(2.1)

где Y - управляющие сигналы, X - логические условия, Ti - текущее состояние устройства, Ti+1 - следующее состояние устройства.

Формулу (2.1) не надо путать с внутренней организацией устройств, это лишь общая математическая модель описания их поведения.

Из формулы (2.1), мы видим, что для построения управляющего устройства нам необходимо найти функции формирования вектора Y - F1, и перехода в следующее состояние - F2. Методика реализации этих функций, а так же и методика синтеза, зависит от типа управляющего устройства. На текущий момент существует три группы таких устройств: устройства с жесткой логикой; устройства с программируемой логикой и композиционные.

2.2. Устройства с жесткой логикой

Реализация микропрограммы в виде сети элементов "И", "ИЛИ", "НЕ", которая связанна с регистром памяти RG, порождает автомат с жесткой логикой или микропрограммный автомат. Сеть элементов называется комбинационной схемой (КС).

Для формирования распределенной по времени последовательности наборов микроопераций Y(0), Y(1), ..., Y(t), где t – время, необходимо располагать информацией о предыдущей работе системы. Эту информацию представляют собой наборы логических условий X(0), X(1), ..., X(t-1), которые поступают на вход МПА в предыдущие моменты времени. Таким образом,

Y(t) = f(X(0), X(1), …, X(t-1), X(t))

(2.2)

2.2.1. Устройство Мура.

Данное устройство работает по следующей формуле:

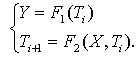(2.2.1)

Функции вида (2.2) очень громоздкие и их практически нельзя реализовать аппаратно, в особенности при наличии циклов с неизвестным количеством повторений.

Для задачи момента изменения кодов состояний (переключения) автомату применяется сигналы синхронизации Clock.

Рассмотрим типы устройств более детально.

Как видно, вектор исходных переменных Y зависит лишь от текущего состояния автомата. Это приводит к тому, что мы различаем переходы автомата от формирования исходных функций. Это приводит к уменьшению формул формирования исходных сигналов, но в многих случаях увеличивает количество положений автомата, который приводит к увеличению элементов памяти и формул перехода. По этой причине классический автомат Мура не используется.

2.3. Устройство с программируемой логикой

В отличие от устройств с жесткой логикой данный тип устройств сохраняет информацию об адресе перехода и исходные функции в специальной схеме – ПЗУ. Текущее состояние автомата сохраняется в регистре и представляет собой адрес ячейки ПЗУ из которой достается информация о функциях управления Y, а также адрес следующей ячейки ПЗУ. Видно, что эти автоматы, как и автомат Мура, формируют исходные переменные лишь в зависимости от текущего состояния, а логические условие используются для формирования следующего адреса в ПЗУ. За один такт автомата может быть обработана одна операционная и/или условная вершина, что приводит к низкому быстродействию данных типов устройств. Их преимущество состоит в том, что ГСА практически не требует дополнительной обработки и формирование таблицы переходов автомата и на основе алгоритма может записано содержание ПЗУ. Также микросхема ПЗУ на порядок дешевле FPGA или микросхем комбинационной логики.

2.4 Композиционное микропрограммное устройство управления

Данный тип устройств объединяет в себе преимущества двух предыдущих типов. Граф-схема алгоритма разбивается на операторные линейные цепи, коды операторных вершин в середине цепи нумеруются последовательно (то есть каждая следующая вершина имеет код на единицу больше предыдущей). Для перехода от вершины к вершине в середине цепи достаточно счетчика, который уменьшает общий размер КЛС автомата. Для переходов между цепями используется КЛС, но за счет того, что цепей, обычно, меньше, чем вершин, она меньше, чем в эквивалентном автомате Мили/Мура. Исходные функции формируются с помощью ПЗУ.

3. Синтез логической схемы автомата Мура

Логическая схема автомата МПА Мура задается системой булевых функций

Ф = Ф (Т, Х),	(3.1)
Y = Y (T),	(3.2)

т.о. исходные сигналы Y зависят только от состояний автомата. Фактически, коды состояний K(am) представляют собой коды микроопераций, которые записаны в операторних вершинах, отмеченных состояниями. Это порождает структуру логической схемы автомата Мура (рис. 3.1), что содержит Р-подсхему для реализации (3.1) и Y-подсхему для реализации (3.2).

Рис. 3.1. Структурная схема автомата Мура

Как видно из рис. 3.1., в простейшем случае автомат Мура представляется двухуровневой структурой, у которой система (3.1) реализуется на ПЛМ или ПМЛ, а система (3.2) - на ППЗУ. Основой для синтеза схемы автомата Мура S по ГСА Г (рис. 3.2). Как видно из (3.2) каждая операторная вершина ГСА отмечается отдельным состоянием. Это приводит к тому, что в автомате Мура обычно имеется больше состояний, чем в эквивалентном автомате Мили. Так, в автомате Мура A={a1,...,a7}, а в эквивалентном автомате Мили A={a1,a2,a3}.

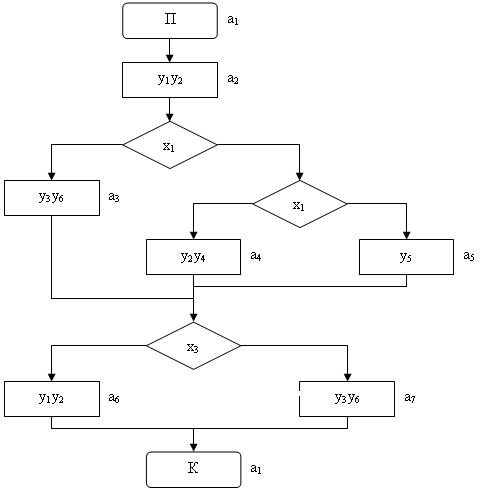
Рис. 3.2. Начальная ГСА Г

Построив таблицы ПСТ (прямая структурная таблица) и таблицу микроопераций МПА, получим следующую функциональную схему:

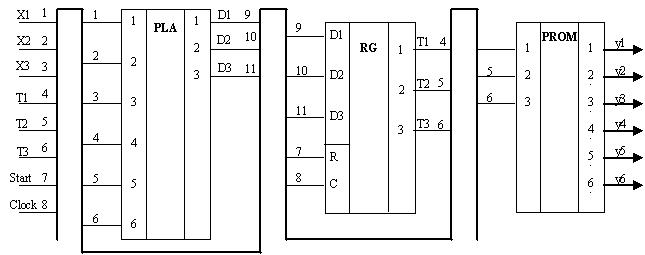
Рис. 3.3. Функциональная схема автомата Мура S

К недостаткам автомата Мура относятся:

количество состояний эквивалентного автомата Мили меньше, чем количество состояний автомата Мура;
количество входов Р - подсхемы и регистра памяти для автомата Мили меньше, чем для эквивалентного автомата Мура;
количество срок ПСТ автомата Мили меньше, чем у эквивалентного автомата Мура.

Несмотря на все недостатки автомата Мура в сравнении с автоматом Мили, автомат Мура имеет важный перевес - ДНФ системы (3.2) проще, чем ДНФ микроопераций автомата Мили.

Разработка универсального языка для программы моделирования автомата Мура

Для программы моделирования был разработанный язык описания ГСА. Во время работы программа анализирует этот код и, на его основе, строит модель. Разработанный язык легок для понимания, поэтому он может быть использован как с целью разработки, так и в учебных целях. Рассмотрим его детальнее.

Общие положения

каждая строка языка заканчивается символом ".". Вся строка после точки рассматривается как комментарий пользователя;
описание ГСА всегда начинается вершиной "НАЧАЛО" и заканчивается вершиной "КОНЕЦ";
в одном файле может быть представлена только одна ГСА;
в одной ГСА может быть только одна вершина "НАЧАЛО" и одна вершина "КОНЕЦ";
файл состоит из двух частей. Первая - описание переходов, вторая - описание операторных вершин;
большие и маленькие буквы не различаются;
номера вершин - целые положительные числа;
допускается использования только латинских букв (не распространяется на комментарии);
пустые строки игнорируются;
порядок прохождения вершин может быть произвольным, поскольку произвольной может быть их нумерация в границах ГСА;
в каждом строке допускается описание только одной вершины на-бора микроопераций;
если в нескольких операторных вершинах содержатся одинаковые наборы микроопераций, они могут быть описаны или одним набором, или несколькими наборами с одинаковым содержанием.

Описание вершин:

вершина "НАЧАЛО": ‹№ вершины›"S":"№ следующей вершины".;
вершина "КОНЕЦ": ‹№ вершины›"E".;
операторная вершина: ‹№ вершины›"O":"Yn","№ следующей вершины"., где Yn - набор микроинструкций, которая выполняется в текущей операторной вершине;
условная вершина: ‹№ вершины›"O":"Xn","переход по 1","переход по 0"., где Xn - условие, которое проверяется;
комментарий (действует от символа ";" до конца строки): ;[текст_комментария]

Описание наборов микроинструкций: "Yn": ‹список микроинструкций›

Таким образом, мы получили целиком простой для понимания и изучение универсальный язык. Рассмотрим использование разработанного языка на примере реальной ГСА (рис. 1).

Как видно из приведенного рисунка, все вершины, включая начальную и конечную, нумеруются, причем конечная нумеруется последней, а начальная первой. Кроме того, набор микроопераций каждой операторной вершины нумеруется в отдельности.

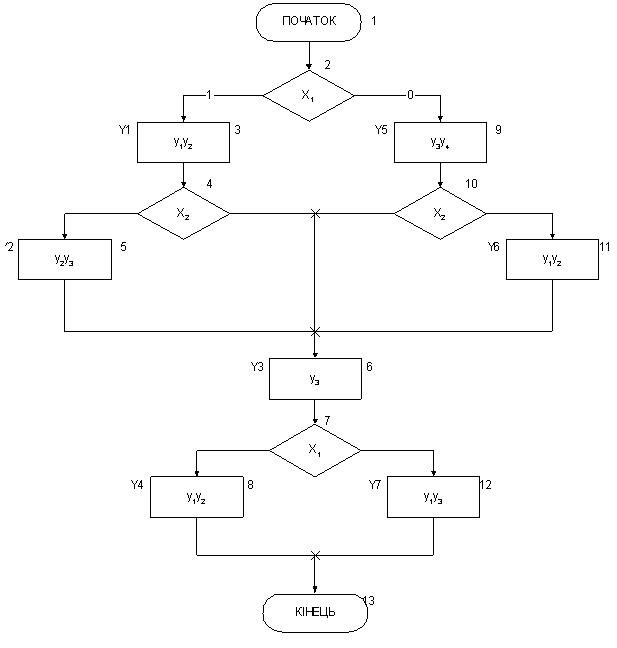
Рис. 1. Пример ГСА

Используя язык описания, приведеный выше, мы получаем следующее описание ГСА:
1S:2.
2x:x1,3,9.
3O:Y1,4.
4X:X2, 5,6.
5O:y2, 6.
6o:y3,7.
7X:x1,8,12.
8o:y1,13.
9O:y4,10.
10x:x2,6,11.
11O:y1,6.
12o:y5,13.
13e.

Y1:y1,y2.
Y2:y2,y3.
Y3:y3.
Y4:y3,y4.
Y4:y1,y3.

Заключение

На данном этапе работы мы получили универсальный язык описания ГСА для автоматов Мура. Язык, как было сказано выше, прост для изучения и может быть применен в обучающих целях. В дальнейшем будет произведена разработка программы, которая на основании языка разработанного языка будет строить работоспособную VHDL-модель автомата Мура.

Список литературы

А. А. Баркалов "Синтез устройств управления на программируемых логических устройствах" — Донецк: ДонНТУ, 2002
Соловьев В.В. Проектирование функциональных узлов цифровых систем на программируемых логических устройствах. — Минск: Бестпринт, 1996
Mano M. Computer System Architecture. — N.D.: Prentice Hall, 1997
Угрюмов Е.П. Цифровая схемотехника — Сб.: БХВ — Петербург, 2000