Авторы: А.С. Холодов, А.И. Лобанов, А.В. Евдокимов

А.С. Холодов, А.И. Лобанов, А.В. Евдокимов

РАЗНОСТНЫЕ СХЕМЫ ДЛЯ РЕШЕНИЯ ЖЕСТКИХ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ПРОСТРАНСТВЕ
НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ

Предисловие

Данная книга написана на основе конспекта односеместрового курса лекций, под несколько иным названием читаемого на факультетах управления и прикладной математики (ФУПМ) и аэрофизики и космических исследований (ФАКИ) Московского физико-технического института (на ФУПМ с 1985 года). Лекции поддерживаются лабораторным практикумом из 8 работ по соответствующим разделам курса. В общем “вычислительном” образовании студентов ФУПМ эти лекции стоят между вводным курсом вычислительной математики (в объеме книг [1,2]) и фундаментальным курсом теории разностных схем (в объеме книги [3]). Это обстоятельство, а также естественное желание возможно большего охвата идей и конкретных разностных схем из всего огромного числа разработанных к настоящему времени, определило содержание и характер изложения материала данного курса.

В качестве основного подхода к построению разностных схем для простейших (модельных) уравнений принят известный метод неопределенных коэффициентов (позволяющий рассматривать достаточно обширные семейства схем), дополненный анализом этих семейств в пространстве неопределенных коэффициентов. Анализ разностных схем в пространстве коэффициентов (предложенный в [4]) оказался достаточно универсальным и весьма конструктивным средством не только для качественного сравнения различных схем (типа: устойчива – неустойчива, монотонна – немонотонна, первого – второго порядка аппроксимации и т.п.) но, в определенном смысле, и количественного их сопоставления (например, в смысле “расстояния” между схемами в пространстве неопределенных коэффициентов, если принять достаточно естественную гипотезу о том, что близкие в таком пространстве схемы близки и по своим свойствам).

Поскольку курс в целом ориентирован на методы решения нелинейных дифференциальных уравнений, характерной чертой которых являются разрывные решения, области больших градиентов (“пограничные слои”) и т.п., достаточно большое внимание уделено построению монотонных (мажорантных) схем. При переходе от модельных уравнений к линейным системам и нелинейным уравнениям в курсе активно используются характеристические свойства уравнений гиперболического типа и аналогичные методы расщепления для других типов уравнений, интегро-интерполяционный метод (метод интегрального тождества) и другие эффективные способы обобщения схем с сохранением заложенных в модельные схемы свойств.

• Численное интегрирование жестких систем обыкновенных дифференциальных уравнений (ОДУ)

• Жесткие ОДУ

• Линейные однородные уравнения первого порядка

Рассмотрим вначале простейшее уравнение

(1)

на отрезке

(2)

и задачу Коши для (1)

u(0) = u 0 (3)

Решение (1)-(3), очевидно,

(4)

Если , имеем неограниченное (неустойчивое) решение (рис. 1 .1).

В этом случае нет ничего, что могло бы в аналогичных, но более сложных случаях (нелинейные системы) облегчить жизнь вычислителю. Надо интегрировать (1) с шагом по времени, обеспечивающим необходимую точность до тех пор, пока это возможно. Если , то решение задачи (1)-(3) ограниченное ( ). С точки зрения вычислителя важна величина отрезка интегрирования T . Если , то имеем обычную ситуацию (рис. 1 .2), можно пользоваться стандартными методами численного интегрирования (Эйлера, Эйлера–Коши, Рунге–Кутты, Адамса и т.д.). Если , то имеем решение типа “пограничного слоя” (рис. 1 .3) с резким изменением u на малом (в масштабе T ) отрезке [0,T 0 ] . В аналогичных, но более сложных ситуациях (когда положение “пограничного слоя” заранее неизвестно и т.д.) при численном интегрировании возникают осложнения, которые и будут рассмотрены позднее. Основная идея заключается в том, чтобы численный метод обеспечивал качественно правильное поведение численного решения на участке “пограничного слоя” (при ), т.е. быстрое затухание, и возможно точнее воспроизводил решение на основном участке интегрирования (вне “пограничного слоя”).

• Системы линейных однородных уравнений

Пусть имеется J уравнений (1)

j = 1,…,J (5)

с начальными условиями .

Если обозначить

,

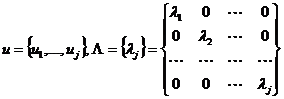и перейти к векторной форме

, (6)

то, сделав замену , где

,

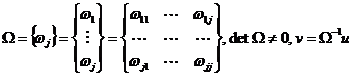т.е. полагая , получим вместо (6) однородную линейную систему ОДУ

. (7)

Так как , то или .

Наоборот, если задана система (7), то умножая ее скалярно J раз на левые собственные векторы матрицы A , определяемые, как это следует из (7), с точностью до их длины, из J линейных однородных систем

или (8)

приходим к эквивалентной (7) совокупности уравнений (5), связанных друг с другом только через начальные условия

v(0) = v 0 или . (9)

Здесь – собственные значения матрицы A , т.е. корни характеристического уравнения

, (10)

– многочлен степени J .

Решение каждого из уравнений (5) имеет вид (4), т.е. , а значит, решение задачи Коши (7),(9) есть , т.е. является линейной комбинацией экспонент (если все действительны) или имеет более сложный характер с присутствием гармонических составляющих (если среди будут комплексно-сопряженные корни уравнения (10)).

• Пример: задача Коши для линейного однородного уравнения второго порядка

, ,

( , a, b – константы). Обозначим и введем вектор , тогда

,

или, в векторной форме,

, ,

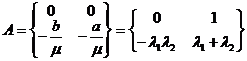где – собственные значения матрицы A из (10):

,

.

При |a|~|b|~1 , приближенно имеем , ; , . Далее, из (8)

, ,

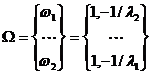при .

Тогда, учитывая, что , получаем:

,

.

Если оба действительны, то имеем комбинацию двух экспонент, затухающих при ? 1 <0 и ? 2 <0. Если ? 1 = ? + i ? , ? 2 = ? – i ? , то u ( t ) = e ?t {[( u 1 – ?u 0 ) sin ( ?t )]/ ? + u 0 cos ( ?t )} , и на экспоненту e ?t накладываются гармонические колебания с периодом T * ~1/ ? , т.е. характер поведения решения определяется собственными значениями матрицы A .

В общем случае можно выделить следующие четыре характерных ситуации:

Случай А не доставляет вычислителю никаких хлопот, проходят стандартные методы (явные схемы Рунге–Кутты, Адамса т.п.), уже изучавшиеся в курсе вычислительной математики.

Случай Б практически безнадежен (неустойчивые по Ляпунову системы ОДУ).

Случай В довольно часто встречается на практике и для него, в принципе, есть специальные методы, основанные на осреднении быстроосциллирующих гармоник (методы осреднения и т.п.).

Случай Г мы и будем рассматривать (жесткие системы ОДУ). Для матрицы A большой размерности найти все собственные числа (полная спектральная задача) не очень просто из-за ее плохой обусловленности. Действительно, для жесткой системы число обусловленности матрицы A

(11)

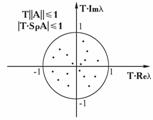
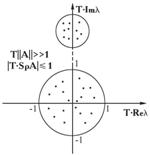
или, приближенно, || A ||Т >>1, и отсюда идут все неприятности. Здесь и в дальнейшем || · || – норма матрицы.

• Нелинейные жесткие уравнения

Рассмотрим одно сингулярно возмущенное уравнение , ,

, , (12)

В случае если предельное (вырожденное) уравнение (12) при

при каждом значении t имеет единственное решение

, (13)

и в окрестности этого предельного решения , (условие устойчивости решений (12)), имеем ситуацию, изображенную на рис. 1 .5. Аналогичная ситуация была и в примере 1.1.3 при малых (в том случае предельное уравнение было ). Как и в линейном случае, поведение решения разделяется на два характерных участка: пограничный слой для малых (его длина ), и близкое к предельному решению (13) поведение при . Обычно определяемый “физикой задачи” участок интегрирования .

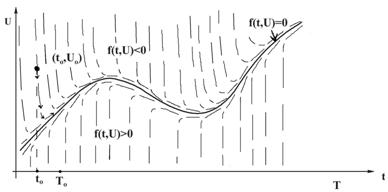
Рис. 1 .5. Поле решений уравнения (12)

• Пример: сингулярно возмущенная нелинейная система второго порядка

Рассмотрим следующую автономную (правая часть не зависит от времени) систему двух нелинейных уравнений:

, , , , ,

, . (14)

Убедимся, что система жесткая. Записав (14) в векторной форме u={x,y} , , , 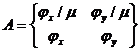имеем:

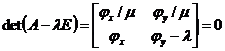или

.

Если мало, то , . Видно, что , при , поэтому ? 2 называют нормальной частью спектра, а ? 1 – жесткой частью спектра.

Предельное уравнение:

или ,

, . (15)

В случае уравнения Ван дер Поля

; (16)

(которое важно во многих приложениях, например, в радиотехнике), получаем предельное уравнение и поле решений в фазовой плоскости, изображённое на рис. 1 .6.

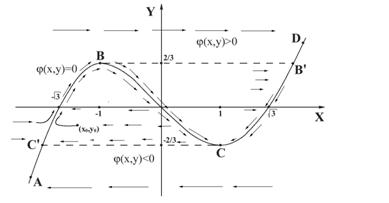
Рис. 1 .6. Поле решений уравнения Ван дер Поля

Вдали от линии имеем почти горизонтальное поле направлений , на самой линии выделяются две устойчивые ветви AB и CD и одна неустойчивая ветвь BC . При любых начальных значениях траектория этой системы – замкнутая кривая BB?CC? .

1) На участке траектория почти горизонтальна и приближенно определяется уравнениями:

, , (17)

(пограничный слой).

2) При и система описывается предельными уравнениями (16) (квазистационарный режим вплоть до точки B ). Если и после т. B пользоваться предельными уравнениями (16), то мы бы двигались по BC . Но реальная система на этом участке неустойчива и система сходит с этой ветви на ветвь DB?C . На этом участке и решение определяется поведением .

3) Опять пограничный слой (17) при , за ним квазистационарное движение на участке B?C при , пограничный слой и т.д. (все повторяется).

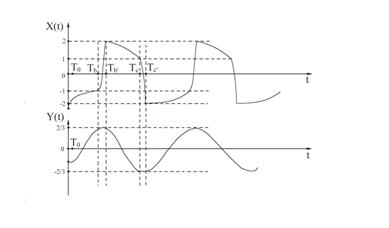
Рис. 1 .7. Компоненты решения уравнения
Ван дер Поля в зависимости от времени.

• Произвольная система нелинейных уравнений

В случае задачи Коши для общей системы нелинейных уравнений

, , ,

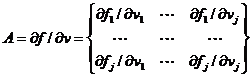, (18)

поведение ее решения вблизи некоторой точки определяется матрицей Якоби A .

Определение 1 . 1 . Система называется жесткой, если для всех t,v (т.е. на решениях (18)), собственные значения матрицы A удовлетворяют условиям:

, ,

, .

(т.е. расположены как на рис. 1 .4Г). Для оценки можно взять легко вычисляемую величину нормы матрицы A , для оценки – величину следа матрицы ; можно заменить на величину 1/Т, определяемую обычно из физики задачи. То есть простейшим критерием жесткости системы могут служить неравенства Т || A ||>>1, Sр( A )<<–1 (иногда ограничиваются даже одним условием (11)), однако надежных простых способов нет, и поэтому нужны численные методы, работающие без проверок на жесткость.

• Примеры простейших разностных схем для жестких ОДУ

• Способы построения схем

При численном решении задачи (18) с помощью разностных схем в некоторой последовательности точек вычисляются значения . Способов вычисления (разностных схем) изобретено множество, однако, не очень сильно отличаясь по качеству получаемого численного решения в стандартном случае (рис. 1 .4А), далеко не все из них пригодны для расчета жестких систем ОДУ (рис. 1 .4Г). В идейном плане можно выделить три основных подхода к их построению.

•  Одношаговые (двухточечные) методы типа Рунге–Кутты (схемы с пересчетом или схемы предиктор-корректор), пожалуй, наиболее популярны. Многие неявные варианты этих схем пригодны и для жестких систем. Здесь для вычисления v n требуется знание только v n+1 . Для неявных вариантов методов типа Рунге–Кутты косвенно используется матрица Якоби (несущая информацию о свойствах системы). В этих методах легко меняется шаг интегрирования в необходимых случаях. Могут быть построены методы достаточно высокого порядка точности. Вместе с тем требуется многократное вычисление правой части f в промежуточных точках , которые при переходе к новой точке не используются.

•  Многошаговые линейные методы (тоже могут быть и явными и неявными). При использовании этих методов не пропадает впустую информация в предыдущих точках , т.е. эти методы требуют меньшего числа вычислений f . Как и в одношаговых методах, в случае неявных схем косвенно используется информация о матрице Якоби A . Однако эти методы требуют “разгона” (вычисления дополнительных “начальных” значений в точках , получаемых другими методами). Для явных схем плохо с устойчивостью, возникают трудности с изменением шага интегрирования в процессе счета.

•  Не очень распространенный, но перспективный (в том числе для жестких систем) подход, связанный с переходом к продолженным системам :

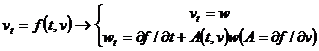(19)

Вводя расширенный искомый вектор u={v,w}, получаем для него уравнение

u t = B(t,v)u + r(t,v) , где

( r = 0, если f явно не зависит от t , т.е. в случае автономной системы). Увеличивая размерность u (т.е. вычисляя в точках t= t n не только v , v t = f , но и и т.д.), этот процесс можно продолжить (конечно, если f задается аналитически и соответствующие производные от f не очень громоздки).

•  Всевозможные гибриды из 1 , 2 , 3 и ряд других подходов.

• Требования к численным методам решения жёстких систем ОДУ

Каким же условиям должны удовлетворять разностные схемы для решения жестких систем? Разберем на примере системы (14) два простейших метода – явный и неявный методы ломаных, называемые также схемами Эйлера.

На участке пограничного слоя (его протяженность ) для воспроизведения решения пригоден практически любой обеспечивающий необходимую точность численный метод с шагом . Например, даже для явной схемы Эйлера в линейном случае (7)

имеем из условия устойчивости . Для примера (14),(16) (уравнение Ван дер Поля) , что не является здесь обременительным. Общее число шагов по времени ~10?100 тоже вполне приемлемо. Однако это ограничение на шаг интегрирования действует и на участках квазистационарного решения (С?B, B?C) и для прохождения таких участков потребуется уже шагов! А это уже неприемлемо при очень малых . Возможный выход – переход к решению предельной системы (15), в которой уже не фигурирует, а условие устойчивости (конечно, линеаризованное, т.е. действующее в небольшой окрестности кривой C?BB?CC?) или вполне приемлемо.

При численном решении на участках С?B и BС? полной системы (14), (16) хорошо работает неявный метод Эйлера

Для решения получающейся на каждом шаге по t нелинейной относительно v n+1 системы

используется какой-либо итерационный метод (например, метод Ньютона).

В случае линейной системы (7) в неявном методе Эйлера

(20)

условие устойчивости выполняется для любых при . Поэтому при использовании метода (20) для задачи (14),(16) на участках С?B, BС? нет проблем, исключая, конечно, тот факт, что матрица A плохо обусловлена для жестких систем и при обращении матрицы ( E – A ) могут возникнуть трудности при больших . Проведённый анализ показывает, (да и просто по графику x(t) на рис. 1 .7 видно), что шаг интегрирования на разных участках следует выбирать разным , и численный метод должен позволять это делать достаточно просто. Это первая характерная особенность жестких систем. То есть надо уметь предсказывать момент появления пограничных слоев, а это определяется собственными значениями матрицы Якоби. Отметим также, что в неявном методе Эйлера для системы (14)

,

,

т.е. приближенно мы как бы решаем предельную систему (15), так как .

Менять шаг интегрирования в процессе счета можно, но далеко не всегда нас интересует детальное поведение решения в пределах пограничного слоя. В таких случаях можно брать и по неявной схеме проходить пограничный слой за один шаг по времени.

Посмотрим еще, что будет происходить в неявной схеме вблизи точки B (или С) на примере уравнения Ван дер Поля (14), (16). Имеем:

,

.

Вблизи точки B с координатами {x n ,y n } имеем

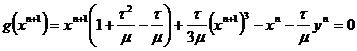, т.е. кубическое относительно искомого x n+1 уравнение, решения которого изображены на рис. 1 .8.

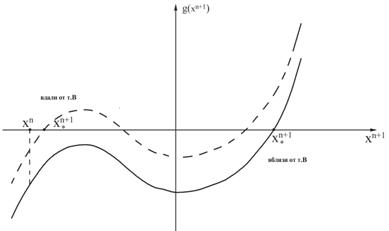
Рис. 1 .8. К алгоритму расчёта уравнения Ван дер Поля по неявной схеме Эйлера

Выбор в итерационном методе в качестве начального приближения {x n ,y n } при решении этого кубического уравнения может не дать сходимости. Это следствие вырождения исходной системы (14), и за этим надо следить (варьируя и т.п.). Например, задается некоторая точность сходимости итерационного процесса и минимально ( m ) и максимально ( M ) допустимые числа итераций. Если за M итераций процесс не сходится, уменьшают, если сходится за меньшее, чем m число итераций, то увеличивают и т.д.

Далее>>

вернуться к оглавлению