• Одношаговые методы типа Рунге–Кутты
• Алгоритм
Перейдем к общему случаю системы (18). Одношаговые методы типа Рунге–Кутты имеют вид
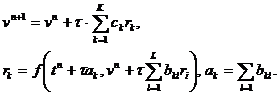 (21)
(21)
В дальнейшем для описания конкретных вариантов метода будем пользоваться таблицей Бутчера
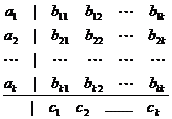
Для явных схем Рунге–Кутты L<k , и таблица Бутчера выглядит следующим образом:
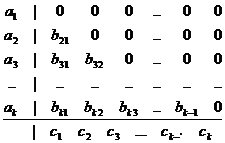
В этом случае для расчёта v n +1 по v n в соответствии с (21) имеем простые рекуррентные соотношения:
![]()
– предиктор,
![]() (22)
(22)
– первый корректор и т.д.
“Полуявные” или “диагонально неявные” схемы Рунге–Кутты отличаются от явных наличием ненулевых элементов на главной диагонали таблицы Бутчера ( L?k ):
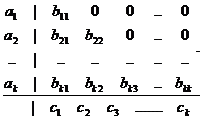
В этом случае на каждом шаге по времени последовательно решаются нелинейные системы
![]() ,
,
![]() и т.д., например, методом Ньютона
и т.д., например, методом Ньютона
![]()
![]()
с неким начальным значением ![]() , например,
, например, ![]() .
.
В общем случае ( L=K ), обозначая r = { r 1 ,…,r k } = {r 11 ,…,r 1j ,r 21 ,…,r 2j ,r k1 ,…,r kj } , имеем еще более громоздкую нелинейную систему
R(r) = 0 , где R = { R 1 , R 2 , ...,R k }
и итерационный процесс для ее решения
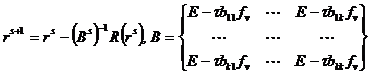
• Аппроксимация
Параметры схемы (неопределенные пока коэффициенты a 1 ,…,a k ,c 1 ,…,c k ,b 11 ,…,b 1k ,…,b k1 ,…,b kk ), конечно, не произвольны. Прежде всего, их (все или только часть) находят из условий аппроксимации, получаемых из разложения (21) в точке t=t n или t = t n +1 в ряд Тейлора с учетом (18) и его следствий
v t = f ( t , v ) , ![]()
(т.е. рассматривая аппроксимацию на решениях (18)).
Поскольку в (21) при к стоит множитель ![]() , то в разложении правой части (21) нужно удерживать на один член ряда Тейлора меньше, чем в левой. Индекс n будем опускать. Итак, левая часть (21):
, то в разложении правой части (21) нужно удерживать на один член ряда Тейлора меньше, чем в левой. Индекс n будем опускать. Итак, левая часть (21):
![]() Далее:
Далее:
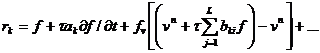 Если коэффициенты a k выбирать таким образом, чтобы
Если коэффициенты a k выбирать таким образом, чтобы
![]() , (23)
, (23)
то ![]() . Подставляя эти разложения в (21) и группируя члены при одинаковых степенях
. Подставляя эти разложения в (21) и группируя члены при одинаковых степенях ![]() , получим (после деления на
, получим (после деления на ![]() )
)
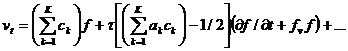
Очевидно, что при выполнении условия ![]() будем иметь первый порядок аппроксимации, при
будем иметь первый порядок аппроксимации, при ![]() – второй порядок аппроксимации и т.д. До четвертого порядка аппроксимации включительно эти условия имеют вид:
– второй порядок аппроксимации и т.д. До четвертого порядка аппроксимации включительно эти условия имеют вид:
![]() (24)
(24)
(вместе с (23) обеспечивает первый порядок аппроксимации),
![]() (25)
(25)
(вместе с (23),(24) обеспечивает 2-й порядок аппроксимации),
![]() (26)
(26)
(условия третьего порядка аппроксимации вместе с (23)-(25)),
![]()
![]() (27)
(27)
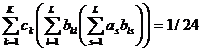 .
.
(условия четвертого порядка аппроксимации вместе с (23)-(26)). Уравнения (23)-(27) составляют относительно неопределенных коэффициентов некоторую нелинейную систему. Очевидно, что привлекаемое число условий аппроксимации (т.е. порядок точности схемы р при выполнении соответствующих условий гладкости) должно быть меньше числа отличных от нуля коэффициентов в (21), и соответствующая система должна быть разрешима. В частности, для явных схем ![]() , а для общих неявных схем
, а для общих неявных схем ![]() .
.
• Устойчивость
Конечно из того, что (21) при ![]() стремится к (18) еще не следует, что их решения будут сближаться. Как известно, для сходимости, по крайней мере, в линейном случае (
стремится к (18) еще не следует, что их решения будут сближаться. Как известно, для сходимости, по крайней мере, в линейном случае ( ![]() ), необходима еще устойчивость разностной схемы. А поскольку в линейном случае система (18) переходит в совокупность простейших уравнений типа (1) (только
), необходима еще устойчивость разностной схемы. А поскольку в линейном случае система (18) переходит в совокупность простейших уравнений типа (1) (только ![]() может быть и комплексным, т.е.
может быть и комплексным, т.е. ![]() ), при анализе устойчивости можно ограничиться изучением (1). Чтобы не погрязнуть в громоздких выкладках и иметь возможность графического представления некоторых результатов ограничимся также случаем K =2 в (21). Существа дела это не меняет, а для учебных целей вполне достаточно.
), при анализе устойчивости можно ограничиться изучением (1). Чтобы не погрязнуть в громоздких выкладках и иметь возможность графического представления некоторых результатов ограничимся также случаем K =2 в (21). Существа дела это не меняет, а для учебных целей вполне достаточно.
Итак, в случае модельного уравнения ![]() для обеспечения 2-го порядка аппроксимации из (23)-(25) имеем:
для обеспечения 2-го порядка аппроксимации из (23)-(25) имеем:
![]() (28)
(28)
Откуда
![]() , (29) т.е. четыре коэффициента
, (29) т.е. четыре коэффициента ![]() произвольны, а остальные четыре коэффициента определяются соотношениями (28),(29) (при условии не равенства нулю знаменателя в (29)).
произвольны, а остальные четыре коэффициента определяются соотношениями (28),(29) (при условии не равенства нулю знаменателя в (29)).
Из (26) с учетом (23),(29) имеем для схем 3-го порядка
3 ( b 11 + b 22 ) – 1 – 6 ( b 11 b 22 – b 12 b 21 ) = 0,
3[( b 11 + b 11 )+( b 21 + b 21 )]–6( b 22 + b 21 )( b 11 + b 12 )–2 = 0 . (30)
Для полуявных схем (b 12 =0) (30) определяет однопараметрическое семейство схем третьего порядка аппроксимации с коэффициентами
b 21 =1/[3(1– 2 b 11 )], b 22 =(1–3 b 11 )/[(1 –2 b 11 )], b 11 ![]() 1/2, (31)
1/2, (31)
а на четвертый порядок не хватает свободных коэффициентов.
Полагая далее ![]() ,
, ![]() , получим из (22):
, получим из (22):
v n +1 = q v n , (32)
![]()
![]() .
.
Действительно, для модельного уравнения в (21) r= l v ,
v 1 =v n + s (b 11 v 1 + b 12 v 2 +...+ b 1k v k ),
v 2 =v n + s (b 21 v 1 + b 22 v 2 +...+ b 2k v k ),
..........................................
v k =v n + s (b k1 v 1 + b k2 v 2 +...+ b kk v k ),
Или , обозначая v= { v 1 , ...,v k } , v n = { v 1 , ...,v n } , B= 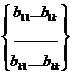 , имеем : ( E – s B ) v=v n , откуда v= ( E – s B ) v n =Dv n , D={d kj } ( т . е . v k = a k v n =
, имеем : ( E – s B ) v=v n , откуда v= ( E – s B ) v n =Dv n , D={d kj } ( т . е . v k = a k v n = ![]() ). Подставляя это выражение в (21), и получим (32).
). Подставляя это выражение в (21), и получим (32).
Геометрическая прогрессия (32) будет совпадать с точным решением v n +1 = v n e s , если q ( s ) =e s . Этот способ выбора коэффициентов в (21) называют методом экспоненциальной подгонки , его обобщение на случай линейной системы (7) ограничен лишь возможностями отыскания спектра матрицы A , а в случае нелинейной системы (18) может быть использована линеаризация (18) на малом отрезке [t n , t n +1 ].
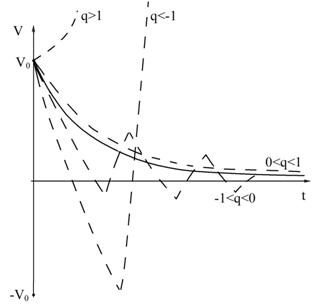
Так как мы рассматриваем здесь только случай Re( l )<0 (затухающие или устойчивые по Ляпунову решения), то при | q ( s )|>1 приближенное решение (32) не будет иметь ничего общего с точным решением. При разных действительных значениях s численное решение ведет себя как показано штриховыми линиями на рис. 1 .9 (точное решение – сплошная кривая).
То есть для устойчивости разностной схемы следует потребовать выполнения условия
| q ( s )| < 1 (33)
Для действительных l это эквивалентно условию –1< q ( s )<1.
Определение 1 . 2 . Схема называется абсолютно устойчивой, если (33) выполняется при всех значениях s.
Определение 1 . 3 . Схема называется монотонной, если 0<q( s )<1.
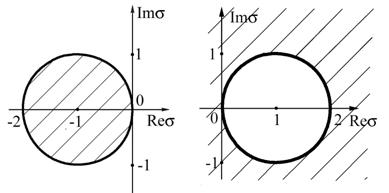
Если в комплексной плоскости (Re s , Im s ) нарисовать кривую | q ( s )| = 1, то она будет ограничивать область устойчивости . Примеры областей устойчивости для явного и неявного методов Эйлера показаны (заштрихованы) на рис. 1 .10А и рис. 1 .10Б, соответственно.
Рис. 1 .9 Вид численного решения при различных q |
|
|
А |
Б |
Рис. 1 .10. Области устойчивости схем Эйлера |
|
Для абсолютно устойчивых схем область устойчивости – вся комплексная плоскость s . Таких схем на практике не существует, но для жестких уравнений этого и не нужно, достаточно, чтобы схема была A -устойчивой (Дальквист, 1963 г .), как, например, неявная схема Эйлера, рис. 1.10Б.
Определение 1 . 4 . Схема называется A -устойчивой, если кривая |q( s )|=1 лежит в правой полуплоскости ? .
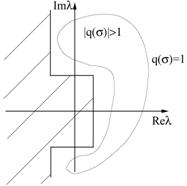
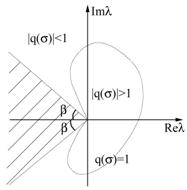
Это требование довольно тяжелое, поэтому его еще более ослабляют, требуя, чтобы кривая | q ( s )| = 1 лежала вне заштрихованных на рис. 1 .11А, Б областей (Гир, 1969г.). Это есть разные определения жестко устойчивых схем. Действительно, для жесткой системы ОДУ (рис. 1.4Г), если все Re( l j )<0, то при изменении t от 0 до ? все точки s j = tl j на плоскости { Re s , Im s } будут двигаться по радиальным направлениям внутри некоторого угла 2 ? (рис. 1 .11Б), оставаясь внутри области устойчивости.
|
|
А |
Б |
Рис. 1 .11. Области устойчивости жёстко устойчивых схем |
|
Величина Re q ( s ) определяет скорость затухания решения. При Re l << –1 точное решение затухает очень быстро, значит и численный метод при | s | ® ? (точнее при Re s ® – ? ) должен обладать этим свойством.
Определение 1 . 5 . Схема называется L -устойчивой (Ламберт, 1973 г .) , если
| q( s ) | ® 0 при | s | ® ? (или Re q( s ) ® 0 при Re s ® – ? ) (34)
Обобщение всех этих определений на случай линейной системы (7) очевидно, надо, чтобы соответствующие условия выполнялись для всех s j = t l j ( l – собственные значения матрицы A ). Для общей нелинейной системы (18) все это должно выполнятся локально, при всех t n (принцип линеаризации и замораживания коэффициентов).
• Примеры схем Рунге–Кутты
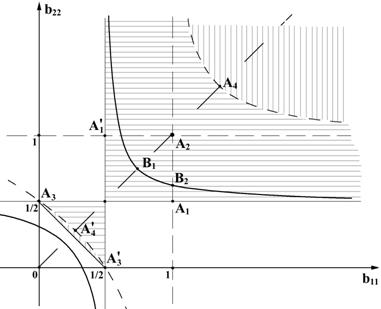
Рис. 1 .12. Полуявные схемы Рунге–Кутты в плоскости неопределённых коэффициентов ( K =2) |
Вернемся теперь к конкретному выражению для q из (32) и для простоты ограничимся случаем действительных l <0. Это особенно не меняет существа дела, но упрощает выкладки. Будем также полагать b 12 = 0 (полуявные схемы), тогда q не зависит также и от b 21 , а оставшиеся два свободных коэффициента примем за оси координатной плоскости, в которой будем вести рассмотрение (рис. 1 .12).
Область устойчивых при всех – ? < s < 0 схем, т.е. область A- устойчивых схем –1 < q ( s ) < 1 на рис. 1 .12 заштрихована (горизонтальная штриховка: –1 < q (– ? ) < 0, вертикальная штриховка 0 < q (– ? ) < 1).
Множество схем третьего порядка аппроксимации (31) на рис. 1 .12 показано сплошной кривой (гипербола с асимптотами b 11 = 1/2, b 22 = 1/2).
Для L -устойчивых схем из (32), (34) имеем
b 11 b 12 – ( b 11 + b 12 )+1 / 2 = 0, ( b 11 + b 12 )?1 / 2 (35)
На рис.1.12 L -устойчивым схемам (35) соответствует штриховая кривая (гипербола с асимптотами b 11 = 1, b 22 = 1). Видно, что в данном случае (среди полуявных схем Рунге–Кутты с K =2) ни L-устойчивых, ни монотонных схем третьего порядка нет , а L -устойчивые схемы второго порядка расположены на кривых A 3 A 4 ? A 5 ? и A 4 .
Несколько конкретных примеров. На прямой b 11 =b 22 , проходящей через точки O, A 4 ? , B 1 , A 2 , A 4 , расположены схемы Бутчера. Точка A 3 (и точка A 3 ? , так как точкам, симметричным относительно прямой b 11 =b 22 соответствует формальная замена в (21), (22) индекса 1 на 2 и наоборот) соответствует схеме Лобатто, для которой таблица Бутчера имеет вид:
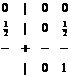 или
или 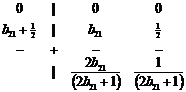 ( b 21 ?–1/2) (36)
( b 21 ?–1/2) (36)
Это полуявная (с явным предиктором, т.е. достаточно экономная по объему вычислений) схема второго порядка аппроксимации. Она расположена на границе области A- устойчивых схем, не L -устойчива ( q (– ? ) = –1) и монотонна лишь при –2 < s < 0.
Точка A 1 (и симметричная ей точка A 1 ? ) также расположена на границе области A- устойчивых схем, не L- устойчива ( s (– ? ) = –1), монотонна лишь при –1– ![]() < s < 0 и по своим свойствам мало отличается от схемы Лобатто. Соответствующая ей таблица Бутчера имеет вид:
< s < 0 и по своим свойствам мало отличается от схемы Лобатто. Соответствующая ей таблица Бутчера имеет вид:
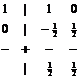 или
или 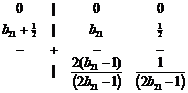 ( b 21 ?1/2) (37)
( b 21 ?1/2) (37)
Точка A 2 является A- устойчивой, но не L - устойчивой схемой ( s (– ? ) = –1/2), монотонна при –1– ![]() < s < 0, как и схема A 1 , имеет второй порядок аппроксимации, по своим свойствам несколько лучше предыдущих схем. Соответствующая ей таблица Бутчера имеет вид:
< s < 0, как и схема A 1 , имеет второй порядок аппроксимации, по своим свойствам несколько лучше предыдущих схем. Соответствующая ей таблица Бутчера имеет вид:
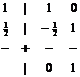 или
или 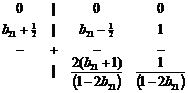 ( b 21 ? 1/2) (38)
( b 21 ? 1/2) (38)
Точки A 4 и A 4 ? являются примерами A- и L - устойчивых схем (точка A 4 также монотонна при всех отрицательных значениях s ) второго порядка аппроксимации. В соответствующей им таблице Бутчера знак ‘+' относится к схеме A 4 , а знак ‘–' – к A 4 ? :
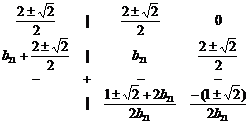 , b 21 ? 0 (39)
, b 21 ? 0 (39)
Схема Хаммера–Холлингсвудта – второго порядка аппроксимации, полностью неявная, не L - устойчивая ( q (– ? ) = 1, пример неудачной схемы):
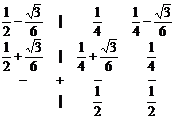
Явная схема Эйлера – Коши (точка 0):
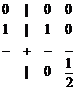 (40)
(40)
Две полуявные (с неявными предикторами и корректорами) схемы третьего порядка, не L - устойчивые, немонотонные, A- устойчивые:
1) точка B 1 (схема Розенброка)
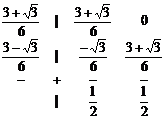 (41)
(41)
2) точка B 2 , для которой
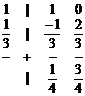 (42)
(42)
Основная гипотеза, принимаемая здесь и в дальнейшем при анализе разностных схем: точкам в пространстве неопределенных коэффициентов {b k 1 }, которые близки между собой (в смысле расстояния, например, в евклидовой метрике), соответствуют схемы, близкие по своим свойствам (точности, устойчивости и т.п.).