• Линейные многошаговые схемы (методы типа Адамса).
• Алгоритм и аппроксимация
Используя, как и в разделе 1.3 , метод неопределенных коэффициентов и записывая линейную комбинацию вектор-функций v и правых частей f в некоторой последовательности равноотстоящих точек t n , t n +1 , ..., t n + k ( t = t n + k t – t n + k = const ), для линейных многошаговых методов получим следующее разностное выражение:
(43)
Из-за однородности (43), коэффициент при искомом значении v n + k можно выбрать единичным:
а K = 1 (44)
Неопределенные коэффициенты a k , b k ( k =0 ,...,K ) из разложения (43) в ряд Тейлора в точке t n + k (или t n ) связаны условиями аппроксимации (на решениях (18) ):
, 
(45)
(обеспечивают первый порядок аппроксимации),
(46)
(обеспечивает второй порядок аппроксимации вместе с (45)),
…
(47)
(обеспечивает n –ый порядок аппроксимации на решениях (18) вместе с предшествующими условиями).
Схемы первого порядка аппроксимации малоинтересны, поэтому в дальнейшем будем рассматривать схемы второго или более высокого порядка точности. Если с учетом нормировки (44) и условий аппроксимации второго порядка точности (45), (46) исключить, например,
,
,
.
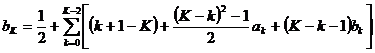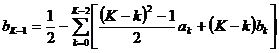то оставшиеся свободными коэффициенты (если позволяет выбранное K> 2), можно принять за линейное пространство размерности 2( K –1), например, с евклидовой метрикой, и каждой точке в этом пространстве будет соответствовать некоторая разностная схема второго порядка точности, а условия более высокого порядка аппроксимации ((47) при n =3 и т.д.) после исключения в них a k , a k –1 , b k , b k –1 , являясь относительно оставшихся свободными коэффициентов a k , b k ( k= 0,…, K –2) линейными уравнениями
,
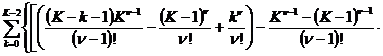
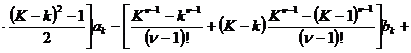
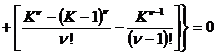образуют в этом пространстве соответствующую гиперплоскость схем третьего порядка аппроксимации. На пересечении двух таких гиперплоскостей ((47) при n =3 и n =4) будут расположены схемы с четвертым порядком аппроксимации и т.д., пока мы не исчерпаем все возможности для выбранного K , т.е. пока не найдем единственную схему с наиболее высоким (для данного K ) порядком аппроксимации (одну из точек в этом пространстве).
В частности, при K = 2 имеем:
a 2 = 1 , a 1 = –1– a 0 ,
b 2 = (1+ a 0 +2 b 0 ) / 2 , b 1 = (1–3 a 0 –4 b 0 ) / 2, (48)
где a 0 и b 0 произвольны для схем второго порядка аппроксимации.
Условие третьего порядка аппроксимации дает прямую в плоскости {a 0 , b 0 } с уравнением
5 a 0 + 12 b 0 + 1 = 0,
а единственной схемой четвертого порядка аппроксимации будет точка на этой прямой с координатами:
a 0 = –1 , b 0 = 1/3 . (49)
• Устойчивость
Как уже отмечалось, одной аппроксимации недостаточно для сходимости решений (43) к решениям исходной дифференциальной задачи даже в линейном случае (7). Необходимо еще обеспечить устойчивость разностных схем (43). Для одного линейного уравнения, полагая f= l v из (43) получим
. (50)
Устойчивость разностных схем (50) будем исследовать на специальных решениях вида v n =q n . Тогда для определения q имеем многочлен устойчивости степени K и уравнение
,
корни которого q j , j =1 , 2 ,...,K (действительные или комплексные, в зависимости от s , a k , b k ) должны удовлетворять условиям устойчивости
| q ( s ) | < 1, j =1 ,...,K. (51)
Если в плоскости { Re s , Im s } область устойчивости, определяемая неравенствами (51), включает всю левую полуплоскость (т.е. (51) выполняется для всех s с Re s < 0), имеем A- устойчивую схему. Если эта область включает в себя заштрихованную на рис. 1 .11А или 1 .11Б часть плоскости { Re s , Im s } , имеем жестко устойчивую схему. Если
| q ( s ) | = 0, j= 1 , 2 ,...,K , (52)
то схема будет L -устойчивой.
Для действительных s и q j ( s ) условия устойчивости схемы будут иметь вид
–1 < q j ( s ) < 1 .
Если это условие выполняется для всех s : – ? < s < 0, то схема A- устойчива, если выполняется (52), то она L- устойчива.
• Примеры линейных многошаговых схем
Для случая K= 2 с учетом (48),(50) имеем
v n +2 = a 1 v n +1 + a 0 v n , q 2 – a 1 q – a 0 = 0 .
Отсюда
, 
,
где
,
.
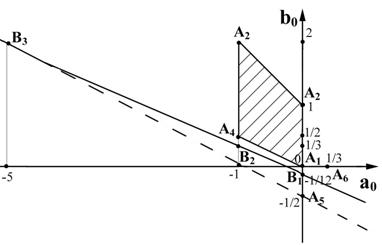
Рис. 1 .13. Линейные многошаговые схемы в плоскости неопределённых коэффициентов ( K =2) |
Условия | q 1 ( s , a 0 , b 0 )|?1, | q 2 ( s , a 0 , b 0 )|?1 ограничивают область A- устойчивых схем. На рис. 1 .13 эта область в плоскости свободных коэффициентов {a 0 , b 0 } заштрихована (четырехугольник A 1 , A 2 , A 3 , A 4 ). Сплошная прямая B 1 B 2 – множество схем с третьим порядком аппроксимации. Как видно, среди них нет A - устойчивых. Точка B 2 на этой прямой – единственная в этом случае схема четвертого порядка аппроксимации (49). И в самом общем случае доказано (теорема Дальквиста), что линейных многошаговых A-устойчивых схем с порядком аппроксимации выше второго не существует.
Точка A 6 с координатами a 0 = 1 / 3, b 0 = 0 (53)
– единственная в этом случае L- устойчивая схема (схема Куртиса–Хиршфельдера). Область жестко устойчивых схем, очевидно, содержит внутри себя множество A- устойчивых схем. В частности, схема, соответствующая точке A , является жестко устойчивой.
Точка A 1 с коэффициентами
a 0 =b 0 = 0, (54)
т.е. одношаговая линейная схема (метод трапеций), из числа A- устойчивых схем является оптимальной в том смысле, что она среди других A- устойчивых схем при K = 2 ближе всего расположена и к L- устойчивой схеме (точке A 6 ), и к схемам 3–го порядка точности (наиболее точная из A- устойчивых схем).
Отметим еще схему третьего порядка точности, соответствующую точке B 1 . Она является жестко устойчивой и наиболее близка к множеству A- устойчивых схем. Для этой схемы
a 0 =0, b 0 =– 1/12. (55)
Явным схемам на рис. 1 .13 соответствует штриховая прямая. В частности, точка A 5 с коэффициентами
a 0 = 0, и = –1/2 (56)
– явная схема Адамса. Все явные схемы, как видно, не являются A- устойчивыми. А в целом, семейство линейных многошаговых схем существенно беднее схем типа Рунге – Кутты.
• Схемы для продолженных систем (схемы Обрешкова).
• Алгоритм и аппроксимация
Лучшие черты методов Рунге–Кутты и линейных многошаговых методов сочетают схемы для продолженной системы (19) или линейные многошаговые схемы, использованием 2-й (схемы Обрешкова) и более высоких производных
v tt ( t,v ) = f t = ¶ f/ ¶ t + f v f, (57)
Добавляя в (43) линейную комбинацию вторых производных v tt с дополнительными неопределенными коэффициентами с k , получим для этих схем ( a K =1)
или, что то же
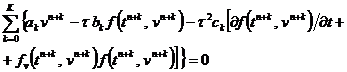(58)
Из начальных условий в (18) и из (57) видно, что v tt (0, v 0 ) фактически можно считать известным.
Условия аппроксимации, как и в случае линейных многошаговых методов, являются линейными ( относительно неопределенных коэффициентов a k , b k , c k ) уравнениями
, 
, (59)
(обеспечивают первый порядок аппроксимации),
(60)
(обеспечивает второй порядок аппроксимации вместе с (59))
...
(61)
(обеспечивает n –ый порядок аппроксимации на решениях (18) вместе с предшествующими условиями).
В случае неявных схем ( b K ? 0, c K ? 0) для решения нелинейной относительно v n + k системы (58) с ограничениями (59)-(61)
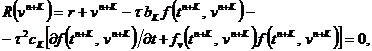
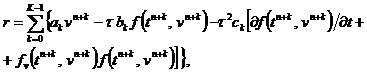
следует воспользоваться каким–либо итерационным методом, например,
– B –1 ( t n + k , 
) R ( 
), s =0 , 1 ,...,
= v n + k –1 ,
B = ¶ R / ¶ v n + k = E – t b k f v – t 2 c k [ ¶ ( ¶ f / ¶ t ) / ¶ v + f v f v + C ]. (62)
В (62) С – матрица, столбцами которой являются векторы
( ¶ ( f v ) / ¶ v 1 ) f, ( ¶ ( f v ) / ¶ v 2 ) f, ..., ( ¶ ( f v ) / ¶ v k ) f. (63)
• Устойчивость
Так как свободных параметров у этого класса разностных схем больше, появляется возможность при меньшем числе точек сеточного шаблона (т.е. при меньших K ) строить схемы более высокого порядка аппроксимации, чем в случае линейных многошаговых схем. В частности, при K =1 (одношаговые, как методы Рунге–Кутты, схемы) имеем для схем второго порядка аппроксимации
a 1 = 1 , a 0 = –1 , b 0 = 1 / 2+ c 0 + c 0 , b 1 = 1 / 2– c 0 – c 1 , (64)
c 0 ,c 1 – произвольны. Если в дополнение к (64)
c 1 =c 0 –1 / 6, (65)
то имеем однопараметрическое семейство схем третьего порядка аппроксимации, а при
c 0 = 1 / 12 , c 1 = – 1 / 12 (66)
– единственную на данном сеточном шаблоне схему четвертого порядка аппроксимации.
Для тестового уравнения с f = l v имеем
v t =f = l v, v tt =f t = l v= l 2 v, ...,
т.е. то же, что и в случае линейных многошаговых схем. В частности, при K =1, как и в методах Рунге–Кутты, получаем геометрическую прогрессию
v n+1 = q v n , где q = – a 0 /a 1 =
= [ 1+ s (1 / 2+ c 0 + c 1 )+ s 2 c 0 ] / [ 1– s (1 / 2– c 0 – c 1 )– s 2 c 1 ]. (67)
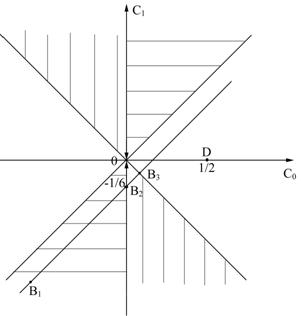
Рис. 1 . 14. Схемы Обрешкова в плоскости неопределённых коэффициентов ( K =1) |
Из условия устойчивости | q ( s ? , c 0 , c 1 )| < 1, требуя его выполнения для всех значений s : – ? ?Re( s )?0, в плоскости свободных параметров {c 0 , c 1 } можно получить все множество A- устойчивых схем (заштриховано на рис. 1 .14, вертикальная штриховка – монотонные схемы, для которых, в случае действительных значений s 0 < q ? 1 , горизонтальная штриховка – устойчивые, но не монотонные схемы, для которых 1? q <0).
Определяя из (67) 
| q ( s , c 0 , c 1 )| = – c 0 /c 1 , и приравнивая его нулю, получим, что множество L- устойчивых схем расположено на прямой с 0 = 0 (исключая точку с 1 = 0).
Схемам третьего порядка аппроксимации (65) на рис. 1 .14 соответствует прямая B 1 B 2 B 3 , единственной схеме четвертого порядка (66) – точка B 3 , расположенная на границе A- устойчивых схем.
Точка O с координатами
с 0 =0, с 1 =0 (68)
соответствует известной схеме “трапеций”.
В целом данный класс разностных схем заметно богаче линейных многошаговых схем, в частности, он содержит целую полупрямую B 1 B 2 A- устойчивых схем третьего порядка аппроксимации, в том числе L -устойчивую схему – точку B 2 с координатами
c 0 = 0, c 1 = –1 / 6, (69)
чего нет даже в методах Рунге–Кутты при K =2. Заканчивая данный раздел, отметим, что в нем затронуты лишь самые основные понятия и методы, используемые при численном решении жестких систем ОДУ. С более детальным их изложением читатель может ознакомиться в многочисленной оригинальной литературе (обзор которой можно найти, например, в [5]) и в книгах [6–9]. Основные усилия исследователей в данной области направлены на построение эффективных безытерационных методов, исследованию сходимости численных методов для нелинейных уравнений и смежным вопросам.
• Примеры жёстких систем ОДУ
• Модель Филда–Нойса «орегонатор»
Простейшая математическая модель периодической химической реакции Белоусова–Жаботинского состоит из трех уравнений:
На то, что система жесткая, указывают большие различия в константах скоростей реакций — есть процессы «быстрые» и есть «медленные».
Так как переменные системы — концентрации ( HbrO 2 , Br – и Ce ( IV ) соответственно) то начальные условия для системы следует выбирать положительными. Как правило, их выбирают достаточно близкими к 0. Конечное время интегрирования системы T k = 800.
О системе см., например, [1–3] .
• Уравнение Ван-дер-Поля
Типичным примером жесткой задачи малой размерности является уравнение Ван-дер-Поля [1, 2, 4, 5]. Его возможно записать в виде системы
(1)
или в виде:
, (2)
(представление Льенара). Считаем, что параметр a — большой. В расчетах рассмотреть два случая: a = 10 3 и a = 10 6 . Для тестов обычно полагают 
Конечное время интегрирования системы, записанной в виде (1), T k = 20.
Периодические решения жестких систем ОДУ иногда называют релаксационными автоколебаниями [4, 5].
Дополнительный вопрос: укажите преобразование, переводящее представление (1) в представление Льенара (2).
• Система Ван-дер-Поля и траектории-утки
Рассмотрим неавтономную систему уравнений Ван-дер-Поля:
Как и в предыдущей задаче считаем, что a = 10 3 и a = 10 6 , 
Рассмотреть численно случаи 0 < A < 1 и 
T k = 200.
О траекториях-утках в системе Ван-дер-Поля см. [5] (строгое математическое исследование) и [6] (популярное изложение).
• Суточные колебания концентрации озона в атмосфере
Рассмотрим простейшую математическую модель колебаний концентрации озона в атмосфере [7]. Она описывается следующей неавтономной системой ОДУ:
В данной модели уравнения описывают изменение концентрации атомарного кислорода, молекулярного кислорода и озона соответственно. Считается, что изменения концентрации молекулярного кислорода невелики. Начальные значения для задачи таковы:
(см –3 ), 
(см –3 ), 
(см –3 ),
значения констант скоростей химических реакций:
, 
.
Две другие химические реакции зависят от локальной освещенности участка земной поверхности и приближаются следующим выражением:
где 
с –1 , с 3 = 22,62, с 4 = 7,601. Значения констант скоростей обращаются в ноль «ночью», резко возрастают «на рассвете», достигают максимума «в полдень» и падают до ноля «на закате». Конечное время интегрирования T k = 172 800 c (двое суток).
Данная система является жесткой «ночью» и умеренно жесткой «в светлое время суток».
• Уравнение Бонгоффера — Ван-дер-Поля
Рассмотрим еще один пример жесткой задачи малой размерности, имеющей периодическое решение [5, 8].
Здесь a = 10 3 и a = 10 6 , 
Уравнение описывает протекание тока через клеточную мембрану. Постоянная компонента тока c в безразмерной записи системы такова, что 0 < c <1, b > 0. T k = 20.
• Сингулярно - возмущенная система — модель двухлампового генератора Фрюгауфа
Система более высокой размерности, имеющая решение в виде релаксационного цикла, приведена в [4] (см. также [8]). Она имеет вид:
Здесь ? > 0 — константа порядка единицы, функция
T k = 20, ? = 10 –3 , 10 –6 .
• Простейшая модель гликолиза
Простейшая модель гликолиза описывается уравнениями следующего вида [8]:
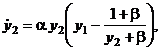
предложенными Дж. Хиггинсом. В системе ? = 10, ? = 100, 200, 400, 1000. Начальные условия для системы: y 1 (0) = 1, y 2 (0) = 0,001, T k = 50. Решение этой системы — релаксационные автоколебания (жесткий предельный цикл).
• Модель химических реакций Робертсона
Один из первых и самых популярных примеров «жесткой» системы ОДУ принадлежит Робертсону (1966) и имеет вид, типичный для моделей химической кинетики — в правой части системы стоят полиномы второй степени от концентраций (сравните с орегонатором).
Система Робертсона имеет вид [1]:
Начальные условия для системы таковы: y 1 (0) = 1, y 2 (0) = 0, y 3 (0) = 0. Рассматриваются следующие величины отрезка интегрирования: T k = 40 (в работе Робертсона рассматривался именно такой отрезок интегрирования), T k = 100, 1000, …, 10 11 . О свойствах задачи см. в [1].
• Модель дифференциации растительной ткани
Данный пример из [1] — типичный случай биохимической модели «умеренной» размерности (современные модели, например, фотосинтеза включают сотни уравнений подобного типа). Хотя данная модель является умеренно жесткой, тем не менее, ее лучше решать с помощью методов, предназначенных для решения ЖС ОДУ.
Начальные значения всех переменных системы равны 0, кроме y 1 (0) = 1 и y 8 (0) = 0.0057. Длина отрезка интегрирования T k = 421,8122.
• Задача E5
Еще одна модель химической реакции из [1], получившая свое название Е5 в более ранних публикациях.
Начальные условия: y 1 (0) = 1,76•10 –3 , а все остальные переменные равны 0. Значения коэффициентов модели следующие: A = 7,89•10 –10 , B = 1,1•10 7 , C = 1,13•10 3 , M = 10 6 . Первоначально задача ставилась на отрезке T k = 1000, но впоследствии было обнаружено, что она обладает нетривиальными свойствами вплоть до времени T k = 10 13 (подробнее см. [1]).
Обратите особое внимание, что в процессе расчетов приходится иметь дело с очень малыми концентрациями реагентов (малы значения y 2 , y 3 и y 4 ). Как «подправить» постановку задачи E5?
• Уравнение Релея
Уравнение Релея во многом похоже на уравнение Ван-дер-Поля [8]. Рассматривается задача вида
.
Решить задачу, записав уравнение Релея в виде системы ОДУ. Начальные условия: x (0) = 0, 
? = 1000, T k = 1000.
• Экогенетическая модель
Рассмотрим пример системы уравнений, которая описывает изменения численности популяций двух видов и эволюцию некого генетического признака ? . Система ОДУ имеет вид:
Параметры задачи таковы: ? ? 0,01, 0 ? x 0 ? 3, 0 ? y 0 ? 15, ? 0 = 0, T k = 1500. Наличие малого параметра в третьем уравнении системы показывает, что генетический признак меняется медленнее, чем численность популяций. Решение системы — релаксационные колебания.
Задача описана в статье [9].
• Экогенетическая модель
Еще один пример жесткой системы описан в статье [9]. Более интересный случай — численность двух популяций зависит от взаимодействия между ними и двух медленно меняющихся генетических признаков.
Параметры задачи таковы: ? ? 0,01, 0 ? x 0 ? 40, 0 ? y 0 ? 40, ? 10 = 0, ? 20 = 10, T k = 2000.
Рассмотреть также модификацию предыдущей системы [9]:
Параметры задачи: ? ? 0,01, 0 ? x 0 ? 40, 0 ? y 0 ? 40, ? 10 = 0, ? 20 = 10, T k = 2000.
Литература
• Э. Хайрер, Г. Ваннер . Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально – алгебраические задачи. — М.: Мир, 1999. — 685 с.
• Э. Хайрер, С. Нерсетт, Г. Ваннер . Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. — М.: Мир, 1990. — 512 с.
• Колебания и бегущие волны в химических системах: Пер. с англ. / Под ред. Р. Филда, М. Бургер . — М. : Мир, 1988. — 720 с.
• Е. Ф. Мищенко, Н. Х. Розов . Дифференциальные уравнения с малым параметром и релаксационные колебания. — М.: Наука, 1975. — 248 с.
• Е. Ф. Мищенко, Ю. С. Колесов, А. Ю. Колесов, Н. Х. Розов . Периодические движения и бифуркационные процессы в сингулярно-возмущенных системах — М.: Наука. Физматлит, 1995. — 336 с.
• Г. Г. Малинецкий Хаос. Структуры. Вычислительный эксперимент. — М.: Наука, 1998. (или Эдиториал УРСС, 2000.)
• Д. Каханер, К. Моулер, С. Нэш. Численные методы и программное обеспечение. — М.: Мир, 1998. — 575 с.
• П. С. Ланда . Нелинейные колебания и волны. — М.: Наука. Физматлит, 1997. — 496 с.
• А. С Кондрашов, А. И. Хибник. Экогенетические модели как быстро-медленные системы. / В кн.: Исследования по математической биологии. – Пущино, 1996. — с. 88–123.
• Ракитский Ю.В.,Устинов С.М., Черноруцкий И.Г. Численные методы решения жестких систем. – М.: Наука, 1979 (п.п. 1-4).
• Холл Дж., Уатт Дж. (ред.). Современные численные методы решения обыкновенных дифференциальных уравнений. – М.: Мир, 1979 (п.п.1-4).
• Калиткин Н.Н. Численные методы. – М.: Наука, 19?? (п.12).