Магистерская работа:
"Методы преобразования сигналов входными цепями системы виброакустической диагностики"
План
- Проблемы вибродиагностики
- Математические модели вибросигналов
- Структура аппаратных средств системы виброакустической диагностики
Литература
Проблемы вибродиагностики
Виброакустическая диагностика, являясь разделом технической диагностики, есть отрасль знаний, включающая в себя теорию и методы организации процессов распознавания технических состояний машин и механизмов по исходной информации, содержащейся в виброакустическом сигнале.
Вибродиагностика - это одна из относительно новых отраслей науки, основанная на предположении, что любой объект (технический, биологический и т. д.) может быть представлен в виде колебательной системы и спектра вибросигнала, стимулированного либо тестом, либо функциональными возмущениями, содержащих информацию о техническом состоянии, дефектах и качестве объекта. Способ извлечения и расшифровки этой информации составляют основную задачу диагностики, которая в последнее врямя решается в с помощью вычислительной техники. Различают функциональную и тестовую диагностику. Под функциональной диагностикой чаще всего подразумевают виброакустическую диагностику, а под тестовой - определение технического состояния с помощью искусственно создаваемой вибрации.
Методы вибродиагностики направлены на обнаружение и идентификацию таких неисправностей агрегата, которые оказывают влияние на его вибрацию: дефектов роторов, опорной системы и узлов статора и т.д., испытывающих либо генерирующих динамические нагрузки. Сначала использовались методы и средства контроля различных параметров, затем мониторинга, и, на последнем этапе, системы диагностики и прогноза технического состояния. Внедрение каждого последующего вида систем дает пользователю новые возможности для перехода на обслуживание машин и оборудования по фактическому состоянию. [ 1 ] Основными целями вибродиагностики являются:
- сокращение расходов на обслуживание;
- предупреждение развития дефектов агрегата и сокращение затрат на его восстановление;
- улучшение качества обслуживания;
- увеличение срока службы механизма.
Задачами вибродиагностики являются:
- разделение множества возможных технических состояний агрегата на два подмножества: исправных и не исправных;
- постановка диагноза, состоящего в определении характера и локализации одного или группы дефектов, соответствующих вибрационному состоянию агрегата;
- возможное обнаружение дефекта на ранней стадии и прогнозирование его развития во времени.
На основании диагноза определяется оптимальный режим эксплуатации агрегата в условиях возникшей неисправности и технология устранения дефекта и восстановления работоспособности агрегата. Чем надежней и конкретней диагноз, тем ниже затраты, связанные с восстановлением агрегата.
В моей магистерской работе я занимаюсь методами преобразования исходных вибросигналов в элементах измерительного канала, и результатом работы является формулировка рекомедаций по определению оптимальных параметров устройств для различных видов вибросигналов.
Математические модели вибросигналов
Машина, элементы которой совершают вращательное движение, генерирует механические колебания сложной формы. Причинами этих колебаний являются физические взаимодействия элементов, связанные с разбалансом, люфтом, изгибом валом, несоосностью, дефектами элементов машины и др. Эти сложные колебания несут большой объем информации о динамических явлениях происходящих в работающей машине и могут быть зарегистрированы на корпусных деталях машины как вибрации. Среди всего объема содержащейся в этих колебаниях информации необходимо выделить ту, которая позволяет идентифицировать дефекты элементов машин и развитие этих дефектов.
При проведении последующего анализа полученного вибросигнала, сигнал представляется в частотной и временной областях. Временной анализ сигнала позволяет судить об изменении сигнала во времени, анализировать изменение амплитуды, а также увеличение влияния высших гармоник сигнала. Анализ в частотной области позволяет позволяет проводить спектральный анализ, дающий возможность выявить влияние отдельных частотных составляющих на результирующий сигнал.
Например, на представленном ниже анимированном рисунке видно, как развивается дефект подшипника, при его мониторинге в частотной области (путем анализа спектра):
Анимация.1 - Спектры вибрации при развитии дефекта подшипника качения
На первой стадии развития дефекта в спектре, наряду с первыми, механическими, гармониками оборотной частоты вращения ротора, появляется пик на характерной частоте дефекта того или иного элемента подшипника. На этой стадии характерная гармоника уже хорошо видна на спектре и позволяет достаточно точно выявлять дефектный элемент.
Дальнейшее развитие дефекта приводит к появлению гармоник от характерной подшипниковой частоты. Обычно появляются гармоники с номером два и три от основной частоты подшипникового дефекта. Рядом с каждой такой гармоникой слева и справа тоже будут иметь место боковые частоты, число пар которых может быть достаточно большим. Чем более развит дефект, тем больше боковых гармоник и у гармоник частоты дефекта.
Износ подшипника с таким спектром уже очевиден и может простираться почти по всей рабочей поверхности подшипника, он уже стал групповым, захватив несколько элементов подшипника. Подшипник нуждается в замене или к такой процедуре нужно интенсивно готовиться.
Это последняя стадия развития дефектов подшипника. Затраты на трение велики и вращение ротора затруднено. Износ подшипника достигает такой стадии, когда характерная частота дефекта из - за износа становится нестабильной, такая же участь постигает боковые гармоники. Наложение многих семейств гармоник, каждое из которых состоит из основной частоты и боковых гармоник, создает достаточно сложную картину. Если в этих семействах основные гармоники различаются по частоте немного, то сумма всех частот представляет из себя общее поднятие спектра, "энергетический горб", захватывающий такой диапазон частот, куда входят все гармоники всех семейств от всех уже существующих дефектов подшипника качения.
Для представления сигналов в частотной и временной областях используется преобразование Фурье, являющееся математической основой, которая связывает временной или пространственный сигнал (или же некоторую модель этого сигнала) с его представлением в частотной области. [ 2 ] Преобразование Фурье для непрерывного сигнала h(t) является преобразованием Лапласа относительно некоторой функции f, определяемой выражением:
В этой формуле H(f) называется преобразованием Фурье с непрерывным временем (или непрерывно временным преобразованием Фурье, НВПФ). Переменная f в комплексной синусоиде exp(-j2pf) соответствует частоте, измеряемой в герцах, если переменная t измеряется в единицах времени (в секундах). По сути дела, НВПФ идентифицирует частоты и амплитуды тех комплексных синусоид, на которые разлагается некоторое произвольное колебание. Обратное преобразование Фурье определяется выражением:
Значения информативных параметров вибросигнала можно оценить на основе представления сложных колебаний в виде суммы более простых составляющих. Вибросигнал можно представить в виде 3-х составляющих: флуктуационной составляющей, импульсной составляющей, а также случайной составляющей в виде шумов.
Флуктуационная составляющая характеризуется непрерывностью и относительной плавностью своего изменения. Причиной ее возникновения являются динамические процессы, время развития которых соизмеримо со временем цикла механизма и которые протекают на низких частотах, близких к собственным частотам его вращения. Эти явления обусловлены небалансом, несоосностью, ослаблением механических связей конструкции, изгибом вала, волнистостью тел качения, неравномерным абразивным износом. Несмотря на то, что каждая из этих причин порождает, как правило, периодическую компоненту в сумме они формируют сложное квазислучайное колебание.
Флуктуационную составляющую можно представить в следующем виде:
где Аij - амплитуда виброускорения j-й гармоники i-й компоненты флуктуационной составляющей;
 - функция, описывающая изменение флуктуационной составляющей виброускорения во времени, представленное в виде ряда Фурье; - функция, описывающая изменение флуктуационной составляющей виброускорения во времени, представленное в виде ряда Фурье;
 ij - частоты соотвествующих гармоник; ij - частоты соотвествующих гармоник;
 ij - фазовый сдвиг соотвествующих гармоник. ij - фазовый сдвиг соотвествующих гармоник.
В частотной области, путем использования НВПФ, получим:
Шумовая составляющая сигнала проявляется вследствие случайных факторов при работе машины или механизма. Это может быть, например, попадание мелких частиц в смазку подшипника или оказание внешних воздействий (изменение нагрузки) на исследуемый агрегат.
При описании этой составляющей на практике чаще всего используют нормальное или экспоненциальное распределение плотности вероятности.
Для нормального распределения интегральная функция и функция плотности вероятности имеют следующий вид:
где  - математическое ожидание реализации случайной величины X(t); - математическое ожидание реализации случайной величины X(t);
 - дисперсия X(t); - дисперсия X(t);
Для экспоненциального распределения плотность вероятности для случайной величины X(t) имеет следующий вид (где 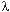 - условная плотность вероятности): Математическое ожидание:
Среднеквадратическое отклонение:
График флуктуационной и случайной составляющей сигнала представлен на рисунке:
Рис.2 - Флуктуационная и случайная составляющие сигнала
Флуктуационная составляющая несет полезную информацию об объекте. Случайная составляющая чаще всего мешает (исключение - отсутствие смазки). Поэтому, чаще всего стоит задача выделения флуктуационной составляющей на фоне шумов.
Импульсная составляющая вибросигнала характеризуется высокой скоростью нарастания, малой длительностью импульсов. Причиной импульсной составляющей являются ударные динамические явления, связанные с локальными дефектами на рабочих поверхностях элементов машины - беговых дорожках и телах качения подшипников, поверхностях соприкосновения зубьев шестерен и т.д.
Рис.3 - Вид сигнала с ударными импульсами
Спектр короткого импульса очень широкий. Т.е. энергия сигнала распределена по всему частотному диапазону, а не сосредоточена на нескольких отдельных частотах. Это характерно для недетерминированных сигналов, таких как случайный шум и переходные процессы.
Учитывая то, что спектр дельта-функции (представляющией собой импульс бесконечно малой длительности) равен бесконечности, можно математически представить ударный импульс в виде дельта-функции. Импульсная составляющая на практике чаще всего описывается с помощью дельта-функции.
Единичная импульсная функция (дельта функция) может рассматриваться как некоторый входной сигнал нулевой ширины и бесконечной высоты:
на конечной площади
Используя таблицу ключевых свойств и функций, реализуемых преобразованием Фурье, можно получить математическое описание дельта-функции в частотной области.
Если импульс повторяется с постоянной частотой, то результирующий спектр будет уже не непрерывным, а состоящим из гармоник частоты повторения импульса, а его огибающая будет совпадать с формой спектра единичного импульса. Подобные сигналы производят, например, подшипники с дефектами (выбоины, царапины и т.п.) на одном из колец. Эти импульсы могут быть очень узкими, причем они всегда вызывают появление большой серии гармоник.
Таким образом, все составляющие вибросиганала описываются математическими формулами, что дает возможность проводить анализ вибросигнала при помощи различных методов.
Структура аппаратных средств системы виброакустической диагностики
Для эффективного решения поставленных задач вибродиагностики используются аппаратные средства, имеющие различную структуру и включающие разнообразные функциональные модули.
С развитием вычислительной техники все больше задач специальной обработки ложится на средства цифровой обработки. Такие системы более просты в настройке, более стабильны во времени и проще модернизируются. Причем, эта модернизация касается прежде всего методов и алгоритмов цифровой обработки исходного сигнала. Принципиальная возможность и эффективность использования новых и традиционных методов обработки вибросигналов во многом определяется параметрами и ограничениями неизменяемой аналоговой части системы.
Рассмотрим структуру подобной системы:
Рис.4 - Функциональная схема системы виброакустической диагностики
где
- Д - датчик;
- БПО - блок предварительной обработки;
- УЗ - усилитель заряда;
- ФНЧ - фильтр нижних частот;
- БК - блок компараторов;
- У - масштабирующий усилитель;
- МБ - микропроцессорный блок;
- УВХ/ АЦП - устройство выборки-хранения/ аналогово цифровой преобразователь;
- МК - микроконтроллер;
- ОЗУ - оперативно запоминающее устройство;
- БКИ - блок клавиатуры/ индикации.
Механические колебания, генерируемые узлами механизмов распространяются по элементам машин и могут быть зарегистрированы на их поверхности. Для этого используются различные датчики (емкостные, индукционные, резистивные, электромагнитные) [ 3]. Но в последнее время наибольшее распространение получили пьезоэлектрические датчики. Это связано с тем, что пьезодатчики имеют высокую точность измерения и чувствительность, обладают высокой стойкостью и в то же время имеют миниатюрные габариты и массу. Для измерения вибраций обычно используется разновидность пьезодатчиков - пьезоакселерометры. Частотная характеристика акселерометра приведена на рисунке 5:
Рис. 5 - Частотная характеристика акселерометра
Пик характеристики соответствует частотному резонансу датчика. Ниже границ предела эффективного диапазона - низкая чувствительность и неравномерность характеристики. Выше - неравномерность характеристики и нестабильность параметров. Эффективный диапазон выбирается на центральном участке, имеющем равномерную характеристику и обуславливает стабильную работу датчика в необходимом частотном диапазоне. При монтаже датчика на объекте эффективный диапазон уменьшается в несколько раз и подъем характеристики, соотвествующий уменьшению точности работы датчика, сдвигается на более низкие частоты, поэтому при выборе датчика необходимо учитывать эту особенность характеристики.
Общепринятый подход состоит в том, что для обеспечения заданного частотного диапазона, а также погрешности преобразования около 1% необходимо чтобы резонансная частота датчика была как минимум в 2 раза выше верхнего предела рассматриваемого диапазона частот.
Сигнал пьезоэлектрического датчика - акселерометра (Д) в виде электрического заряда, пропорционального виброускорению входного сигнала, поступает на вход усилителя заряда (УЗ), который осуществляет преобразование заряда в пропорциональную величину напряжения.
Рис. 6 - Эквивалентная схема усилителя заряда
В общем случае УЗ представляет собой операционный усилитель, охваченный емкостной обратной связью (рис. 6) [ 4 ]. Кроме того, при подключении УЗ к первичному преобразователю, вырабатывающему заряд, ко входу усилителя подключаются также: емкости соединительного кабеля, первичного преобразователя (датчика), паразитная входная емкость. Амплитуда входного сигнала изменяется в широком диапазоне, поэтому необходимы средства подстройки параметров измерительного канала. Коэффициент усиления УЗ автоматически регулируется микроконтроллером (МК) таким образом, чтобы обеспечить необходимый динамический диапазон, не допуская при этом перегрузки по входному каналу.
 |
 |
 |
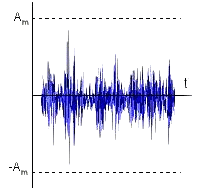
| Рис.7,а - Неполное использование динамического диапазона канала |
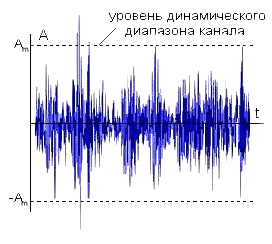
Рис.7,б - Превышение динамического диапазона, которое приводит к искажению формы сигнала |
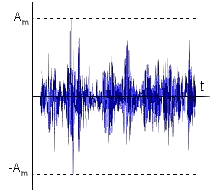
Рис.7,в - Полное использование динамического диапазона, сигнал передается без искажений |
Неполное использование динамического диапазона (рис. 7,а) приводит к увеличению влияния помех измерительного канала на результаты и неизбежное увеличение погрешности при последующем преобразовании сигнала в цифровую форму. Превышение сигналом динамического диапазона (рис. 7,б) приводит к искажению формы сигнала и потерям информации. По сути, с помощью коэффициента усиления входной сигнал нормируется так, чтобы занимать весь динамический диапазон измерительного канала и при этом сохранять исходную форму сигнала (рис. 7,в).
Если сигнал с выхода УЗ выходит за заданный диапазон, то блок компараторов (БК) сигнализирует об этом МК и он снижает коэффициент усиления УЗ до тех пор пока сигнал не будет обеспечивать полное заполнение тракта передачи. Блок компараторов представляет собой 2 компаратора, контролирующих отрицательный и положительный уровень сигнала, выходы которых подаются на RS-триггеры.
Функциональная схема БК приведена на рис.8:
Рис.8 - Функциональная схема блока компараторов
где
- К - компаратор;
- RS - RS-триггер;
- МК - микроконтроллер.
Отмасштабированный таким образом выходной сигнал УЗ поступает на фильтр нижних частот (ФНЧ), где фильтруется с целью подавления составляющих, лежащих выше необходимого диапазона частот. Этот диапазон определяется, прежде всего, информативной составляющей сигнала, которая представляет интерес для дальнейшего анализа. Коэффициент усиления данного фильтра обычно стараются привести к 1-це. Выбор и расчет ФНЧ осуществляется исходя из поставленных требований к параметрам фильтрации, точности фильтра, коэффициенту усиления и др.
Параметры, которые характеризуют фильтр, и которые необходимо контролировать при анализе:
- монотонность АЧХ (обеспечивает корректное, без пульсаций, воспроизведение сигнала в полосе пропускания фультра);
- линейность ФЧХ;
- коэффициент усиления ФНЧ: K (усиление амплитуды сигнала);
- частота среза: fс (максимальная частота, на которой фильтр пропускает сигнал без искажений, определяется затуханием a1);
- частота окончания переходной области: f1 (частота, в которой аплитуда сигнала ниже некоторой заданной амплитуды, кот. определяется допустимым затуханием в данной полосе частот - a2);
- максимальное затухание в полосе пропускания: a1;
- затухание в переходной области: a2.
Для диапазона низких частот характеристика фильтра Баттерворта наилучшим образом аппроксимирует идеальную характеристику. Хотя для частот, расположенным около точки среза и в полосе задерживания, характеристика фильтра Баттерворта заметно уступает характеристике фильтра Чебышева, имеющего немонотонную характеристику в полосе пропускания, однако ФЧХ первого лучше (более близка к линейной), чем у фильтров Чебышева, инверсных Чебышева и эллиптических сравнимого порядка. В качестве схемы реализации ФНЧ можно выбрать широко распространенную схема фильтра на ИНУН ( источник напряжения, управляемый напряжением), реализующая неинвертирующий (положительный коэффициент) усиления. Фильтр на ИНУН позволяет добиться неинвертирующего коэффициента усиления при минимальном числе элементов. Он обладает низким полным входным сопротивлением, небольшим разбросом значений элементов и возможностью получения относительно высоких значений коэффициента усиления. Кроме того, этот фильтр относительно прост в настройке. [ 5 ] 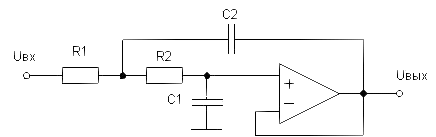
Рис. 9 - Фильтр на ИНУН второго порядка
Ослабленный после ФНЧ сигнал поступает на усилитель (У), который используется для усиления сигнала до полной загрузки динамического диапазона канала и уменьшения ошибки относительно квантования по уровню в АЦП. Коэффициент усиления усилителя устанавливается программно при помощи МК. Контроль выхода сигнала У за заданные пределы также контролируется БК, аналогично УЗ.
С выхода усилителя сигнал поступает на аналогово-цифровой преобразователь (АЦП). Для фиксации входного сигнала на время преобразования АЦП используется устройство выборки/ хранения. Оно запоминает текущую величину аналогового сигнала и держит его на выходе, пока АЦП не выдаст двоичный код (результат преобразования). С МК подается сигнал начала преобразования, а по окончании преобразования АЦП выдает сигнал о том, что выходной код готов и МК может его считывать. Большинство современных АЦП имеют встроенные УВХ.
Согласно теореме Котельникова частота дискретизации сигнала должна быть в 2 раза выше частоты самого сигнала. Поэтому, при выборе АЦП необходимо учитывать его быстродействие. Разрядность кода АЦП соответствует полному диапазону аналогового сигнала и определяет разрешающую способность кода. АЦП принципиально свойственна методическая погрешность, обусловленная заменой непрерывного аналогового сигнала дискретным сигналом.
Величина погрешности, вносимой АЦП равняется:
Клавиатура дает возможность управлять ходом анализа и получения исходных данных, а дисплей позволяет пользователю получать сообщения о параметрах записанного вибросигнала и другую информацию.
В дальнейшем будут выполнены следующие этапы:
Построение и анализ моделей преобразования вибросигналов в отдельных устройствах измерительного канала.
Формулировка рекомендаций по оптимизации параметров устройств для раных видов сигналов (гармоничный, импульсный, шумовой и их взаимодействие), что позволит, в конечном счете, с высокой точностью определить вид возникшего дефекта, сформировать прогноз его развития и снизить затраты на ремонт и восстановление агрегата.
Основные источники
-
Марпл С.Л.-мл. - Цифровой спектральный анализ и его приложения. - М: Мир, 1990. - 584 с.
Полищук Е.С. - Измерительные преобразователи. - Киев: Вища школа. Головное изд-во, 1981. - 296 с.
Техническое описание устройства УЗ-2.
Джонсон Д. Джонсон Дж. - Справочник по активным фильтрам. - М: Энергоатомиздат, 1983. - 128 с.
|