|
Медведев С.Ю., к.ф.-м.н.
"Преобразование Фурье и классический цифровой спектральный анализ"
Введение
Спектральный
анализ - один из методов обработки сигналов, который позволяет
охарактеризовать частотный состав измеряемого сигнала.
Преобразование Фурье является математической основой, которая
связывает временной или пространственный сигнал (или же некоторую
модель этого сигнала) с его представлением в частотной области.
Важную роль в спектральном анализе играют методы статистики,
поскольку сигналы, как правило, имеют случайный характер или
зашумлены при распространении или измерении. Если
бы основные статистические характеристики сигнала были точно
известны, или их можно было определить по конечному интервалу этого
сигнала, то спектральный анализ представлял бы собой отрасль "точной
науки". Однако, в действительности по отрезку сигнала можно получить
только оценку его спектра. Поэтому практика спектрального анализа -
некое ремесло (или искусство?) достаточно субъективного характера.
Различие между спектральными оценками, получаемыми в результате
обработки одного и того же отрезка сигнала разными методами, можно
объяснить различием допущений, принятых относительно данных,
различными способами усреднения и т .п. Если априори характеристики
сигнала не известны, нельзя сказать какие из оценок
лучше.
Преобразование Фурье -
математическая основа спектрального
анализа
Кратко обсудим разные виды
преобразования Фурье (более подробно см. в [1]).
Начнем с преобразования Фурье непрерывного во
времени сигнала
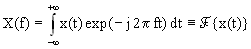 ,
(1) ,
(1)
которое идентифицирует
частоты и амплитуды тех комплексных синусоид (экспонент), на которые
разлагается некоторое произвольное
колебание.
Обратное преобразование
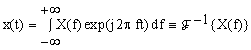 .
(2) .
(2)
Существование
прямого и обратного преобразования Фурье (которое в дальнейшем мы
будем называть непрерывно-временным преобразованием Фурье - НВПФ)
определяется рядом условий. Достаточное - абсолютная интегрируемость
сигнала
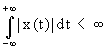 . (3) . (3)
Менее
ограничительное достаточное условие - конечность энергии
сигнала
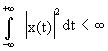 . (4) . (4)
Приведем
ряд основных свойств преобразования Фурье и функций, используемых
далее, заметив, что прямоугольное окно определяется выражением
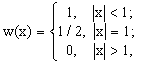 (5) (5)
а функция sinc -
выражением
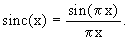 (6) (6)
Функция
отсчетов во временной области определяется выражением
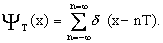 (7) (7)
Эту функцию иногда
называют также функцией периодического продолжения.
Таблица 1. Основные
свойства НВПФ и функции
|
Свойство,
функция |
Функция |
Преобразование |
| Линейность |
ag( t ) + bh( t
) |
aG( f ) + bH( f
) |
| Сдвиг по времени
|
h ( t -
t0 ) |
H( f )exp( -j2pf
t0 ) |
| Сдвиг по частоте
(модуляция) |
h ( t )exp( j2pf0
t ) |
H( f -
f0 ) |
| Масштабирование |
( 1 / |a| )h( t /
a ) |
H( af
) |
| Теорема свертки
во временной области |
g( t )*h( t
) |
G( f )H( f
)
|
| Теорема свертки в
частотной области |
g( t ) h( t
) |
G( f )*H( f
) |
| Функция
окна |
Aw( t / T
) |
2ATsinc( 2Tf
) |
| Функция
sinc |
2AFsinc( 2Ft
) |
Aw( f / F
) |
| Импульсная
функция |
Ad( t
) |
A |
| Функция
отсчетов |
 T(f) T(f) |
F F(f), F=1/T F(f), F=1/T |
Еще
одно важное свойство устанавливается теоремой Парсеваля для двух
функций g(t) и h(t):
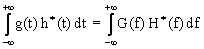 . (8) . (8)
Если
положить g(t) = h(t), то теорема Парсеваля сводится к теореме для
энергии
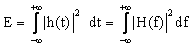 . (9) . (9)
Выражение
(9) - это, в сущности, просто формулировка закона сохранения энергии
в двух областях (временной и частотной). В (9) слева стоит полная
энергия сигнала, таким образом, функция
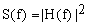 (10) (10)
описывает распределение
энергии по частоте для детерминированного сигнала h(t) и поэтому
называется спектральной плотностью энергии (СПЭ). С помощью
выражений
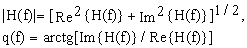 (11) (11)
можно вычислить
амплитудный и фазовый спектры сигнала h( t ).
С полным тестом статьи можно ознакомиться здесь.
|