"Разработка метода обработки изображений на основе метода нелинейной низкочастотной фильтрации с использованием нейроподобной структуры на основе преобразования Фурье".
Магистрант: Близкая О.В.
Руководитель: проф., зав. каф. АСУ, Скобцов Юрий Александрович
На сегодняшний день обработка изображений является важным направлением применения современной вычислительной техники. Известны такие задачи обработки изображений, как фильтраци я и восстановление изображений , сегментация изображений, как средства сжатия информации. Проблемы распознав а ния изображений кроме классической задачи распознавания фигур заданной формы на изображении ставят новые задачи распознавания линий и углов на изображении, распознавания края изображения.
Для решения всех перечисленных выше задач в последние годы активно используются нейросетевые алгоритмы и нейрокомпьютеры . В своей магистерской работе я также решила заниматься именно использованием нейронных сетей, как нового направления среди методов искусственного интеллекта. В последние десятилетия в мире бурно развивается новая прикладная область математики, специализирующаяся на искусственных нейронных сетях. Актуальность исследований в этом направлении подтверждается массой различных применений НС. Это автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем, организация ассоциативной памяти и многие другие приложения. С помощью НС можно, например, предсказывать показатели биржевого рынка, выполнять распознавание оптических или звуковых сигналов, создавать самообучающиеся системы, способные управлять автомашиной при парковке или синтезировать речь по тексту.
Все эти разработки используют сеть обратного распространения – наиболее успешный, по-видимому, из современных алгоритмов. Обратное распространение является систематическим методом для обучения многослойных сетей, но оно не свободно от проблем. Прежде всего нет гарантии, что сеть может быть обучена за конечное время. Много усилий, израсходованных на обучение, пропадает напрасно после затрат большого количества машинного времени. Когда это происходит, попытка обучения повторяется – без всякой уверенности, что результат окажется лучше. Нет также уверенности, что сеть обучится наилучшим возможным образом. Алгоритм обучения может попасть в «ловушку» так называемого локального минимума и будет получено худшее решение.
Разработано много других сетевых алгоритмов обучения, имеющих свои специфические преимущества. Но всё же следует подчеркнуть, что никакая из сегодняшних сетей не является панацеей, все они страдают от ограничений в своих возможностях обучаться. Для улучшения существующих сетей требуется много основательной работы. Должны быть развиты новые технологии, улучшены существующие методы и расширены теоретические основы, прежде чем данная область сможет полностью реализовать свои потенциальные возможности .
В своей магистерской работе я буду ориентироваться на язык программирования Mathlab , в частности на пакет Image Processing Toolbox . Этот пакет владеет мощными средствами для обработки изображений . Система MATLAB и пакет прикладных програм Image Processing Toolbox (IPT) является хорошим инструментом разработки, исследования и моделирования методов и алгоритмов обработки изображений. При решении задач обработки изображений этот пакет позволяет идти двумя путями. Первый из них состоит в самостоятельной программной реализации методов и алгоритмов. Другой путь позволяет моделировать решение задачи с помощью готовых функций, которые реализуют наиболее известные методы и алгоритмы обработки изображений. И тот, и другой способ оправдан. Но все же для исследователей и разработчиков методов и алгоритмов обработки изображений предпочтительным является второй путь.
В том и другом подходе объектом исследования является изображение . Я буду ориентироваться на растровые изображения, которые представляют собой двумерный массив, элементы которого (пикселы) содержат информацию о цвете. В дальнейшем, при рассмотрении методов обработки изображений, будем считать, что изображение представляется матрицей чисел (размер матрицы N*M), где значение каждого элемента отвечает определенному уровню квантования его энергетической характеристики (яркости). Это так называемая пиксельная система координат . Она применяется в большинстве функций пакета IPT.
Обработка изображений осуществляется рекурсивными и нерекурсивными методами. Рекурсивные методы используют результат обработки предыдущего пиксела, нерекурсивные - не используют. В большинстве случаев используются нерекурсивные алгоритмы обработки изображений.
Обработка изображений является многоплановой задачей. Сюда включают решение задач фильтрации шумов, геометрической коррекции, градационной коррекции, усиления локальных контрастов, резкости, восстановления изображений и др.
Одним из подходов к обработке изображения с целью улучшения его визуального качества является непосредственное использование разных фильтров. В зависимости от спецификации шумов могут применяться различные способы фильтрации: фильтры на основе преобразования Гаусса (которые используются обычно в тех случаях, когда необходимо уменьшить паразитные сигналы), полосовые фильтры с ограниченным носителем (которые предназначены для отфильтровывания верхних частот и применяются совместно с методами выделения краев изображения в задаче поиска полезной информации). Известны также алгоритмы линейной низкочастотной фильтрации, например, фильтрация скользящим средним, экспоненциальная и медианная фильтрация. Однако данные фильтры плохо подавляют мелкие, но контрастные образования, а также смазывает границу – расширяет полосу граничных точек в задаче сегментации.
В своей магистерской работе я собираюсь использовать принципиально новый подход к фильтрации, а именно применять перспективный метод нелинейной низкочастотной фильтрации с использованием нейроподобной структуры на основе преобразования Фурье.
Рассматриваемый фильтр основан на четырехслойной НС прямого распространения (рис. 1.1).
Рисунок 1.1 - Четырёхслойная нейронная сеть прямого распространения.
На входы НС подаются сигналы Х1 ,.. . , Х n с помехами. На выходе формируется отклик У1, ..., Yn без помех. Процедура фильтрации заключается в следующем. На первый слой сети поступают значения сигнала. На втором слое сети осуществляется дискретное преобразование Фурье (ПФ), в результате которого каждому нейрону второго слоя соответствует линия частотного спектра (рисунок 1.2).
Рисунок 1.2 - График 4-хслойной НС прямого распространения.
На следующем слое сети происходит непосредственно фильтрация в частотной области. Посредством синаптических весов на следующий слой формируются сигналы только тех нейронов, которые входят в полосу пропускания рассматриваемого фильтра. На посл еднем слое осуществляется обратное ПФ, которое превращает спектр в отфильтрованный сигнал. На выходе НС формируется обработанный сигнал.
Путем настройки третьего слоя можно гибко менять параметры фильтра, что позволит осуществлять кроме высокочастотной фильтрации уточнение границ, контрастирование, удаление мелких локальных образований, выравнивание освещенности. С помощью спектрального анализа исходного изображения можно выявить особенности шумов и искажений, а значит, выработать и способ борьбы с ними.
Преобразование Фурье действительной функции s(x) , заданной в пределах х от минус бесконечности до бесконечности, является комплексной величиной:
(1.1)
Полагая, что составляющие спектра S(u) существуют на частотах u в интервале от минус бесконечности до бесконечности, можно определить обратное преобразование Фурье по формуле:
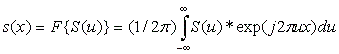 (1.2)
(1.2)
Из формулы (1.1) очевидно, что спектр действительного сигнала s(x) есть:
![]() (1.3), где:
(1.3), где:
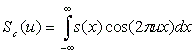 (1.4)
(1.4)
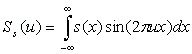 (1.5)
(1.5)
Sc(u), Ss(u) - действительная и мнимая части спектра.
При компьютерной обработке последовательности отсчётов сигнала интегральн ы е соотношения заменяют соответствующими операциями дискретного суммирования. Очевидно, что для цифрового сигнала ПФ в общем случае не может быть реализовано из-за необходимости суммирования безконечного числа членов.
Компьютерные алгоритмы ПФ дискретной последовательности отсчётов s(p) , имеющей конечную длину 0<=p<=N-1 , сводятся к вычислению конечного числа коэффициентов S(q), 0<=q<=Q-1 , согласно соотношению:
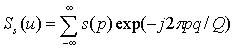 (1.6)
(1.6)
Формула (1.6) представляет собой дискретную аппроксимацию преобразования (1.1), при которой функция s(x) заменяется ступенчатой функцией s(p)=s(хp) в пределах протяжённости элемента дискретизации, где: x p =pdx (dx – шаг дискретизации ). Выражение (1.6) есть приближение, качество которого должно улучшаться при увеличении N и соответствующем уменьшении шага дискретизации dx .
В работе я также планирую заняться распознаванием двумерных контрастных изображений объектов по инвариантным информативным признакам, для реализации чего мною намечено в частности решение 3-ёх задач:
1. Формирование множества информативных признаков для распознавания, которые должны быть инвариантными как к смещению фигур в плоскости, так и к их поворотам.
2. Определение параметров НС, параметров обучающего алгоритма.
3. Проведение корректного обучения НС.
Эффективность работы системы распознавания с выбранными параметрами будет оцениваться в результате цикла статических испытаний, по результатам которых будет приниматься решение о необходимости корректирования параметров системы.
Выводы по работе и перспективы исследований
Результатом данной работы является обобщение и систематизация теоретических сведений о методах и алгоритмах обработки изображений. Был проведен научный поиск по теме "Разработка методов и алгоритмов обработки медицинских изображений с использованием методов искусственного интеллекта, проведен анализ существующих разработок в области использования нейронных сетей для этих целей, обоснована актуальность темы магистерской работы, определены направления исследования в данной области. Проанализировав существующие на сегодняшний день алгоритмы и методы обработки медицинских изображений, можно подвести итоги.
Значительная часть задач обработки информации и анализа данных связана с изображениями. Примерами могут служить обработка и анализ данных дистанционного зондирования Земли со спутников, объемные изображения объектов, полученные с помощью голографических устройств, результаты применения методов неразрушающих исследований и контроля в промышленности, разработка “органов зрения” роботов и современных медицинских систем диагностики (рентгенография, машинная томография, эндоскопия и т.д.). Для успешного решения задач поиска и идентификации объектов, определения различного рода их количественных характеристик необходимо, чтобы первичные изображения характеризовались высоким визуальным качеством, которое теряется из-за неудовлетворительных условий получения изображений, несовершенства систем передачи видеоинформации и ее отображения, влияния помех и т.п.