Нейронные сети - математический аппарат
В наши дни возрастает необходимость в системах, которые способны не только выполнять однажды запрограммированную последовательность действий над заранее определенными данными, но и способны сами анализировать вновь поступающую информацию, находить в ней закономерности, производить прогнозирование и т.д. В этой области приложений самым лучшим образом зарекомендовали себя так называемые нейронные сети -- самообучающиеся системы, имитирующие деятельность человеческого мозга. Рассмотрим подробнее структуру искусственных нейронных сетей (НС) и их применение в конкретных задачах.
Искусственный нейрон
Несмотря на большое разнообразие вариантов нейронных сетей, все они имеют общие черты. Так, все они, так же, как и мозг человека, состоят из большого числа связанных между собой однотипных элементов -- нейронов, которые имитируют нейроны головного мозга. На рис. 1 показана схема нейрона. 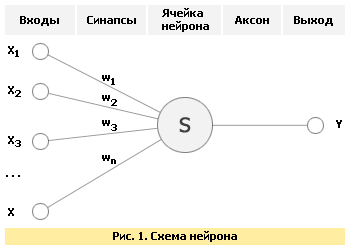 Из рисунка видно, что искусственный нейрон, так же, как и живой, состоит из синапсов, связывающих входы нейрона с ядром; ядра нейрона, которое осуществляет обработку входных сигналов и аксона, который связывает нейрон с нейронами следующего слоя. Каждый синапс имеет вес, который определяет, насколько соответствующий вход нейрона влияет на его состояние. Состояние нейрона определяется по формуле

|
(1) |
- где
- n -- число входов нейрона
- xi -- значение i-го входа нейрона
- wi -- вес i-го синапса
Затем определяется значение аксона нейрона по формуле
Где f -- некоторая функция, которая называется активационной. Наиболее часто в качестве активационной функции используется так называемый сигмоид, который имеет следующий вид:
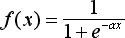
|
(3) |
Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную:
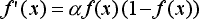
|
(4) |
При уменьшении параметра a сигмоид становится более пологим, вырождаясь в горизонтальную линию на уровне 0,5 при a=0. При увеличении a сигмоид все больше приближается к функции единичного скачка. 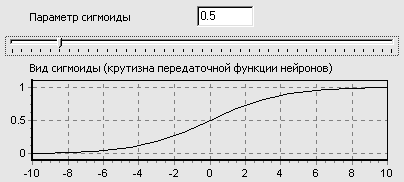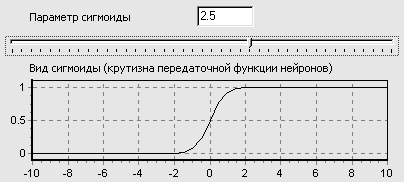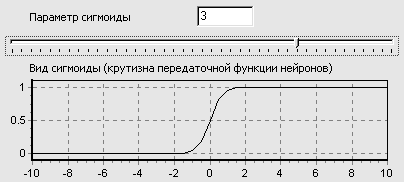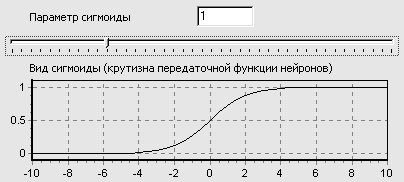
Нейронные сети обратного распространения
Нейронные сети обратного распространения -- это мощнейший инструмент поиска закономерностей, прогнозирования, качественного анализа. Такое название -- сети обратного распространения (back propagation) они получили из-за используемого алгоритма обучения, в котором ошибка распространяется от выходного слоя к входному, т. е. в направлении, противоположном направлению распространения сигнала при нормальном функционировании сети.
Нейронная сеть обратного распространения состоит из нескольких слоев нейронов, причем каждый нейрон слоя i связан с каждым нейроном слоя i+1, т. е. речь идет о полносвязной НС.
В общем случае задача обучения НС сводится к нахождению некой функциональной зависимости Y=F(X) где X -- входной, а Y -- выходной векторы. В общем случае такая задача, при ограниченном наборе входных данных, имеет бесконечное множество решений. Для ограничения пространства поиска при обучении ставится задача минимизации целевой функции ошибки НС, которая находится по методу наименьших квадратов:

|
(5) |
- где
- yj -- значение j-го выхода нейросети
- dj -- целевое значение j-го выхода
- p -- число нейронов в выходном слое
Обучение нейросети производится методом градиентного спуска, т. е. на каждой итерации изменение веса производится по формуле
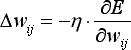
|
(6) |
где h -- параметр, определяющий скорость обучения.
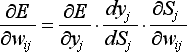
|
(7) |
- где
- yj -- значение выхода j-го нейрона
- Sj -- взвешенная сумма входных сигналов, определяемая по формуле (1).
При этом множитель
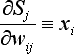
|
(8) |
- где
- xi -- значение i-го входа нейрона
Далее рассмотрим определение первого множителя формулы (7)

|
(9) |
- где
- k -- число нейронов в слое n+1.
Введем вспомогательную переменную

|
(10) |
Тогда мы сможем определить рекурсивную формулу для определения  n n-ного слоя, если нам известно  следующего (n+1)-го слоя.

|
(11) |
Нахождение же  для последнего слоя НС не представляет трудности, так как нам известен целевой вектор, т. е. вектор тех значений, которые должна выдавать НС при данном наборе входных значений.

|
(12) |
И наконец запишем формулу (6) в раскрытом виде
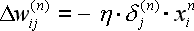
|
(13) |
Рассмотрим теперь полный алгоритм обучения нейросети:
- подать на вход НС один из требуемых образов и определить значения выходов нейронов нейросети
- рассчитать
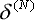 для выходного слоя НС по формуле (12) и рассчитать изменения весов для выходного слоя НС по формуле (12) и рассчитать изменения весов 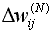 выходного слоя N по формуле (13) выходного слоя N по формуле (13)
- Рассчитать по формулам (11) и (13) соответственно
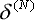 и и
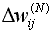 для остальных слоев НС, n = N-1..1 для остальных слоев НС, n = N-1..1
- Скорректировать все веса НС

|
(14) |
- Если ошибка существенна, то перейти на шаг 1
На этапе 2 сети поочередно в случайном порядке предъявляются вектора из обучающей последовательности.
Повышение эффективности обучения НС обратного распространения
Простейший метод градиентного спуска, рассмотренный выше, очень неэффективен в случае, когда производные по различным весам сильно отличаются. Это соответствует ситуации, когда значение функции S для некоторых нейронов близка по модулю к 1 или когда модуль некоторых весов много больше 1. В этом случае для плавного уменьшения ошибки надо выбирать очень маленькую скорость обучения, но при этом обучение может занять непозволительно много времени.
Простейшим методом усовершенствования градиентного спуска является введение момента m, когда влияние градиента на изменение весов изменяется со временем. Тогда формула (13) примет вид

|
(13.1) |
Дополнительным преимуществом от введения момента является способность алгоритма преодолевать мелкие локальные минимумы.
в начало
вернуться в библиотеку
на главную
|  Из рисунка видно, что искусственный нейрон, так же, как и живой, состоит из синапсов, связывающих входы нейрона с ядром; ядра нейрона, которое осуществляет обработку входных сигналов и аксона, который связывает нейрон с нейронами следующего слоя. Каждый синапс имеет вес, который определяет, насколько соответствующий вход нейрона влияет на его состояние. Состояние нейрона определяется по формуле
Из рисунка видно, что искусственный нейрон, так же, как и живой, состоит из синапсов, связывающих входы нейрона с ядром; ядра нейрона, которое осуществляет обработку входных сигналов и аксона, который связывает нейрон с нейронами следующего слоя. Каждый синапс имеет вес, который определяет, насколько соответствующий вход нейрона влияет на его состояние. Состояние нейрона определяется по формуле
