Автоматическое управление агрегатом синтеза.
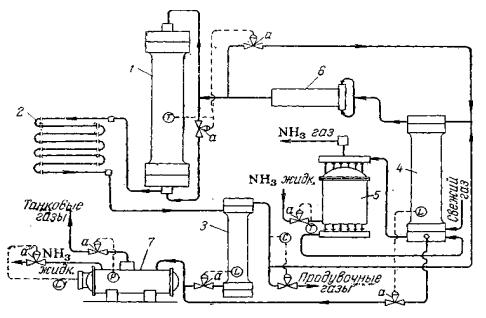
Схема агрегата с автоматическим управлением процессом синтеза аммиака показана на рис. 1. При таком управлении агрегатом автоматически регулируются следующие параметры процесса: температура в колоннах синтеза; уровни жидкого аммиака в сепараторе и конденсационной колонне; температура газа, выходящего из аммиачного конденсатора; состав циркуляционного газа по содержанию инертных примесей (СН4 и Аг); выдача жидкого аммиака из газоотделителя на склад; давление в газоотделителе. Общий принцип действия системы можно пояснить на примере автоматического регулирования температуры в колонне синтеза.
Рис. 1 Агрегат синтеза аммиака с автоматическим управлением:
1-колонна синтеза; 2-водяной конденсатор; 3-сепаратор жидкого аммиака; 4-конденсационная колонна; 5-испаритель; 6-центробежный циркуляционный компрессор; 7-газоотделитель; 8-регулирующий клапан; T-измерители температуры; L-измерители уровня; P- измеритель давления; C-регулятор состава.
Электродвижущая сила (э. д. с.), возникающая в термопаре (датчике), пропорциональна температуре, которая отсчитывается на шкале измерительного прибора. Отклонение температуры от заданной преобразуется специальным устройством в импульс давления воздуха, приводящий в действие систему регулирования. Чем больше отклонение, тем сильнее воздействие, передаваемое регулятором органу управления.
При повышении температуры открывается вентиль холодного байпаса, при снижении он прикрывается. Если этот прием регулирования не приводит к повышению температуры при закрытом байпасе, регулирование производится изменением объемной скорости. При этом регулятор начинает подавать сигнал на открытие вентиля "длинного байпаса", вследствие чего уменьшается количество газа, подаваемого в колонну циркуляционным компрессором.
Производительность колонн во многом зависит от конструкции их насадок, совершенство которых оценивается простотой и надежностью работы, а также возможностью создания наиболее благоприятного температурного режима синтеза аммиака. В идеальном случае распределение температур по высоте слоя катализатора должно соответствовать оптимальной температурной кривой. Для обеспечения оптимального режима должно быть правильно определено соотношение размеров предварительного теплообменника и катализаторной коробки и организован отвод тепла из зоны реакции таким образом, чтобы исключалась возможность как перегрева, так и переохлаждения катализатора.
Постановка задачи
Пусть имеется агрегат синтеза аммиака. Реакция в нем протекает с поглощением тепла q. Весь процесс должен удовлетворять экстремальному температурному режиму Тэ(t) реакции на внутренней поверхности стенок реактора. Управление температурой реакции будем осуществлять регулировкой потока тепла u(t) на внешней поверхности стенок. При этом процесс теплопередачи запишется в виде:
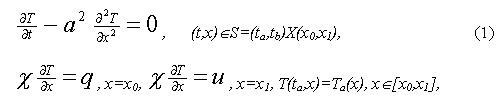
где а, c - коэффициенты температуро- и теплопроводности соответственно, Та - начальная температура стенок.
Степень отклонения температуры Т(t,x0) реакции от заданной экстремальной температуры будем оценивать функционалом
Задача оптимального управления данным реактором синтеза аммиака формулируется следующим образом. Необходимо найти поток тепла u(t), доставляющий минимум функционалу J.
Следуя градиентному подходу к задачам оптимизации систем с распределенными параметрами может быть найден градиент функционала (2):
где f(t,x) - множитель Лагранжа, удовлетворяющий сопряженной задаче:
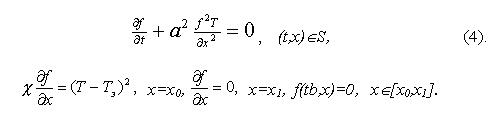
На основе градиента (3) организуется направленная итерационная коррекция управления:
где k - номер итерации, a - параметр шага градиентного спуска.
Для решения прямой и сопряженной задачи воспользуемся методом прогонки. Для построения конечно-разностного аналога дифференциального уравнения (1) используем широко известную, абсолютно устойчивую схему Кранка-Николсона:
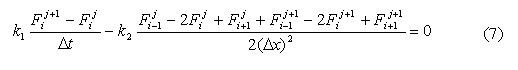
Запишем предыдущее уравнение в каноническом виде, удобном для решения методом прогонки:
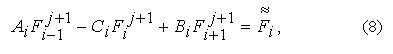
Решение системы алгебраических уравнений (8) будем искать в виде соотношения:
где коэффициенты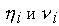 
определяются из рекуррентных соотношений:
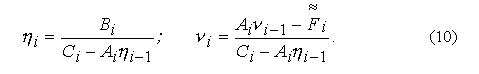
Для уравнений (8) граничные условия записываются в общем виде:
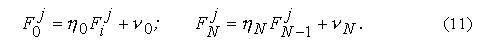
Таким образом, зная 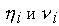и применяя формулы прямой прогонки (10),определяем все прогоночные коэффициенты 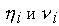. Граничное значение определяем из соотношения
Формулы (9) и (12) представляют собой формулы обратной прогонки, позволяющие определить значения Fji при всех значениях i .
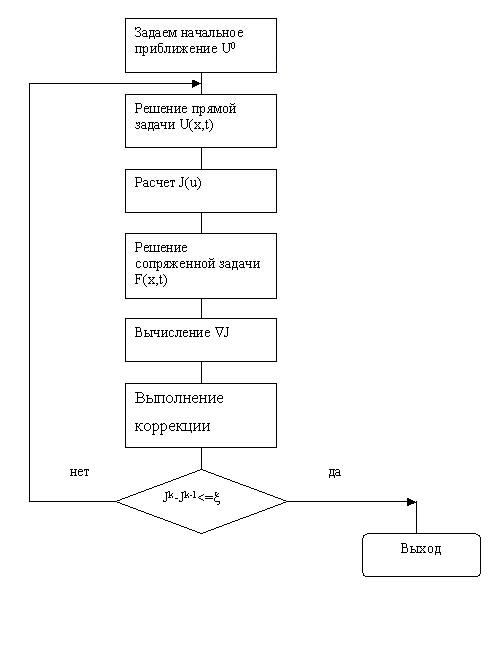
Таким образом, можно представить общий укрупненный алгоритм поставленной задачи оптимизации:
1. Володин Н.А., Толстых В.К. О применении градиентного метода оптимизации к задаче теплового управления реактором //Журн. Автоматика, 1993 г., №1, с. 40-44.
2. Кузнецов Л.Д., Дмитренко Л.М., Рабина П.Д., Соколинский Ю.А. Синтез аммиака. М.: Химия, 1982 г.
3. Демидович Б.П., Марон И.А. Численные методы анализа. М.: Наука, 1967 г.
4. Огурцов А.П., Недопекин Ф.В., Толстых В.К., Володин Н.А. Прямая оптимизация теплофизических процессов. – Донецк: Изд. "Юго-Восток", 1997 г.