(Фрагмент статьи)
( Полная версия статьи)
1.2. Постановка задачи комплексного анализа риска банкротства
1. Пусть заданы два временных интервала I и II, по которым проводится сопоставительный финансовый анализ. Пусть предприятие в каждом из периодов характеризуется набором N финансовых показателей, построенных на основании бухгалтерской отчетности за период. В периоде I это показатели Х1, … , ХN со значениями х I1, …, хIN, в периоде II — те же показатели со значениями х II1, …, хIIN, причем предполагается, что система показателей {X} достаточна для достоверного анализа (для классификации и сопоставления состояний предприятия).
2. Полное множество состояний А предприятия разбито на пять (в общем случае пересекающихся) нечетких подмножеств вида:
А1 — нечеткое подмножество состояний “предельного неблагополучия (фактического банкротства)”;
А2 — нечеткое подмножество состояний “неблагополучия”;
А3 — нечеткое подмножество состояний “среднего качества”;
А4 — нечеткое подмножество состояний “относительного благополучия”;
А5 — нечеткое подмножество состояний “предельного благополучия”.
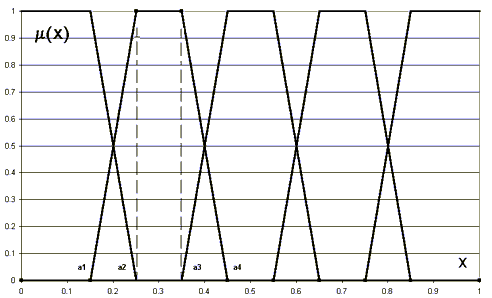
То есть терм-множество лингвистической переменной “Состояние предприятия” состоит из пяти компонентов. Каждому из подмножеств А1… А5 соответствуют свои функции принадлежности m 1(V) … m 5(V), где V — комплексный показатель финансового состояния предприятия, причем чем выше V, тем “благополучнее” состояние предприятия. Качественный вид функций m i(V) представлен на рис. 2.

Рис. 2. Качественный вид функции принадлежности
Замечание. В дальнейшем по ходу статьи мы часто будем ссылаться на вид функций принадлежности, поэтому, во избежание изобилия графиков, введем некий математический формализм, позволяющий компактное описание этих функций. Поставим в однозначное соответствие функции принадлежности m (V) нечеткое число
![]() , ( 2)
, ( 2)
где
Вернемся к комплексному показателю V. Ясно, что он функционально или алгоритмически связан с набором исходных финансовых показателей:
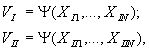 ( 3)
( 3)
но вид
3. В отношении каждого показателя
![]() , ( 4)
, ( 4)
где
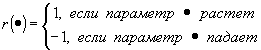 (5)
(5)
Замечание. В финансовом анализе обыкновением является то, что рост финансового показателя сопровождается
улучшением состояния предприятия (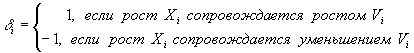 (6)
(6)
![]() = = 1).
Однако есть и исключения: например, цена обслуживания обязательств или стоимость рабочей силы. Рост этих показателей сопряжен
с ухудшением самочувствия предприятия.
= = 1).
Однако есть и исключения: например, цена обслуживания обязательств или стоимость рабочей силы. Рост этих показателей сопряжен
с ухудшением самочувствия предприятия.
4. В качестве оценки риска банкротства введем лингвистическую переменную “Степень риска банкротства” со значениями {Наивысшая, Высокая, Средняя, Низкая, Незначительная}. Взаимно однозначное соответствие лингвистических переменных “Состояние предприятия” и “Степень риска банкротства” задана табл. 1.
Таблица 1
СООТВЕТСТВИЕ ЛИНГВИСТИЧЕСКИХ ПЕРЕМЕННЫХ
“Состояние предприятия” и
“Степень риска банкротства”
|
Значение переменной “Состояние предприятия” |
Значение переменной “Степень риска банкротства” |
|
Предельное неблагополучие |
Наивысшая |
|
Неблагополучие |
Высокая |
|
Среднее качество |
Средняя |
|
Относительное благополучие |
Низкая |
|
Предельное благополучие |
Незначительная |
Тогда задача комплексного анализа может быть сформулирована следующим образом:
1. Определить процедуру
предельно благополучно с уровнем соответствия
m 1(V),относительно благополучно
с уровнем соответствия m 2(V),среднего качества
с уровнем соответствия m 3(V),неблагополучно
с уровнем соответствия m 4(V),предельно неблагополучно
с уровнем соответствия m ( (V)”.Это утверждение придает определенный вес каждой из гипотез принадлежности текущего состояния предприятия к одному из нечетких подмножеств {А}. Лицо, принимающее решение в отношении предприятия, может удовлетвориться той гипотезой, для которой значение m
(V) максимально, и таким образом для себя качественно оценить состояние фирмы.2. Определить, улучшилось или ухудшилось положение предприятия за период II по отношению к периоду I. Эта задача решается попутно с предыдущей:
если VII > VI , то состояние улучшилось,
если
VII < VI — то ухудшилось.Качественно положительная или отрицательная динамика предприятия распознается с анализом изменений значений {m }, переместился ли максимум {m } из подмножества в подмножество, и если да, то в каком направлении.
3. Оценить риск банкротства по значению показателей
VI ,VII и на основании табл. 1. С ростом значения показателя V риск банкротства снижается, и наоборот.1.3. Одно из возможных решений задачи комплексного анализа в заявленной постановке
1.3.1. Классификация значений Х
i.Пусть
D(Хi) — область определения параметра Хi, несчетное множество точек оси действительных чисел. Определим лингвистическую переменную “Уровень показателя Хi” с введением пяти нечетких подмножеств множества D(Хi):В
1 — нечеткое подмножество “очень низкий уровень показателя Хi”,В
2 — нечеткое подмножество “низкий уровень показателя Хi”,В
3 — нечеткое подмножество “средний уровень показателя Хi”,В
4 — нечеткое подмножество “высокий уровень показателя Хi”,В
5 — нечеткое подмножество “очень высокий уровень показателя Хi”.Задача описания подмножеств {В} — это задача формирования соответствующих функций принадлежности l
1-5(хi).Пример классификации
. Коэффициент автономии предприятия рассчитывается по балансу предприятия на отчетную дату и определяется формулой![]() . ( 7)
. ( 7)
Область определения Ка D(Ка
) = (0,1). Способ классификации уровня Ка , произведенного ЛПР, представлен табл. 2.Граничные значения интервалов во второй колонке табл.
2 задают абсциссы трапециевидных Т-чисел g i(a1i, a2i, a3i, a4i) ( i = 1, …, 5) вида (2). Например, подмножеству “средний уровень показателя” соответствует Т-число с координатами (0.25, 0.3, 0.45, 0.5).Таблица 2
КЛАССИФИКАЦИЯ УРОВНЯ ЗНАЧЕНИЙ КОЭФФИЦИЕНТА АВТОНОМИИ
|
Наименование показателя |
Интервал |
Классификация уровня параметра |
Степень оценочной уверенности (функция принадлежности) |
|
Ка |
0 £ Ка £ 0.1 |
“очень низкий” |
1 |
|
0 .1 < Ка < 0.2 |
“очень низкий” |
l 1 = 10 ´ (0.2 — Ка) |
|
|
“низкий” |
1— l 1 = l 2 |
||
|
0.2 £ Ка £ 0.25 |
“низкий” |
1 |
|
|
0.25 < Ка < 0.3 |
“низкий” |
l 2 = 5 ´ (0.3 — Ка) |
|
|
“средний” |
1— l 2= l 3 |
||
|
0.3 £ Ка £ 0.45 |
“средний” |
1 |
|
|
0.45 < Ка < 0.5 |
“средний” |
l 3 = 5 ´ (0.5 — Ка) |
|
|
“высокий” |
1— l 3= l 4 |
||
|
0.5 £ Ка £ 0.6 |
“высокий” |
1 |
|
|
0.6 < Ка < 0.7 |
“высокий” |
l 4 = 10 ´ (0.7 — Ка) |
|
|
“очень |
1— l 4= l 5 |
||
|
0.7 £ Ка £ 1.0 |
“очень |
1 |
Выстраивая функции принадлежности {l } (соответствующие им Т-числа {g }), эксперт руководствуется:
а) специфическими особенностями интервала анализа. То, что было типичным для 1994 года, вовсе не является таковым, скажем, для 1998 года. Так, например, в связи с несовпадением уровней инфляции, разнится стоимость обслуживания кредитов и средний вес этой стоимости в структуре текущих затрат; также разнятся оценки типичного соотношения уставного и добавленного капиталов и т.д.;
б) особенностями положения отрасли, к которой относится предприятие. Например, по данным статистики крупных акционерных компаний США и Западной Европы [17], типичным значением коэффициента автономии для текстильной промышленности является 0.40, для банков — 0.09, для ресторанов — 0.66. Указанные значения являются средними и могут быть взяты за основу при построении функций принадлежности {l }. Аналогичная статистика в России пока еще слабо представлена, а за прошедшие годы практически не публиковалась (исключение составляли крупные банки). Это серьезно осложняет работу эксперта и перемещает его внимание из области фактов Е в область интуитивных предположений S, основанных, например, на многолетнем опыте финансового анализа различных компаний;
в) особенностями положения предприятия относительно других предприятий данной отрасли (рыночная ниша, тип стратегии и т.д.). Скажем, предприятие, располагающее широкими каналами сбыта своей продукции, может гораздо увереннее пользоваться привлеченными средствами, и то невысокое значение Ка, которое является вполне приемлемым для этого предприятия, является критичным для предприятия со слабым рынком сбыта.
Таким образом, набор функций l
1-5,i по каждому параметру Хi , построенный как развернутая экспертная оценка, является эксклюзивной квалификацией предприятия, учитывающей не только специфику собственно бизнеса предприятия, но и его отраслевую принадлежность, а также специфику периода, за который проводится анализ. Переходя от значения Ка к набору {l }, соответствующему данному Ка, мы сглаживаем фактор “сезонности” при оценке параметра и тем самым создаем предпосылки для грамотного сопоставления ситуаций периодов I и II. Этот переход представлен табл. 3.Таблица 3
ПЕРЕХОД ОТ ЗНАЧЕНИЙ КА К НАБОРУ {l
}|
Наименование |
Х 1 |
,,, |
Х N |
|
Период I |
х I1 |
,,, |
х IN |
|
l 11I |
,,, |
l 1NI |
|
|
l 21I |
,,, |
l 2NI |
|
|
l 31I |
,,, |
l 3NI |
|
|
l 41I |
,,, |
l 4NI |
|
|
l 51I |
,,, |
l 5NI |
|
|
Период II |
х II1 |
,,, |
х IIN |
|
l 11II |
,,, |
l 1NII |
|
|
l 21II |
,,, |
l 2NII |
|
|
l 31II |
,,, |
l 3NII |
|
|
l 41II |
,,, |
l 4NII |
|
|
l 51II |
,,, |
l 5NII |
1.3.2. Построение функции принадлежности {m } нечетких подмножеств {À}
Анализируя опыт различных квалификаций лингвистической переменной “Состояние”, мы задаемся набором
{m }, которому отвечает пятерка нечетких Т—чисел {b } вида (2):b 1 = (0.0, 0.0, 0.15, 0,25),
b 2 = (0.15, 0.25, 0.35, 0,45),
b 3 = (0.35, 0.45, 0.55, 0,65),
b 4 = (0.55, 0.65, 0.75, 0,85),
b 5 = (0.75, 0.85, 1.0, 1,0). ( 8)
Из данного описания следует, что комплексный показатель состояния
V должен принимать значения от нуля до единицы.1.3.3. Оценка значимостей показателей для комплексной оценки
Каждому
i-му показателю в отношении каждого к-го уровня состояния предприятия можно сопоставить оценку pki значимости данного показателя для распознавания данного уровня состояния предприятия. Например, ряд банков, анализируя кредитоспособность заемщика, присваивает большую значимость показателям финансовой устойчивости и ликвидности, и меньшую — показателям прибыльности и оборачиваемости. В то же время, этот критерий не может считаться приемлемым в отношении приватизированных предприятий, ранее находящихся в собственности государства. Обыкновением для таких предприятий является то, что значительный вес основных средств в структуре активов (здания, сооружения и т.д.) соседствует с низкой рентабельностью или даже убыточностью. То есть построение системы весов pik должно проводиться по каждому предприятию строго индивидуально.Систему оценок значимостей {
p} целесообразно пронормировать следующим образом:![]() ( 9)
( 9)
Тогда, если показатели могут быть проранжированы по убыванию значимости для анализа:
Х
1 ý Х2 ý …ý ХN, ( 10)то для оценки значимостей может быть использована шкала Фишберна [7, 13]:
р
i = 2 ´ (N - i + 1)/(N ´ (N + 1)), i = 1,…,N,( 11)
которая соответствует принципу максимума наличной информационной неопределенности о значениях р
i . Если система предпочтений отсутствует, то показатели являются равнозначными, ир
i = 1/N.1.3.4. Построение показателя
VВыстроим показатели Х
i по порядку убывания значимости для анализа. Далее мы считаем, что набор функций принадлежности l 1-5,i по каждому показателю Хi построен. Этому набору отвечает система Т-чисел {g }. Получим промежуточные коэффициенты: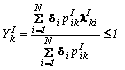 ,
,
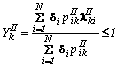 ,
, ![]() , ( 12)
, ( 12)
где d
i имеет вид (6), а pikI,II строится по схеме (11).Оптимальным способом построения
V является его согласование с выбранной системой чисел {b }. Это предполагает поиск V в нечеткой форме:![]() , ( 13)
, ( 13)
где знак “
Замечание.
Операции с нечеткими числами подробно описаны в [6, 16]. Отметим для целей настоящей работы, что линейная комбинация Т-чисел есть Т-число. Операция сложения Т-чисел, таким образом, представима совокупностью операций стандартного покомпонентного сложения действительных чисел.Переход от нечеткого числа
V к действительному виду, пригодному для использования ЛПР, можно осуществить следующим образом, используя (10):V&M = (v2 + v3)/2. ( 14)
1.3.5. Распознавание текущего состояния предприятия
Вариант 1. Принадлежность Т-числа
V одному из нечетких подмножеств {A} состояний фирмы определяется с использованием формул пересечения и объединения нечетких подмножеств. Тогда степень принадлежности состояния предприятия одному из состояний Ак определяется по формуле:![]() , ( 15)
, ( 15)
где площади определяются как соответствующие площади, ограниченные трапециевидными кривыми функций принадлежности.
Таблица 4
ПРАВИЛО РАСПОЗНАВАНИЯ ФИНАНСОВОГО СОСТОЯНИЯ ПРЕДПРИЯТИЯ
|
Наименование показателя |
Интервал значений |
Классификация уровня |
Степень |
|
V&M |
0 £ V&M £ 0.15 |
“предельное неблагополучие” |
1 |
|
0 .15 < V&M < 0.25 |
“предельное неблагополучие” |
m 1 = 10 ´ (0.25 — V&M) |
|
|
“неблагополучие” |
1— m 1 = m 2 |
||
|
0.25 £ V&M £ 0.35 |
“неблагополучие” |
1 |
|
|
0.35 < V&M < 0.45 |
“неблагополучие” |
m 2 = 10 ´ (0.45 — V&M) |
|
|
“среднего качества” |
1— m 2 = m 3 |
||
|
0.45 £ V&M £ 0.55 |
“среднего качества” |
1 |
|
|
0.55< V&M < 0.65 |
“среднего качества” |
m 3 = 10 ´ (0.65 — V&M) |
|
|
“относительное благополучие” |
1— m 3 = m 4 |
||
|
0.65 £ V&M £ 0.75 |
“относительное благополучие” |
1 |
|
|
0.75 < V&M < 0.85 |
“относительное благополучие” |
m 4 = 10 ´ (0.85 — V&M) |
|
|
“предельное благополучие” |
1— m 4 = m 5 |
||
|
0.85 £ V&M £ 1.0 |
“предельное благополучие” |
1 |
Вариант 2
. Приближенный способ распознавания, более удобный в расчетах, есть попросту определение функций m к(V&M) по виду чисел {b } (8), где V&M определяется (14). Если полученное в ходе анализа значение m к(V&M) > 0, к=1,…,5, то считаем, что состояние предприятия описывается лингвистическим значением подмножества Ак с уровнем соответствия m к(V&M). В прочих случаях принадлежности V&M другим подмножествам Ак нет. Вообще говоря, при нашем выборе системы {m } принадлежность возможна не более чем двум пересекающимся подмножествам.И тогда, с учетом (8), (13) и (14):
V&M = 0.075 ´ Y1 + 0.3 ´ Y2 + 0.5 ´ Y3 + 0.7 ´ Y4 + 0.925 ´ Y5 ( 16)
Правило для распознавания состояния предприятия, построенное на основе (8), имеет вид табл. 4. В соответствии с результатом распознавания по табл. 1 оценивается степень риска банкротства предприятия.
На этом изложение
V&M—метода анализа риска банкротства завершено.Литература
6. Кофман А., Хил Алуха Х. Введение теории нечетких множеств в управлении предприятиями, Минск: Вышэйшая школа, 1992.
14. Борисов А.Н. и др. Модели принятия решений на основе лингвистической переменной, Рига: Зинатне, 1982.
15. Борисов А.Н. и др. Принятие решений на основе нечетких моделей: Примеры использования. Рига: Зинатне, 1990.
16. Рыжов А.П. Элементы теории нечетких множеств и измерения нечеткости. М.: Диалог—МГУ, 1998.
17. Финансовый менеджмент. М.: Carana Corporation —USAID, 1998.