Сборник трудов магистрантов 2005 Донецкого национального технического университета. Выпуск 4. - Донецк, ДонНТУ Министерства образования и науки Украины, 2005.

ПРИМЕНЕНИЕ МЕТОДОВ НЕЧЕТКОЙ ЛОГИКИ В АНАЛИЗЕ ФИНАНСОВОГО СОСТОЯНИЯ ПРЕДПРИЯТИЯ

Срока Т.Б.

Донецкий национальный технический университет, кафедра АСУ

e-mail: sroka@mail.ru

Развитие предприятия и его деятельность во многом зависят от качественного анализа финансовых результатов деятельности предприятия. Анализ финансовых результатов деятельности предприятия позволяет определить наиболее рациональные способы использования ресурсов и сформировать структуру средств предприятия. Назначением финансового анализа является оценка финансовых результатов и финансового состояния предприятия, а также прогнозирование показателей предприятия и финансовой деятельности в целом.

Таким образом, видно, какую значимость имеет оценка финансового состояния предприятия, и что данная проблема является актуальной в нашей стране, при переходе к развитой рыночной экономике. В настоящее время появилось достаточно большое количество переводной и отечественной литературы на эту тему, содержащей рекомендации по расчету финансовых коэффициентов, но возникает проблема выбора определенной методики, которая соответствовала бы предприятию конкретной отрасли и условиям, в которых оно находится.

В результате анализа существующих методик оценки результатов финансовой деятельности предприятий выявлено следующее:

1) для анализа финансовой деятельности используется ряд показателей, характеризующих отдельные стороны текущего положения предприятия;

2) по ряду показателей известны некие нормативы, характеризующие их значение положительно или отрицательно, однако в большинстве случаев показатели однозначно нормировать невозможно;

3) вследствие большого количества показателей, часто изменяющихся разнонаправлено, стараются “свернуть” набор показателей в один комплексный, по значению которого можно судить о степени благополучия предприятия.

Одним из наиболее распространенных подходов к анализу финансового состояния является подход Альтмана (относящийся к методам дискриминантного анализа), результатом которого является формула

(1)

где K_i– функции показателей бухгалтерской отчетности, а α_i – полученные в результате анализа веса.

Сравнивая значение Z с пороговыми нормативами (Z₁ и Z₂), можно делать вывод о финансовом состоянии предприятия. К аналогичным моделям относятся также модели Лиса, Чессера и др. Сопоставление данных, полученных по формуле Альтмана для ряда стран, показывает, что веса в Z-свертке и пороговый интервал [Z1 , Z2] разнятся не только от страны к стране, но и от года к году в рамках одной страны (можно сопоставить выводы Альтмана о положении предприятий США за 10 лет анализа). Таким образом, подход Альтмана не обладает устойчивостью к вариациям в исходных данных. Его можно применять, когда имеется в наличии (или обосновываются модельно) однородность и репрезентативность событий, характеризующих то или иное финансовое состояние. Рассматривая отдельное предприятие, производится вероятностное описание его отношения к полной группе и не учитывается его уникальность, специфика и отличие от других.

Применение нечетко-множественного подхода к финансовому анализу предприятия является удобным в инженерном применении и обладает повышенной степенью обоснованности, поскольку в нечетко-множественный расчет попадают все возможные сценарии развития событий.

При глубоком исследовании предприятия обнаруживается больше источников неопределенности. Ряд параметров оказывается недоступным для точного измерения, и тогда в его оценке неизбежно появляется субъективный компонент, выражаемый нечеткими оценками типа "высокий", "низкий", "наиболее предпочтительный", "весьма ожидаемый", "скорее всего", "маловероятно", "не слишком" и т.д. Появляется то, что в науке описывается как лингвистическая переменная со своим терм-множеством значений, а связь количественного значения некоторого фактора с его качественным лингвистическим описанием задается так называемыми функциями принадлежности фактора нечеткому множеству. Функции принадлежности параметров нечетким множествам являются количественной мерой наличной информационной неопределенности в отношении анализируемых параметров, значение которых описывается в лингвистически нечеткой форме.

1. Введем следующие базовые множества и подмножества состояний, описанные на естественном языке.

Полное множество состояний Е предприятия разбито на пять (в общем случае пересекающихся) нечетких подмножеств вида:

E₁ - подмножество состояний "предельного неблагополучия";

E₂ - подмножество состояний "неблагополучия";

E₃ - подмножество состояний "среднего качества";

E₄ - подмножество состояний "относительного благополучия";

E₅ - подмножество состояний "предельного благополучия".

То есть терм-множество лингвистической переменной “Состояние предприятия” состоит из пяти компонентов. Каждому значению лингвистической переменной Е₁… Е₅(которое является нечетким подмножеством значений интервала (0,1)) соответствуют свои функции принадлежности m₁(х) … m₅(х). Общеупотребительными в этом случае являются трапециевидные функции принадлежности. Качественный вид функций m _i(х) представлен на рис. 1.

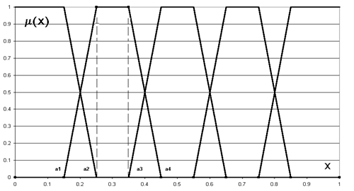
Рис. 1. Качественный вид функции принадлежности

Верхнее основание трапеции соответствует полной уверенности эксперта в правильности своей классификации, а нижнее – уверенности в том, что никакие другие значения интервала (0,1) не попадают в выбранное нечеткое подмножество.

Поставим в однозначное соответствие функции принадлежности m (х) трапециевидное число

, ( 2)

где и - абсциссы нижнего основания, а и - абсциссы верхнего основания трапеции (рис. 1), задающей m в области с ненулевой принадлежностью носителя х соответствующему нечеткому подмножеству.

Соответствующее множеству E полное множество степеней риска банкротства G разбивается на 5 подмножеств:

G₁ - подмножество "предельный риск банкротства",

G₂ - подмножество "степень риска банкротства высокая",

G₃ - подмножество " степень риска банкротства средняя",

G₄ - подмножество " низкая степень риска банкротства ",

G₅ - подмножество "риск банкротства незначителен".

Здесь и далее предполагаем, что показатель G принимает значения от нуля до единицы по определению.

Для произвольного отдельного финансового или управленческого показателя Х_i полное множество его значений В_i разбивается на пять подмножеств:

B_i1 - подмножество "очень низкий уровень показателя Х_i",

B_i2- подмножество "низкий уровень показателя Х_i",

B_i3 - подмножество "средний уровень показателя Х_i",

B_i4 - подмножество "высокий уровень показателя Х_i",

B_i5- подмножество "очень высокий уровень показателя Х_i".

Причем здесь и далее по умолчанию предполагаем:

1. Рост отдельного показателя Х_i сопряжен со снижением степени риска банкротства с улучшением самочувствия рассматриваемого предприятия. Если для данного показателя наблюдается противоположная тенденция, то в анализе его следует заменить сопряженным.

2. Выполняется дополнительное условие соответствия множеств B, Е и G следующего вида: если все показатели в ходе анализа обладают, в соответствии с классификацией, уровнем подмножества B_ij, то состояние предприятия квалифицируется как E_j , а степень риска банкротства – как G_j. Выполнение этого условие влияет, с одной стороны, на правильную количественную классификацию уровней показателей (см. далее этап 5 метода) и на правильное определение уровня значимости показателя в системе оценки (см. далее этап 3 метода).

2. Построим набор отдельных показателей X={Х_i}общим числом N, которые, по мнению эксперта-аналитика, с одной стороны, влияют на оценку риска банкротства предприятия, а, с другой стороны, оценивают различные по природе стороны деловой и финансовой жизни предприятия (во избежание дублирования показателей с точки зрения их значимости для анализа).

3. Сопоставим каждому показателюХ_i уровень его значимости для анализа r_i. Чтобы оценить этот уровень, нужно расположить все показатели по порядку убывания значимости так, чтобы выполнялось правило

. (3)

Если система показателей проранжирована в порядке убывания их значимости, то значимость i-го показателя r_i следует определять по правилу Фишберна:

. (4)

Правило Фишберна отражает тот факт, что об уровне значимости показателей неизвестно ничего кроме (3). Тогда оценка (4) отвечает максиму энтропии наличной информационной неопределенности об объекте исследования.

Если же все показатели обладают равной значимостью (равнопредпочтительны или системы предпочтений нет), тогда

r_i = 1/N. (5)

4. Построим классификацию текущего значения g показателя степени риска как критерий разбиения этого множества на нечеткие подмножества (таблица 1):

Таблица 1

Интервал значений g	Классификация уровня параметра	Степень оценочной уверенности (функция принадлежности)
0 £ g£ 0.15	G₅	1
0 .15 < g < 0.25	G₅	m₅ = 10 ´ (0.25 - g)
0 .15 < g < 0.25	G₄	1- m₅ = m₄
0.25 £ g £ 0.35	G₄	1
0.35 < g < 0.45	G₄	m₄ = 10 ´ (0.45 - g)
0.35 < g < 0.45	G₃	1- m₄ = m₃
0.45 £ g £ 0.55	G₃	1
0.55< g < 0.65	G₃	m₃ = 10 ´ (0.65 - g)
0.55< g < 0.65	G₂	1- m₃ = m₂
0.65 £ g £ 0.75	G₂	1
0.75 < g < 0.85	G₂	m₂ = 10 ´ (0.85 - g)
0.75 < g < 0.85	G₁	1- m₂ = m₁
0.85 £ g £ 1.0	G₁	1

5. Построим классификацию текущих значений x показателей Х как критерий разбиения полного множества их значений на нечеткие подмножества вида В.

Таблица 2

Наименование показателя	Критерий разбиения по подмножествам
Наименование показателя	В_i1	В_i2	В_i3	В_i4	В_i5
Х₁	x₁<b₁₁	b₁₁< x₁<b₁₂	b₁₂< x₁<b₁₃	b₁₃< x₁<b₁₄	b₁₄< x₁
…	…	…	…	…	…
Х_i	x_i<b_i1	b_i1< x_i<b_i2	b_i2< x_i<b_i3	b_i3< x_i<b_i4	b_i4< x_i
…	…	…	…	…	…
Х_N	x_N<b_N1	b_N1< x_N<b_N2	b_N2< x_N<b_N3	b_N3< x_N<b_N4	b_N4< x_N

6. Произведем оценку текущего уровня показателей и сведем полученные результаты в таблицу 3.

Таблица 3

Наименование показателя	Текущее значение
Х₁	х₁
…	…
Х_i	х_i
…	…
Х_N	х_N

7. Проведем классификацию текущих значений х по критерию таблицы вида 2. Результатом проведенной классификации является таблица 4, где l_ij – уровень принадлежности носителя х_i нечеткому подмножеству В_j.

Таблица 4

Наименование показателя	Результат классификации по подмножествам
Наименование показателя	В_i1	В_i2	В_i3	В_i4	В_i5
Х₁	l₁₁	l₁₂	l₁₃	l₁₄	l₁₅
…	…	…	…	…	…

8. Теперь выполним формальные арифметические действия по оценке степени риска банкротства g:

, (6)

где

, (7)

l_ij определяется по таблице 4, а r_i – по формуле (4) или (5).

Существо формул (6) и (7) состоит в следующем. Первоначально мы оцениваем веса того или иного подмножества из B в оценке состояния предприятия Е и в оценке степени риска G (внутреннее суммирование в (6)). Эти веса в последующем участвуют во внешнем суммировании для определения среднего значения показателя g, где g_j есть не что иное как средняя оценка g из соответствующего диапазона таблицы 1.

9. Классифицируем полученное значение степени риска на базе данных таблицы 1. Результатом классификации являются лингвистическое описание степени риска банкротства и (дополнительно) степень уверенности эксперта в правильности его классификации. И тем самым наш вывод о степени риска предприятия приобретает не только лингвистическую форму, но и характеристику качества наших утверждений.

Основным недостатком рассмотренного метода является участие эксперта при выборе системы показателей и определении их уровня значимости.

Для устранения этого недостатка предлагается:

Используя данные бухгалтерской отчетности (баланс) определяются основные финансовые коэффициенты за несколько отчетных периодов (месяц, квартал).
Определяется корреляционная взаимосвязь между финансовыми коэффициентами.
Производится группировка финансовых коэффициентов. При этом значительные показатели коэффициентов корреляции (>0,7) свидетельствуют о высокой взаимосвязи между финансовыми коэффициентами, т.е. о возможном дублировании информации, характеризующей финансовое состояние предприятия. Чем меньше значение коэффициента корреляции, тем меньше связь между показателями. Следовательно, набор из таких коэффициентов может характеризовать финансовое состояние предприятие более подробно с различных сторон.
Для определения уровня значимости показателей, выбранных для проведения анализа, можно использовать один из методов факторного анализа.

В результате описанной процедуры можно получить более объективную систему показателей и их уровней значимости, чем при их определении экспертом, а следовательно повысить точность оценки финансового состояния. Кроме этого предложенную процедуру можно применять к любому количеству показателей, в то время как эксперт с ростом количества показателей с меньшей степенью уверенности может выбрать необходимые из них и, тем более, оценить их значимость.

Для реализации предложенного подхода необходимо большое количество данных бухгалтерской отчетности за длительный период времени (желательно несколько лет). Предлагается для расчета и хранения показателей за длительный период использовать хранилище данных.

Список литературы

1. Недосекин А.О., Максимов О.Б. Новый комплексный показатель оценки финансового состояния предприятия.

Altman E.I. personal Internet homepage. – On site: http://pages.stern.nyu.edu/~ealtman/index.html.
Давыдова Г.В., Беликов А.Ю. Методика количественной оценки риска банкротства предприятий // Управление риском, 1999 г., № 3, с. 13-20. - Также на сайте: http://sedok.narod.ru/s_files/irkutsk.htm .

10.html